单压下有序多裂隙脆性材料破坏机制及其简化模型

曹 平，蒲成志

(中南大学 资源与安全工程学院，长沙 410083)

单压下有序多裂隙脆性材料破坏机制及其简化模型

曹 平，蒲成志

(中南大学 资源与安全工程学院，长沙 410083)

采用试件养护前期拔出预埋插片形成预制裂隙的方法制作多裂隙脆性材料试件，并在伺服控制单轴加载系统上对其进行加载试验。基于单压下脆性材料局部破损的应变软化机理建立裂隙体数值模型，对比试验与数值计算结果分析有序多裂隙脆性材料破坏机制及其影响因素。结果表明：除裂隙倾角及其几何排布外，裂隙在试件中的相对分布位置也影响裂隙体的破坏特征，且影响程度与裂隙面上有效剪切力大小有关，有效剪切力越大，则影响越显著。试验与数值计算结果显示：多裂隙试件中存在一组优势破坏面，与和裂隙走向相一致的试件斜对角线重合，裂隙分布在优势破坏面上或附近时，其尖端发育微裂纹的机率大于远离优势破坏面位置裂隙。结合有序多裂隙试件破坏特征及数值模型单元屈服状态，提出2种近置裂隙尖端裂纹发育简化模型，并结合本试验结果验证了简化模型的可行性。

脆性材料；有序多裂隙；破坏机制；简化模型；优势破坏面；应变软化

对于颗粒体之间有胶结的脆性材料，颗粒间胶结力的丧失是造成材料破坏的主要原因。具有初始宏观倾斜裂隙的这类材料，在单向压应力作用下，由于裂隙面上压剪应力的存在而在裂隙尖端邻域内产生应力集中现象，并在最大拉应力方向上诱发材料损伤破坏。实验表明[1]，裂隙尖端宏观微裂纹发育瞬时，材料的强度达到最大值，虽然需要继续加载来维持微裂纹的不稳定扩展，但是试件强度明显弱化；沈珠江[2]认为，这类材料的强度弱化是由胶结块间的软弱带破损软化引起的，并引入代偿应变取代损伤应变，提出了能够描述含初始缺陷颗粒体材料软化现象的二元介质模型，建立了破损力学的基本框架[2-4]。

断裂力学认为，应力集中现象仅仅表现在裂隙尖端的微小邻域内。黎立云等[5]的研究结果表明：初始宏观裂隙间距为一倍裂隙长度时，裂隙尖端应力场的叠加效应开始显现；裂隙无限接近时，应力场的叠加将趋于无穷大；结合有限元数值计算结果，给出了裂隙间应力场叠加的数值解。黄明利等[6]结合 RFPA2D分析软件探讨了不同几何排布近置多裂隙应力场4种叠加模式，讨论了裂纹几何排布对应力场叠加规律的影响。已有研究表明[7-9]，在裂隙几何排布相同时，裂隙尖端发育微裂纹的机会与尖端应力场的叠加效应均等，且与裂隙在试件上的相对分布位置无关。李银平等[10]基于经典 Kachanov方法，将裂纹面伪面力重新分解，提出能够解决裂隙间强相互作用的渐进分析方法，并取得良好的精度。但是实验发现：在裂隙几何排布相同时，裂隙尖端发育微裂纹的机会并不均等，还受到裂隙在裂隙体上相对分布位置的影响。本文作者认为，已有研究成果均是建立在无限大假设基础上得到的，但是实验所用试件为有限边界，这是造成实验现象与理论预测差异的主要原因。本文作者基于这一认识，结合含裂隙类岩材料的断裂实验，并基于FLAC3D应变软化本构模型，建立了有序分布多裂隙数值模型，探讨有限边界下脆性材料多裂隙体的破坏机制，并验证裂隙相对分布位置对裂隙体破坏模式影响的存在。最后结合有序多裂隙试件破坏特征及数值模型单元屈服状态，提出2种近置裂隙尖端裂纹发育简化模型，并给出2种简化模型的理论解。

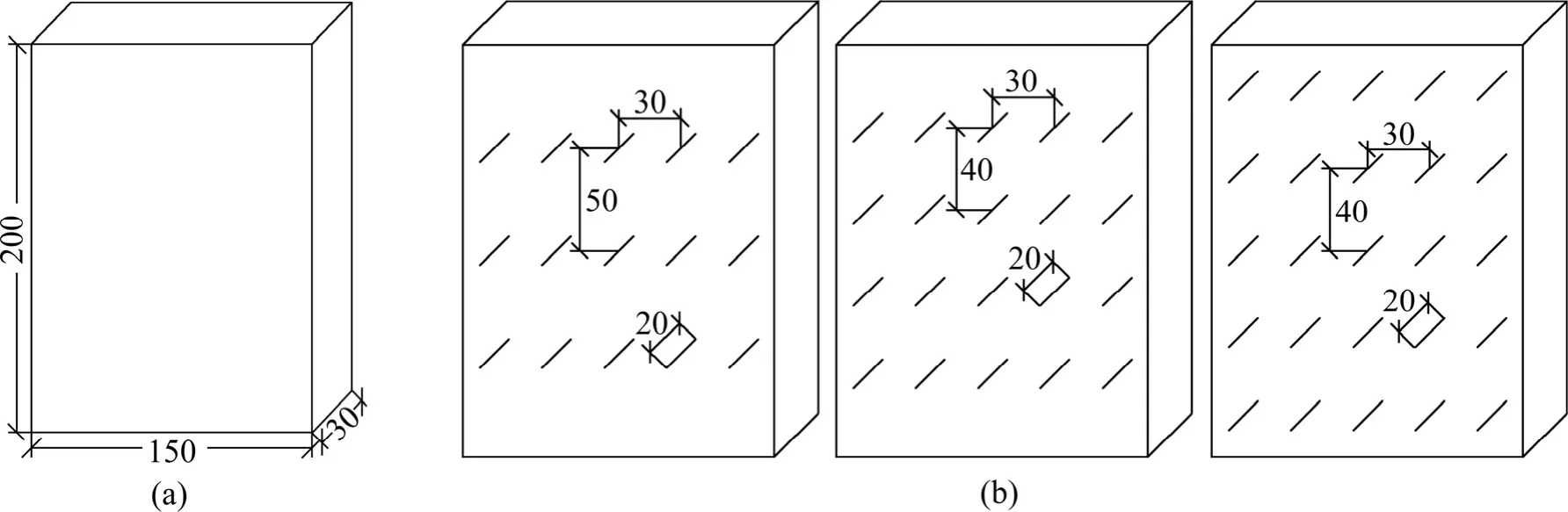
图1 试件外形尺寸和试件裂隙分布特征Fig.1 External measurement of specimens (a) and fissure distribution state on specimen (b) (Taking fissure inclination angle being 45° for example) (mm)

1 有序多裂隙试件破坏实验

1.1 试件制作与加载

试件采用标号425的白水泥、自来水和经1.05 mm孔径筛分过的细沙按体积比 2:1:1制作，外形尺寸(高×宽×厚)为200 mm×150 mm×30 mm；采用试件中预埋0.4 mm厚的铝合金片预制贯通裂隙，并在试样养护24 h后拔出铝合金片，预制裂隙长度为20 mm。预制裂隙倾角α为 25°和 45°，每个角度下分别预制15条、20条和25条有序贯通裂隙(每5条一排)。试件中裂隙布置方式如图1所示。

实验加载装置为高精度能控制加载速度的电液伺服控制试验机，配合 DCS-200加载控制系统，在200N/S的力控加载速度下，观察并拍摄试件加载过程中裂隙尖端微裂纹的起裂、扩展及贯通过程。实验过程中，在试件上下受压端与机头钢块之间布置预先涂抹黄油的橡皮垫，以减弱端部效应的影响。

1.2 有序多裂隙试件破坏模式

蒲成志[11]在系列实验中发现：裂隙倾角是影响试件破坏特征的主要因素，并基于滑动裂纹模型，给出理论上的解释，得到预制裂隙倾角在某个角度(25°)时，裂隙体取得强度最小值。但是进一步分析裂隙体破坏模式发现：在预制裂隙特征相同，裂隙间距大于一倍裂隙长度，且同一试件中裂隙几何排布相同时，尖端发育微裂纹并不是理论预测的机会均等，而是存在一个优势破坏面，在优势破坏面上预制裂隙尖端发育微裂纹且相互贯通的机率较高；这一破坏特征在预制裂隙倾角为 25°时尤其明显，45°倾角时，仅在 25条裂隙体中显著具有此类破坏特征，根据滑动裂纹模型理论，这是由于 25°倾角时裂隙面上的有效剪应力大于45°倾角裂隙体所致。

图2～4所示为不同裂隙分布特征试件破坏模式。由图2可看出，15条预制裂隙试件发生破坏时，试件两侧裂隙尖端均有微裂纹发育，这是由加载时试件两端与压头间残余端部效应引起的。25°倾角时，4号、3号与2号裂隙与两侧裂隙尖端几乎同时发育微裂纹，并很快搭接、贯通，形成一条贯通的破坏面，本文作者称其为优势破坏面，破坏面上以拉伸破坏形态为主；45°倾角时，位于这一优势破坏面上的裂隙尖端并没有发育微裂纹，而只是在试件两侧裂隙尖端显著发育翼形裂纹。这一实验现象表明：45°倾角时裂隙面上有效剪切力不足以诱发近置裂隙尖端发生微裂纹贯通，仅能在少数裂隙尖端诱发最大周向正应力方向上的翼形裂纹。

图2 15条预制裂隙试件尖端微裂纹发育模式Fig.2 Characteristics of micro-cracks appeared at fissure tips of specimens with 15 fissures: (a) 25°; (b) 45°

由图3可看出，20条预制裂隙试件发生破坏时，同样由于残余端部效应的影响，在试件两侧裂隙尖端有少量微裂隙发育，但是并没有形成贯通破坏面，而在裂隙体优势破坏面走向上的裂隙尖端出现微裂纹搭接、贯通现象，尤其在25°倾角时表现尤为显著：5号、4号、3号与2号裂隙尖端微裂纹虽迟于右侧裂隙尖端微裂纹发育，但其扩展速率很快，并率先形成贯通破坏面；45°倾角时，试件右侧裂隙尖端同样优先发育微裂隙，在其尚未贯通时，3号、2号与1号裂隙尖端微裂纹发育并迅速搭接，5号与4号裂隙岩桥间也出现剪切贯通裂纹，而3条4号裂隙间则是由翼裂纹搭接贯通，与 25°倾角裂隙体相比，岩桥区发育拉剪破坏显得比较困难，而是以剪切破坏为主，并呈现出与尖端翼形裂纹发育的均等态势。

图3 20条预制裂隙试件尖端微裂纹发育模式Fig.3 Characteristics of micro-cracks appeared at fissure tips of specimens with 20 fissures: (a) 25°; (b) 45°

由图4可看出，25条预制裂隙试件发生破坏时，两侧裂隙尖端没有微裂纹发育，位于优势破坏面上的5号、4号、3号、2号与1号裂隙尖端优先发育微裂纹，并很快搭接、贯通，最终导致试件破坏。25°倾角时，裂隙尖端发育拉剪复合型微裂纹；45°倾角时，裂隙尖端发育由剪应力诱发的次生共面裂纹。

图4 25条预制裂隙试件尖端微裂纹发育模式Fig.4 Characteristics of micro-cracks appeared at fissure tips of specimens with 25 fissures: (a) 25°; (b) 45°

根据图1所示裂隙体预制裂隙几何排布特征， 20条与 25条预制裂隙试件中倾角相同的预制裂隙几何排布特征相同：裂隙排距与岩桥倾角及长度一致。根据断裂力学和已有研究结论，理论上2种试件应该具有相似破坏特征，但是图3与图4所示试件破坏模式并不一致：图3中优势破坏面上预制裂隙尖端发育微裂纹的同时，试件右侧也有微裂纹发育。而图4中只有优势破坏面上的预制裂隙尖端有微裂纹发育；45°倾角时差异性更加明显。这一实验现象表明：在裂隙几何排布相同时，裂隙在试件上的分布特征也影响着裂隙体试件的破坏规律。

2 裂隙尖端应力场

由线弹性断裂力学理论可知，作用在裂隙面上的垂直正应力对裂隙的相对滑动没有贡献，裂隙尖端的应力集中主要由裂隙面上的剪应力产生。因此，压剪裂纹的破坏是由于裂隙面上的剪切应力引起的。考虑裂隙闭合效应的影响，设裂隙面摩擦因数为f，根据弹性力学求得平面问题中裂隙面上的有效剪应力(effτ)为

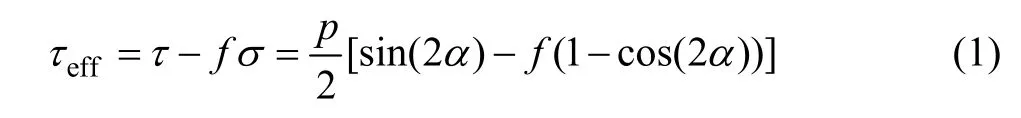
式中：σ为预制裂隙表面正应力；τ为预制裂隙表面剪应力；α为预制裂隙倾角；p为裂隙体端部均布压力。

根据线弹性断裂力学理论，受剪切应力作用时裂隙尖端领域应力场如图5所示。

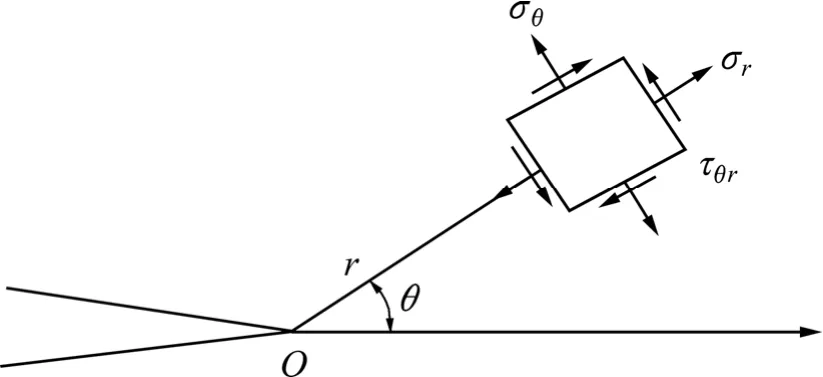
图5 裂隙尖端应力场Fig.5 Stress fields of fissure tip

在以裂尖为坐标原点的极坐标系中，点位(r, θ)处的正应力σθ可表示为

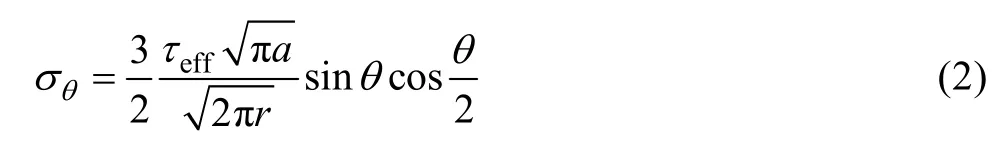
式中：a为裂隙半长度。

最大周向正应力理论认为裂隙尖端初始裂纹将沿周向最大正应力方向扩展，因此，对式(2)中关于角θ求偏微分，并令其为0，如下式：

由式(3)可求得 θ=70.5°，即理论上翼形裂纹起裂角为70.5°。

根据式(2)，并结合线弹性断裂力学中关于应力强度因子(KI)的定义，得到由最大周向应力理论确定的在裂隙尖端邻域各开裂角度下的KI表达式[12]：

大量实验结果和理论计算表明：压剪应力作用下无限大板单裂隙尖端翼形裂纹起裂角接近 70°，其扩展方向朝最大主应力方向弯折；但是在近置多裂隙体内，最大周向应力仅能判定翼形裂纹起裂，在判定裂纹扩展路径上则与实验测得结果偏差较大。研究结果表明[13]，裂隙尖端发育何种裂纹、岩桥发生何种破坏模式除了受微裂纹起裂形态影响外，还与近置裂纹的相对分布状态有关，并据此衍生出拉伸破坏、剪切破坏和拉剪复合破坏3种模式；本次试验也验证了这一结论：25°倾角时，裂隙体多以拉剪复合型破坏为主，45°时受岩桥长度的影响，分别呈现翼裂纹拉伸破坏和次生共面裂纹剪切破坏模式。因此，对近置多裂隙脆性材料在力学作用下的相应机制仍需进行大量的研究工作。

3 裂隙体应变软化模型

岩体在单向应力作用下与三向应力作用下的破坏特征具有一个显著的差别：单向应力下岩体呈现局部材料破坏失稳的脆性破坏特征，三向应力下岩体呈现整体破坏失稳的延性破坏特征。材料发生局部破损的脆性破坏时，大部分岩体结构仍是完好的，只是在局部破损面上发生剪切或拉伸屈服现象，这种脆性材料变形破坏的局部化，等效于屈服破坏面上材料的应变软化。而对于颗粒体之间有胶结的脆性材料，其软化与颗粒体胶结力的丧失有关。

HUTCHINSON[14]认为，微裂纹的出现引起局部材料刚度的下降，使得微裂纹附近残余应力被释放，从而导致宏观裂纹尖端应力场的再分布。微裂纹的出现导致的材料刚度下降，表现为裂纹破坏面上材料的应变软化。陈蕴生等[15]在CT扫描技术下进行了内置裂隙扩展实验，发现试件的破坏是由裂隙的损伤演化引起的，裂隙尖端的扩展是造成试件断裂的主要发源地；笔者实验中也发现，试件的破坏始于裂隙尖端微裂纹的发育，终于微裂纹的贯通，微裂纹贯通后，虽然贯通面上颗粒体的摩擦增强作用可以维持试件残余强度的存在，但是试件本身已经丧失承载能力。

为了探究多裂隙体中裂隙尖端微裂纹在力学作用下的力学响应规律，深入分析影响多裂隙体破坏机制的因素，本文作者基于有限差分理论建立了考虑应变软化机制的裂隙体数值模型，并根据实验条件及裂隙体材料力学参数(见表1)进行计算，分析数值条件下多裂隙试件的破坏贯通机制。裂隙体试件贯通破坏面上材料应变软化速率列于表2，边界条件如图6所示；加载速率为9×10-8m/step。

表1 数值模型参数统计表Table1 Statistical Tableof parameters for numerical models

表2 数值模型贯通破坏面软化参数Table2 Softening parameters of numerical models

图6 数值模型与边界条件示意图Fig.6 Sketch of numerical model and boundary condition

4 裂隙体屈服状态及其应力演化规律

4.1 裂隙体模型单元屈服状态

图7～9所示为不同裂隙几何分布特征数值模型单元屈服状态。图7所示为15条裂隙体模型失稳时屈服状态。对比图2发现：25°倾角裂隙体屈服是由优势破坏面走向上岩桥发生拉剪复合破坏引起的，并在较多裂隙尖端出现，同时伴有同排裂隙间压减屈服破坏出现；45°倾角裂隙体模型发生屈服破坏时，裂隙破坏模式较混乱，这是由于裂隙面上有效剪应力减弱，导致优势破坏面上裂隙尖端发育微裂纹(单元屈服)的优势减弱引起的。

图8所示为20条裂隙体模型失稳时屈服状态。对比图7发现，模型单元屈服规律性有所提高，尤其是在25°倾角条件下。对比图3发现，25°倾角时，实验中试件呈现出一条优势破坏面，而数值模型中分布有两条，考虑到实验中边界条件的差异性(残余端部效应的存在及模型尺寸误差)及实验结果的随机性，两条优势破坏面总体上具有相同的特征；由于裂隙面上有效剪切力的减弱，45°倾角裂隙体模型单元屈服规律较差。

图9所示为25条裂隙体模型失稳时屈服状态。对比图4发现：25°倾角裂隙体屈服是由优势破坏面走向上岩桥发生拉剪复合破坏引起的，虽然图 1显示 20与25条裂隙试件中岩桥具有相同的几何特征，但是由于 20条裂隙时优势破坏面上的裂隙分布具有两条相同的潜在优势面，实验测得(见图3)优势破坏面与其中一条重合，数值计算显示(见图8)在两条潜在优势面间发生了台阶状过渡破坏模式；25条裂隙试件有唯一确定的潜在优势面，实验与数值计算结果相吻合。在45°倾角条件下，由于45°倾角裂隙面上有效剪应力减弱导致的优势破坏面“优势”减小，在贯通破坏面上方另有一条贯通的、具有与优势破坏面相同走向的屈服面。

4.2 裂隙尖端微裂纹发育规律及其力学行为

实验发现：裂隙尖端发育典型翼裂纹时，翼裂纹起裂部位往往并不位于裂隙尖端，而是在距离尖端一定距离处位置发育，如图10所示。

对比数值模型的应力场分布形态，如图11所示，拉应力场并没有出现在裂隙尖端，而是起始于尖端后面一个网格，在这一个网格长度范围内，应力场由拉应力逐渐过渡到尖端的最大压应力，应力场这一分布特征与实验结果相吻合。

裂隙体发生拉剪复合破坏模式时，微裂纹则起始于裂隙尖端，并有部分微裂纹在裂隙走向上发育一定长度后才发生拐折，如图12所示，但是裂隙尖端微裂纹起裂后，翼形裂纹拐折向最大主应力方向发育的特征不明显，更多呈现出近直线贯通模式。

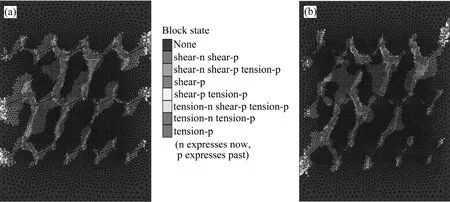
图7 15条裂隙体模型屈服状态Fig.7 Yielding characteristics of fissure-body models with 15 fissures: (a) 25°; (b) 45°

图8 20条裂隙体模型屈服状态Fig.8 Yielding characteristics of fissure-body models with 20 fissures: (a) 25°; (b) 45°

图9 25条裂隙体模型屈服状态Fig.9 Yielding characteristics of fissure-body models with 25 fissures: (a) 25°; (b) 45°

图10 典型翼裂纹发育形态Fig.10 Spatial morphologies of typical wing-cracks: (a) 45°;(b) 25°

图11 裂隙尖端第一主应力分布形态Fig.11 Distribution of first main stress at fissure tip

图12 拉剪复合破坏裂纹发育形态Fig.12 Spatial morphologies of micro-cracks under tensileshear comprehensive stresses: (a) 15 fissures; (b) 20 fissures

图13 岩桥区单元屈服状态Fig.13 Yield situation of grid cell in rock-bridge

由图13可看出，岩桥区网格单元发生拉剪复合破坏模式，这表明屈服网格单元上不仅作用诱发翼形裂纹的拉应力，还有剪应力存在。由于岩桥区内斜向45°方向上最大剪应力的存在，使得初始微裂纹后续扩展过程中，受到拉剪复合应力控制，本文作者认为，这是影响近置多裂隙破坏进程的主要原因，岩桥区上剪应力的存在，使得实验观察到的内凹形翼形裂纹(见图10)扩展模式很难出现，较多地呈现出外凸扩展、或直线剪切破坏模式(见图12)。

对于 45°倾角裂隙体试件，其岩桥区以剪切破坏为主，剪切带方向与裂隙几乎平行。

综上所述，近置多裂隙脆性材料发生裂隙贯通破坏时，岩桥区较多呈现拉伸破坏、拉剪复合破坏和剪切破坏3种模式，其中拉伸破坏与拉剪符合破坏均以尖端周向正应力为主导因素。结合多裂隙试件破坏特征及数值模型单元屈服状态，将其简化为如图14所示的2种裂纹发育模式。

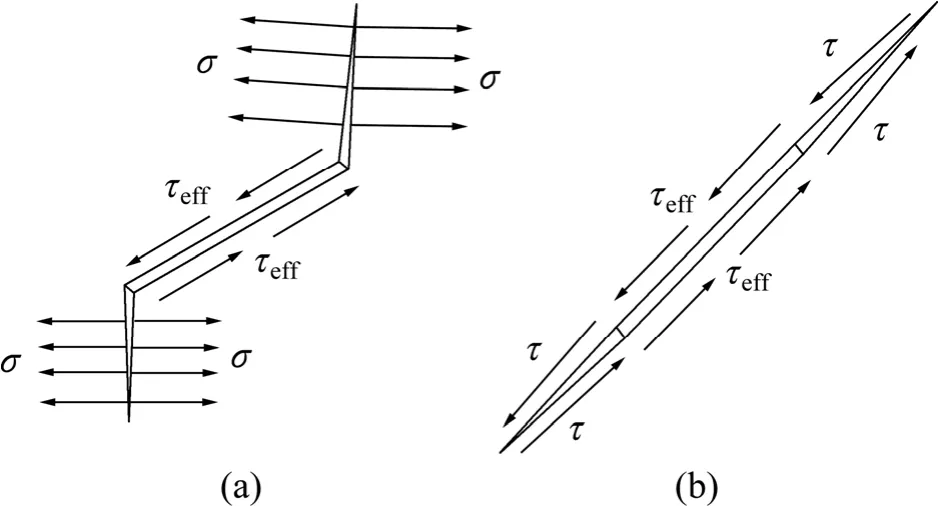
图14 裂隙发育模式简化模型Fig.14 Simplified models of development patterns of fissures:(a) Tensile failure; (b) Shear failure

图 14(a)所示为近置裂隙发生拉伸或拉剪复合破坏时简化模型，裂隙尖端微裂纹开裂由周向正应力驱动，其贯通微裂纹平行或近于平行最大主应力方向，此类破坏模式可以简化为裂隙尖端微裂纹在周向主应力驱动下平行最大主应力方向扩展。

图 14(b)所示为近置裂隙发生剪切破坏时简化模型，虽然裂隙面上的有效剪切力仍是驱动应力，但是其力学行为与图 14(a)所示并不相同，有效剪应力 τeff诱发近置裂隙岩桥发生剪切破坏，且裂纹扩展方向与裂隙走向一致，单轴压缩下表现为压剪破坏模式，实验过程中岩桥区由剪应力诱发次生共面裂纹搭接贯通，其路径平行或近于平行裂隙走向。

1) 破坏模式为图 14(a)所示模型时：根据式(4)，微裂纹尖端Ⅰ型应力强度因子表达式为：

2) 破坏模式为图 14(b)所示时，剪切破坏发生在两条裂隙之间的岩桥区域内，设岩桥长度为 L，此时微裂纹扩展的驱动力除裂隙面上有效剪切力外，还包括岩桥区潜在剪切面上的剪应力，根据摩尔-库伦准则得到岩桥区剪切破坏临界应力表达式：

式中：c为黏聚力；φ为内摩擦角。

据此得到近置裂隙间岩桥发生剪切破坏时的初裂强度表达式：

式(6)与(10)分别给出了近置裂隙破坏时的2种简化裂纹贯通模型初裂强度表达式，实验条件下破坏模式要复杂很多，拉伸与剪切破坏往往同时出现，只是其中某种破坏占主导作用，这主要与裂隙的相对分布特征有关，相关的研究工作已经取得了不少有价值的研究成果和结论，但是对近置裂隙相互作用机制的理论解释仍然不够充分。

4.3 算例分析

为研究2种简化模型的可行性，本研究以本次实验近置多裂隙体为分析对象进行验证。

蒲成志等[1]总结得到本实验预制裂隙材料强度分布规律：25°倾角裂隙体的强度小于45°倾角裂隙体试件的。忽略试件预制过程中的个体差异性，可以认为这类裂隙体试件具有相同的裂隙特征：即裂隙面摩擦因数相等。基于实验结论可以判断：

根据式(12)与式(1)可以得到：

基于数值分析结果，假设α=30°时裂隙体取得强度最小值，此时：

根据简化模型假设：近置裂隙岩桥区发生拉伸或拉剪复合破坏时微裂纹初始起裂方向均为平行最大主应力方向。据此结合式(6)和(7)可以分别得到倾角为25°和 45°时裂隙尖端发育图如图 14(a)所示简化微裂纹的初始强度表达式：

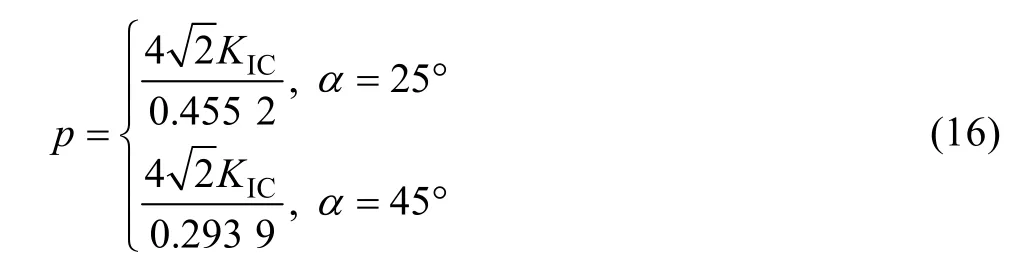
式中：p的单位为MPa；

式(16)表明：本实验中25°倾角裂隙尖端发育平行最大主应力方向微裂纹所需初始起裂强度较 45°倾角裂隙的小，与实验结果相一致。

同理，近置裂隙岩桥区发生剪切破坏时，剪切滑动面与裂隙面平行，此时剪切滑动面穿过的岩桥长度L也为考虑变量。据此结合式(8)、(10)及表 1中材料力学参数可以分别得到 25°和 45°时裂隙尖端发育图(见图14(b))所示简化微裂纹的初始强度表达式：

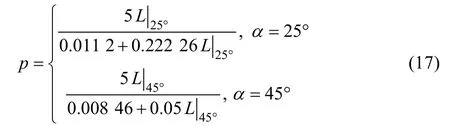
式(17)表明：裂隙尖端发育初始剪切裂纹所需初始强度与对应岩桥长度有关。

根据图14所示简化模型，25°倾角裂隙体近置裂隙尖端发育剪切裂纹贯通时，其贯通路径将图 15所示。

实测试件中岩桥(剪切带)长度为52.43 mm，根据式(17)可以得到 25°倾角近置裂隙发生剪切破坏初始起裂强度为 11.47 MPa；实验中试件发生近置裂纹的拉剪复合破坏强度最大为6.84 MPa；因此在实验状态下，25°倾角裂隙体近置裂隙间岩桥区并没出现剪应力主导的剪切破坏，而是以周向拉应力主导的拉伸或拉剪复合破坏为主。据此得到简化模型与试验结果相符，证明本研究提出的2种简化模型的正确性，并具有可行性。

图15 25°倾角近置裂隙剪切裂纹发育形态Fig.15 Spatial morphologies of shear cracks at tips of ordered fissures with inclination angle of 25°

5 结论

1) 有序分布多裂隙脆性试件中，除裂隙倾角及其几何排布外，预制裂隙在试件中的相对分布位置也影响着裂隙体破坏特征；其影响强度与裂隙面上有效剪切力大小相关：有效剪切力大时显著，反之则不明显。

2) 同一试件中，裂隙特征及其几何排布相同时，裂隙尖端发育微裂纹机率并不相等；在试件中存在一个优势破坏面，它与试件的一条斜对角线重合，该对角线与裂隙走向一致；当裂隙分布在优势破坏面上或优势破坏面两侧附近时，其尖端发育微裂纹的机率大于其他位置，而分布在另一条斜对角线端部的裂隙最稳定。

3) 近置裂隙发生贯通破坏时，根据其破坏特征及数值模型单元屈服状态，将裂隙尖端微裂纹发育形态简化为2种模型，并结合本次试验结果验证了简化模型的可行性。

REFERENCES

[1] 蒲成志, 曹 平, 赵延林, 张向阳, 衣永亮, 刘业科. 单轴压缩下多裂隙类岩石材料强度试验与数值分析[J]. 岩土力学,2010, 31(11): 3661-3666.

PU Cheng-zhi, CAO Ping, ZHAO Yan-lin, ZHANG Xiang-yang,YI Yong-liang, LIU Ye-ke. The numerical analysis and strength experiment of rock-like material with multi-fissures under uniaxial compression[J]. Rock and Soil Mechanics, 2010, 31(11):3661-3666.

[2] 沈珠江. 岩土破损力学与双重介质模型[J]. 水利水运工程学报, 2002, 23(4): 1-6.

SHEN Zhu-jiang. Breakage mechanics and double medium model for geological materials[J]. Hydro Science and Engineering, 2002, 23(4): 1-6.

[3] 沈珠江. 岩土破损力学: 理想脆弹塑性模型[J]. 岩土工程学报, 2003, 25(3): 253-257.

SHEN Zhu-jiang. Breakage mechanics for geological materials:An ideal brittle-elasto-plastic model[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(3): 253-257.

[4] 陈铁林, 沈珠江. 岩土破损力学的系统论基础[J]. 岩土力学,2004, 25(s2): 21-26.

CHEN Tie-lin, SHEN Zhu-jiang. System approach of breakage mechanics for geological materials[J]. Rock and Soil Mechanics,2004, 25(s2): 21-26.

[5] 黎立云, 许凤光, 高 峰, 王 利, 车发星. 岩桥贯通机理的断裂力学分析[J]. 岩石力学与工程学报, 2005, 24(23):4328-4334.

LI Li-yun, XU Feng-guang, GAO Feng, WANG Li, CHE Fa-xing. Fracture mechanics analysis of rock bridge failure mechanism[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(23): 4328-4334.

[6] 黄明利, 唐春安, 梁正召. 岩石裂纹相互作用的应力场分析[J]. 东北大学学报: 自然科学版, 2001, 22(4): 446-449.

HUANG Ming-li, TANG Chun-an, LIANG Zheng-zhao. Stress field analysis of interaction of rock cracks [J]. Journal of Northeastern University: Natural Science, 2001, 22(4): 446-449.

[7] 唐春安, 黄明利, 张国民, 焦明若. 岩石介质中多裂纹扩展相互作用及其贯通机制的数值模拟[J]. 地震, 2001, 21(2): 53-58.

TANG Chun-an, HUANG Ming-li, ZHANG Guo-min, JIAO Ming-ruo. Numerical simulation on propagation, interaction and coalescence of multi-cracks in rocks[J]. Earthquake, 2001, 21(2):53-58.

[8] BOBET A. The initiation of secondary cracks in compression[J].Engineering Fracture Mechanics, 2000, 66: 187-219.

[9] PARK C H, BOBET A. Crack coalescence in specimens with open and closed flaws: A comparison[J]. International Journal of Rock Mechanics & Mining Sciences, 2009, 46: 819-829.

[10] 李银平, 杨春和. 近置多裂纹相互作用的渐近分析方法[J].力学学报, 2005, 37(5): 600-605.

LI Ying-ping, YANG Chun-he. Asymptotic analysis of interaction of closely-spaced cracks[J]. Chinese Journal of Theoretical and Applied Mechanics, 2005, 37(5): 600-605.

[11] 蒲成志. 单轴压缩下类岩体裂隙材料断裂破坏机制的实验研究[D]. 长沙: 中南大学, 2010.

PU Cheng-zhi. Experiment research on the fracture failure mechanism of rock-like material with fissures under uniaxial compression[D]. Changsha: Central South University, 2010.

[12] 赵延林. 裂隙岩体渗流-损伤-断裂耦合理论及应用研究[D].长沙: 中南大学, 2009.

ZHAO Yan-lin. Coupling theory of seepage-damage-fracture in fractured rock masses and its application[D]. Changsha: Central South University, 2009.

[13] 张 平. 裂隙介质静动应力条件下的破坏模式与局部化渐进破损模型研究[D]. 西安: 西安理工大学, 2004.

ZHANG Ping. Research on the failure patterns and localized progressive failure models of the cracked media under static and dynamic stress condition[D]. Xi’an: Xi’an University of Technology, 2004.

[14] HUTCHINSON J W. Crack tip shielding by microcracking in brittle solids[J]. Acta Metall, 1987, 35: 1605-1619.

[15] 陈蕴生, 李 宁, 韩 信, 蒲毅彬, 廖全荣. 非贯通裂隙介质裂隙扩展规律的CT试验研究[J]. 岩石力学与工程学报, 2005,24(15): 2665-2670.

CHEN Yun-sheng, LI Ning, HAN Xin, PU Yi-bin, LIAO Quan-rong. Research on crack developing process in noninterpenetrated crack media by using CT[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(15): 2665-2670.

Failure mechanism and its simplified models of brittle material with ordered multi-fissures under uniaxial compression

CAO Ping, PU Cheng-zhi
(School of Resource and Safety Engineering, Central South University, Changsha 410083, China)

The loading tests were done on the brittle specimens with ordered multi-fissures which were made by pulling out the metallic shims at the early stage in the curing process under a uniaxial loading system with servo control. The numerical models of fissure bodies were established based on the strain-softening mechanism of brittle material with local damage characteristics under uniaxial compression. The failure mechanism and its influencing factors of brittle material with ordered multi-fissures were analyzed by comparing experiment results with numerical calculations. The results show that the failure characteristics of specimens are also influenced by the relative position of fissures besides the fissure inclination angle and its geometrical arrangement, and the influence degree has relationship with the effective shear stress on fissure surface. The larger the effective shear stress is, the more significant the influence is. The experimental results and numerical calculations show that a dominant failure surface exists in the specimen with ordered multi-fissures, which is coincident with the diagonal that has the same strike with fissures. The probability of micro-cracks appearing at the tips of fissures, which distribute in or are close to the dominant failure surface, is larger than the probability of the ones which are far from the dominant failure surface. Combined with the failure characteristics of specimens with ordered multi-fissures and yield situations of grid cells in numerical models, two kinds of simplified models are proposed to describe the spatial morphologies of closely-spaced fissures. Then, combined with this experimental result, the feasibility of simplified models is verified.

brittle material; ordered multi-fissures; failure mechanism; simplified model; dominant failure surface;strain-softening

TU5

A

1004-0609(2011)10-2659-10

国家自然科学基金资助项目(10972238)

2011-05-20；

2011-07-20

曹 平，教授，博士；电话：13973128263；E-mail: pcao_csu@sina.com