线控转向汽车的ADAMS/MATLAB联合仿真
张乔 ,冯樱 ,张光德
(1.武汉科技大学 汽车与交通工程学院,湖北 武汉430081;2.湖北汽车工业学院 汽车工程系,湖北 十堰442002)
目前,汽车转向系统主要处在机械转向阶段,由于传动比设置在某一固定值或小范围内变化,汽车的转向特性随着车速和转向盘转角的变化而变化。 线控转向系统(Steering-by-Wire System)取消了方向盘与转向轮之间的机械连接,使转向车轮完全摆脱机械连接的束缚,可以根据需要自由的设计角传动比,通过电子控制单元对汽车转向进行控制,实时地调节汽车前轮转角和方向盘路感,以获得最佳的驾驶性能,既减轻了驾驶员的负担,又提高了汽车的操纵稳定性[1-3]。本文根据线控转向汽车的特点,基于ADAMS软件建立了线控转向整车多体动力学模型;利用MATLAB软件编写的控制策通过ADAMS/Control接口模块实现了典型行驶工况下的联合仿真,并与机械转向汽车仿真试验结果进行比较,结果表明线控转向汽车具有更好的稳定性。
1 基于ADAMS/CAR整车建模
ADAMS/CAR模块是MDI公司与奥迪Audi、宝马BMW、雷诺Renault和沃尔沃VOLVO等公司合作开发的轿车分析软件包,集成了在汽车设计与开发方面专家的经验[4],主要用于非线性机械多体动力学仿真分析。整车的建模过程:首先在Template Builder模板中创建汽车各个子系统模板,再创建子系统,然后将所建立的子系统生成整车。整车主要包括7个子系统:车身系统、转向系统、动力系统、前后悬架系统、制动系统和轮胎。
1.1 线控转向系统模型
线控转向系统的结构可以分为3部分,第1部分是方向盘系统,包括方向盘、减速机构、转向力矩传感器、转向角传感器和转矩反馈电机等;第2部分是电子控制系统,包括电子控制单元、车速传感器、横摆角速度传感器、加速度传感器等;第3部分是转向执行系统,包括转向电机、减速机构、转向器、角位移传感器等。建模时将机械转向系统中连接转向柱和转向输入轴的中间轴打断,在方向盘处建立减速机构和路感反馈电机,用于反馈力矩的输入;在小齿轮处建立减速机构和转向电机,用于驱动前轮转向,同时为了模拟反馈子系统的刚度,在反馈电机与转向柱间安装了轴套,转向机构中的各种传感器通过定义系统的状态变量来模拟,ECU控制是通过MATLAB编写的控制策略实现的,建立完成的模型如图1所示。
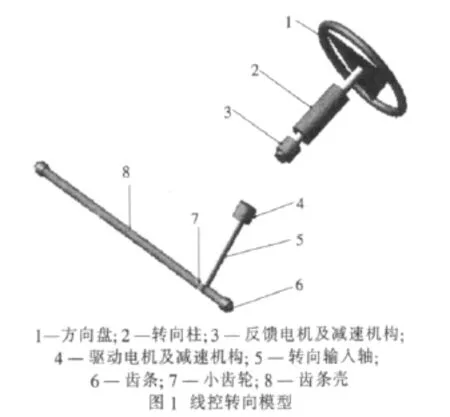
1.2 轮胎及其它系统模型
本文选取魔术轮胎作为仿真轮胎模型,魔术轮胎模型是用三角函数的组合公式拟合轮胎的试验数据,用一套形式相同的公式来完整地表达轮胎纵向力、侧向力、回正力矩、翻转力矩、阻力矩,以及纵向力、侧向力的联合作用工况,魔术公式的一般表达式为[4]

式中:D—峰值因子,表示曲线的最大值;C—曲线形状因子;X—表示轮胎的侧偏角或纵向滑移率;B—刚度因子。
悬架模型采用双横臂独立悬架(这里前后悬架模型均采用双横臂独立悬架),发动机模型采用V6缸发动机,布置形式为发动机后置后驱,制动系模型采用钳盘式制动器,定义一个单作用力矩来模拟制动器的制动力。线控转向整车动力学模型的主要参数:整车质量为1527kg;轴距为2560mm;质心距前轴的距离为1186mm;质心高为365mm;绕z轴转动惯量为6014 kg·m2,整车模型如图2所示。

2 控制策略建立
由于线控转向汽车取消了方向盘与转向轮之间的机械连接,车轮的转向运动是ECU根据当前方向盘转角、汽车的行驶状态及传动比对驱动电机进行控制实现的,因此,传动比对汽车的控制效果起着至关重要的作用。
2.1 传动比设计
借用机械转向传动比的定义,线控转向的传动比定义为方向盘转角与前轮转角的比。汽车横摆角速度ω与前轮转角δf的比,用符号Gf表示,稳态条件下可表示为

汽车横摆角速度ω与方向盘转角δh的比,用符号Gh表示,稳态条件下可表示为

因此,线控转向的传动比i可以表示为

从式(4)可以看出,线控转向的传动比与稳态增益Gf和Gh有关,Gf只与汽车的轮胎、悬架、整车质量等参数有关,而Gh不仅与汽车的轮胎、悬架、整车质量等参数有关外,还与传动比i有关。文献[5]中指出当稳态增益Gh一定时(对应的传动比称之为理想传动比),就可以保证汽车的路径行驶角与方向盘转角一一对应的关系,只要合理地选取Gh,就能在很大程度上减轻驾驶员的负担,提高汽车的操纵稳定性。假定任何已知车速和方向盘转角条件下,Gh恒为常量,根据原联邦德国几个大学的汽车研究所通过对近代小轿车进行试验后统计得出:轿车的稳态横摆角速度增益,即Gh为0.16~0.33 s-1,相应的试验工况为车速 22.35 m·s-1,侧向加 速 度 0.4 g[6], 本 文 选 取 Gh为 0.23 s-1, 利 用ADAMS所建立的线控转向汽车动力学模型分别进行方向盘转角为 10°、20°、40°、60°、80°、100°的角阶跃输入仿真试验,车速从10 km·h-1开始,以10 km·h-1间隔逐渐增加到 140 km·h-1,即同一方向盘转角输入下不同车速的角阶跃仿真,当车速增加到横摆角速度无法收敛时停止,每次仿真完成后,用横摆角速度除以方向盘转角,得到稳态横摆角速度增益Gh,将Gh与0.23进行比较,并根据式(4)计算出理想的传动比。仿真得到的理想传动比与方向盘转角的关系曲线如图3所示。

2.2 线控转向控制器设计
线控转向ECU根据传感器采集的方向盘转角、车速、横摆角速度等汽车信号对驱动电机进行控制,联合仿真通过在转向系统模板和车身系统模板定义ADAMS输出状态变量来模拟各种传感器,定义的输出变量为方向盘转角、车速、横摆角速度和侧向加速度,这些状态变量实时输出汽车状态信号到MATLAB控制器中,控制器根据汽车信号实时计算出驱动电机转角,并通过所定义的ADAMS输入变量输出到线控转向的驱动电机中进行转向控制。
MATALB控制器采用变传动比和横摆角速度综合控制策略对线控转向汽车进行控制,以汽车横摆角速度和质心侧偏角为控制参数,汽车的实际横摆角速度由状态变量输出,质心侧偏角由估计器计算得到。获得了汽车实际的横摆角速度和质心侧偏角后,将实际的横摆角速度和质心侧偏角分别与各自的期望值进行比较,并对二者的偏差进行模糊控制,得到控制器的控制转角输出到驱动电机进行控制。
汽车期望的横摆角速度ωd由线性二自由度汽车模型计算得到,计算公式:

由于实际质心侧偏角难以测量或测量成本昂贵,目前主要采用估计的方法得到,本文采用式(6)计算汽车的质心侧偏角[7]。

式中,ay—汽车的侧向加速度;u—车速;ω—汽车的横摆角速度。实际汽车的质心侧偏角希望越小越好,本文设置期望的质心侧偏角零,即βd=0。
2.3 模糊控制器设计
本文采用二维模糊控制器,即以控制变量的误差E和误差变化率EC为控制器的输入,这类控制器类似于PI控制器,可以使系统具有较好的动态性能和稳态精度,因而获得了广泛的应用。定义横摆角速度误差E的论域为[-8,8],误差变化率EC的论域为[-50,50],输出变量 U 的论域为[-1,1];质心侧偏角误差 E的论域为[-10,10],误差变化率EC的论域为[-50,50],输出变量U的论域为[-1,1],2个模糊控制器的输入、输出模糊集个数均为 7 个,即负大(NB)、负中(NM)、负小(NS)、零(ZE)、正小(PS)、正中(PM)、正大(PB)。 确定了输入输出量的变化范围后,对输入量进行模糊化处理,同时确定输入输出量的隶属度函数,隶属度函数的形状在达到控制要求方面无大的差别,倒是隶属函数的幅宽大小对性能影响较大,所以一般选用三角形、梯形隶属度函数作为模糊子集的隶属度函数,这是因为他们的数学表达式和运算较简单,所占内存空间小,在输入值变化时,比正态分布或钟形分布隶属函数具有更大的灵活性,当存在一个偏差时,能很快反应产生一个相应的调整量输出[8]。这里输入、输出变量的隶属度函数均选为三角形隶属度函数,横摆角速度误差E的隶属度函数如图4所示,其余的隶属度函数从略。

通过对输入、输出变量模糊集的选取,共确定49条控制规则,模糊语句采用“If…,then…”条件句,模糊推理采用Mamdani方法,去模糊的方法为面积重心法,编写的规则如下:
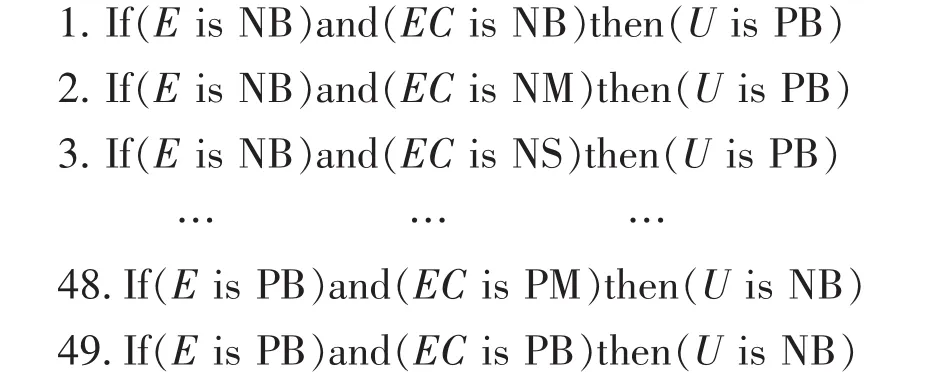
利用上述规则对横摆角速度和质心侧偏角的误差及误差变化率进行模糊控制,实时调节驱动电机的输出转角,控制汽车的转向轮按期望的轨迹行驶。具体规则如表1~2所示。
将上述设计的模糊控制器加入到线控转向控制器中,就完成了整个线控转向控制策略的设计,所搭建的控制策略如图5所示。

表1 横摆角速度模糊规则表
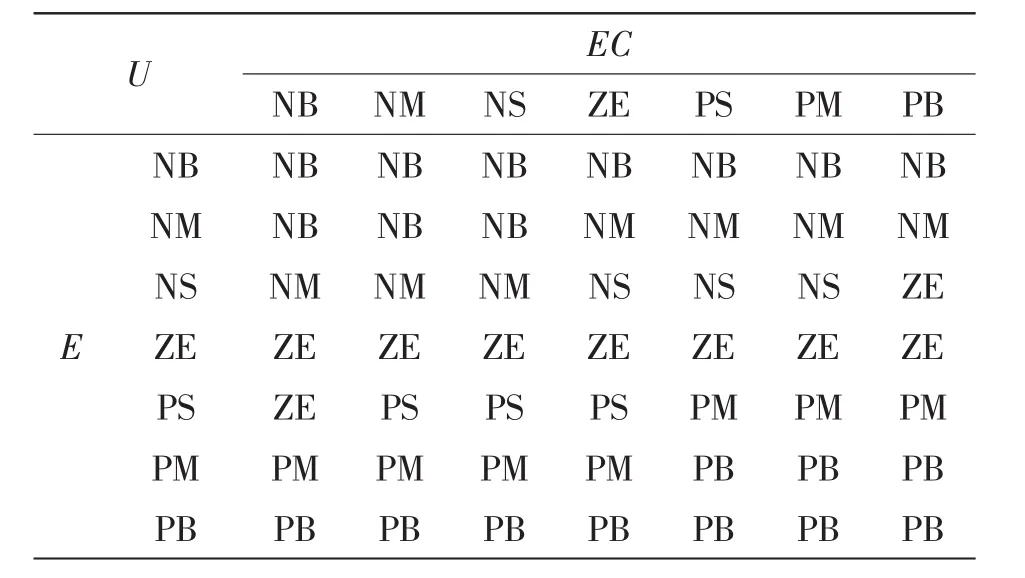
表2 质心侧偏角模糊规则表

3 联合仿真及结果分析
联合仿真选取2种典型试验工况:单移线试验和前轮角阶跃试验。试验条件:初始车速为90 km·h-1,仿真时间为 6s,湿路面路面附着系数 φ为0.5,单移线试验方向盘最大转角为72°,正弦输入开始时间为1s,频率为0.5Hz;角阶跃试验方向盘转角为55°,阶跃开始时间为1s。2项试验分别将线控转向和机械转向汽车的横摆角速度和质心侧偏角的响应曲线进行了比较,仿真结果如图6~7所示。

角阶跃试验,线控转向汽车的横摆角速度和质心侧偏角都更加接近期望值,虽然单移线试验的横摆角速度曲线偏离了期望曲线,但却保证了汽车的稳定性,其操纵性能明显优于机械转向汽车,从而验证了线控转向整车动力学模型的正确性和控制策略的有效性。
4 结论
通过对线控转向汽车进行单移线和前轮角阶跃的ADAMS/MATLAB联合仿真试验研究,得到如下结论:
1)所搭建的变传动比和横摆角速度综合控制策略能控制汽车较好地适应湿路面条件,汽车横摆角速度得到较好跟踪,质心侧偏角得到较好抑制,有效地提高了线控转向汽车的稳定性。
2)利用机械系统多体动力学软件ADAMS建立整车动力学模型,并和控制软件MATLAB搭建的控制策略进行联合仿真,是研究线控转向汽车的有效方法。
[1] 宗长富,郑宏宇,田承伟,徐颖.线控转向稳态增益与动态反馈校正控制算法[J].汽车工程,2007,29(8):686-691.
[2] Yixin Yao.Vehicle Steer-by-Wire System Control [J] .SAE Technical Paper Series,2006-01-1175.
[3] Sanket Amberkar,Farhad Bolourchi,Jon Demerly, Scott Millsap.A Control System Methodology for Steer by Wire System[J].SAE Technical Paper Series,2004(1):1106.
[4] 陈军.MSC.ADAMS技术与工程分析实例[M].北京:中国水利出版社,2008:165.
[5] 左建令.汽车电子转向系统控制方法研究[D].长春:吉林大学,2003.
[6] 余志生.汽车理论[M].北京:机械工业出版社,2007:148.
[7] 高斯.汽车动力学稳定系统仿真及优化[D].武汉:华中科技大学,2006.
[8] 杨胜兵.线控转向系统控制策略研究[D].武汉:武汉理工大学,2008.

