基于ANSYS Workbench及APDL的鼓式制动蹄有限元分析

张建辉，严运兵，马迅

(1.武汉科技大学 汽车与交通工程学院，湖北 武汉430081；2.湖北汽车工业学院 汽车工程系，湖北 十堰442002）

汽车的制动性是汽车安全行驶的重要保障，与制动性能直接相关的是制动器，而制动器的设计关键在于制动蹄［1］。伴随汽车研发周期的不断缩短，如何快速有效的对制动蹄进行校核有着现实意义。ANSYS Workbench能够快速建立有限元分析模型，但是无法实现复杂载荷的加载。ANSYS的参数化设计语言APDL（ANSYS Parametric Design Language）可以很好的实现参数化建模、复杂载荷加载、求解、后处理、二次开发及优化设计等［2］。因此可以在ANSYS Workbench平台下引入APDL语言对某鼓式制动器的制动蹄进行快速有限元分析。

1 制动蹄的力学模型

以某商用车的后轮领从蹄式制动器的制动蹄为研究对象。对制动蹄的分析取2种工况：1）静载荷工况，考察的是蹄鼓刚刚接触时的工况；2）制动鼓转动，模拟车辆运动过程中采取制动的工况。

1.1 静载荷工况

图1为蹄鼓刚刚接触时领蹄的受力简图。制动蹄在促动力F1的作用下绕支撑销张开，与转动的制动鼓接触，文献［3］认为制动蹄受到正弦分布的正压力，根据文献［4］可以计算出蹄鼓之间最大正压力。静载荷工况是制动鼓转动时工况的简化形式，此时并无摩擦力作用。根据力的等效原理，可以计算出正压力合力F2的大小与作用点。

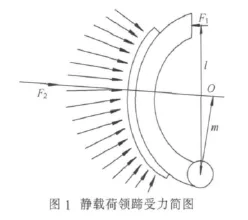
在静载荷工况下，由于没有摩擦力的作用，从蹄的受力情况跟领蹄相同。

综合领蹄和从蹄的力学分析，采用同类普通制动器相关结构的设计尺寸、选择制动气室中的压力为 18kg·cm－2，制动力臂为 110 mm，制动鼓内径为194 mm，摩擦片的包角范围为 31°～149°，制动蹄鼓之间的摩擦系数选0.3。根据文献［5］可以算出领蹄、从蹄的促动力大小。为了更好的模拟真实情况，分析中正压力采用理论分析中得到的正弦分布力，施加在制动蹄与鼓相互接触的表面上。

1.2 制动鼓转动的工况

图2为制动鼓转动时领蹄的受力简图。受力情况与静载荷工况类似，只是此时有存在与正压力相对应的摩擦力。对于等位移制动器，制动时两蹄对鼓的压紧程度相同，因此蹄鼓之间的最大正压力大小相同。由于领蹄摩擦力的增势作用，领蹄的促动力减小。由于从蹄摩擦力的减势作用，从蹄的促动力增大。根据力的等效原理，亦能计算出正压力合力F2、摩擦力合力F3的大小与作用点，将正压力与摩擦力合成得到F的大小及作用点。根据文献［5］可以算出制动鼓转动工况下，领蹄、从蹄的促动力大小。

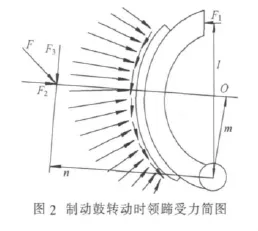
2 有限元模型

分析中用到的制动器与同类型的制动器结构有所不同，它的摩擦衬片并没有安装在制动蹄外表面，而是安装在制动鼓内表面，并且在制动蹄两侧加有侧板。因此对制动蹄应力场分析时不需要再对摩擦衬片建模，正弦分布的正压力及相应摩擦力是直接施加在制动蹄外表面上。同时为了缩减计算时间，在不影响计算准确性的情况下，忽略模型小倒角，去掉比较小的圆孔等［6］。在ANSYS Workbench环境下建立的制动蹄三维实体模型如图3所示。

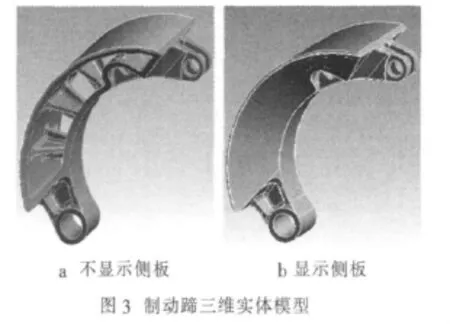
2.1 制动蹄及侧板所用材料

制动蹄材料采用球磨铸铁QT450－10，杨氏模量为 1.68×1011Pa，泊松比为 0.28，密度为 7100kg·m－3。侧板通过多个铆钉与制动蹄进行连接，设置两者之间为绑定接触。侧板的材料为结构钢，杨氏模量为2.0×1011Pa，泊松比为 0.3，密度为 7850 kg·m－3。

2.2 制动蹄有限元模型的建立

采用solid186单元对制动蹄进行结构离散，并用表面效应单元surf 154在制动蹄表面施加正弦分布的压力和与之相应的摩擦力。制动蹄与侧板之间设置为绑定接触，并采用conta174、targe170对接触部分离散。模型的总单元数为69653，节点数为147697。制动蹄有限元模型如图4所示。

3 约束条件与加载过程

制动蹄边界条件合理与否，对有限元分析的计算结果有很大影响。根据实际工作状况，模拟制动蹄与鼓之间完全压紧的状态。

约束制动蹄销孔的径向位移和销孔内端面的轴向位移［7］。在滚轮孔内壁上施加经凸轮传递过来的促动力；在制动蹄外表面上施加经摩擦片传递的正弦分布的压力及相应的摩擦力。

3.1 静载荷工况分析

根据实际工作状况，模拟制动蹄与鼓之间完全压紧的状态。载荷施加经凸轮传递过来的促动力。此时制动蹄与制动鼓刚刚接触并不产生摩擦力，因此在制动蹄外表面只需施加经摩擦片传递的正弦分布的压力。

施加在制动蹄上促动力的大小如表1所示。

表1 静载荷工况时制动蹄上施加的载荷大小

制动蹄外表面上施加正弦分布的压力。

在Ansys Workbench下插入APDL语言加载正弦压力的流程如图5所示。

执行图5用到的APDL语言部分程序如下：提取相关数据的程序：

定义存储正弦分布压力载荷的数组：

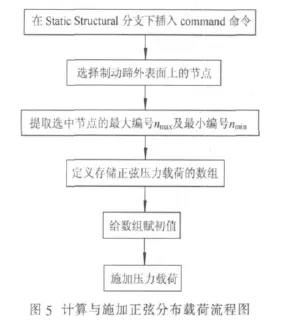
在Ansys Workbench下插入APDL语言加载正弦压力的效果如图6所示。

3.2 制动鼓转动的工况分析

制动鼓转动时，约束与静态工况相同。施加在领从蹄上的促动力大小不同，在制动蹄外表面上施加正弦分布的压力及相应摩擦力。制动蹄所受促动力及表面上的正弦分布压力与相应的摩擦力等数据如表2所示。

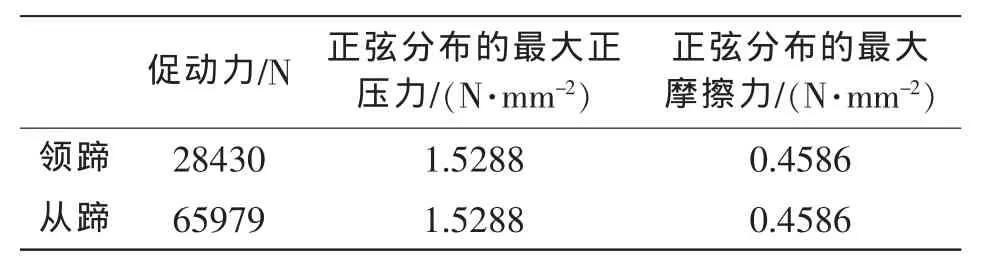
表2 制动鼓转动时制动蹄上施加的载荷大小

ANSYS表面效应单元提供了沿着单元切向施加载荷的方法，因此在制动蹄表面采用surf 154表面效应单元进行了离散。在此基础上，选择蹄外表面节点，定义与切向摩擦力相关数组，即可施加摩擦力。方法及流程与施加正弦分布压力类似。

4 计算结果

4.1 领蹄及从蹄

1）静载荷工况

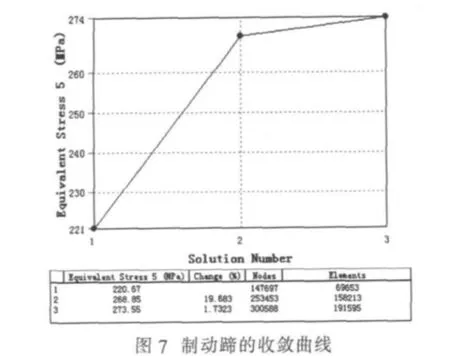
制动蹄的材料为球墨铸铁，在后处理中查看依据第四强度理论计算的Von－Mises应力。由于领、从蹄的有限元模型及边界条件相同，有限元分析结果一样。利用ANSYS Workbench的收敛性功能，在应力最大的地方进行自适应网格划分，经过3次循环后收敛，其收敛曲线如图7所示，最大应力为273.55 MPa，出现在施加促动力附近的结构倒角处，如图8所示。

2）制动鼓转动的工况

领蹄最大应力为251.93 MPa,出现在中间支撑筋的倒角处，如图9a所示。由于领蹄的增势作用，领蹄的促动力减小，同时摩擦力对支撑销孔的力矩增大，使得领蹄在施加促动力附近的结构倒角处的应力减小。从蹄最大应力为384.72 MPa，出现在施加促动力附近的结构倒角处，位置与静载荷工况相同，如图9b所示。由于从蹄的减势作用，需要的促动力增加，从蹄在施加促动力附近的结构倒角处的应力大小明显增大。

4.2 侧板的分析结果

1）静载荷工况

侧板材料为结构钢，在后处理中查看第四强度理论对应的Von－Mises应力，图10中可以看出制动蹄侧板的应力分布情况，最大应力为112.52 MPa，小于结构刚的许用应力极限。在这种工况下，领蹄、从蹄有限元模型及边界条件是一样的，所以应力分布情况相同。

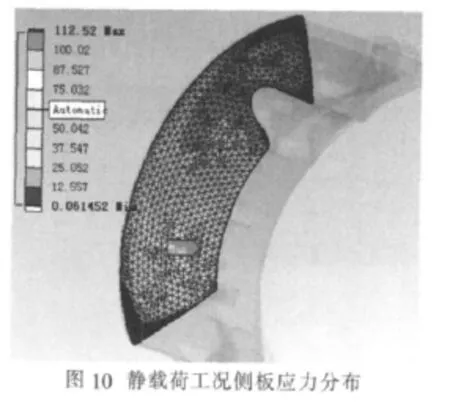
2）制动鼓转动的工况

当制动鼓转动时，领蹄、从蹄侧板处的最大应力分别为131.12 MPa、153.25 MPa，位置如图11所示。由于增加了摩擦力，领、从蹄的应力状态有所改变，最大应力也都有所增大。

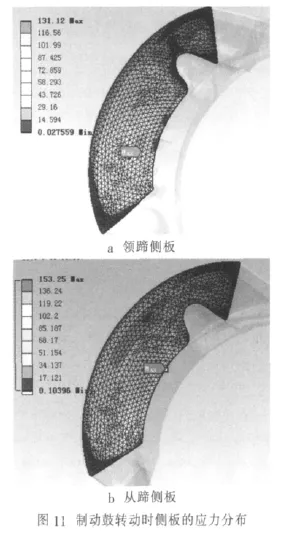
5 结论

在ANSYS Workbench平台下引入APDL语言，可以方便快速的在制动蹄表面施加正弦分布的正压力及相应摩擦力，因此能够较为真实的反应其受力情况。分析了制动蹄的应力情况，得出如下主要结论：

1）从蹄在制动鼓转动工况下，减势作用明显，促动力增大，最大Von－Mises应力的位置不变，但明显增大。虽然满足材料的强度要求，但应力水平偏高。

2）领蹄在制动鼓转动工况时，在摩擦力的减势作用下，促动力减小，同时摩擦力对支撑销孔的力矩增大，因此最大Von－Mises应力的位置发生变化，出现在中间支撑筋的倒角处，应力水平也明显低于从蹄。

3）从侧板的分析结果可以看出，制动鼓转动时，由于领、从蹄的应力状态有所改变，其应力值都比静载荷工况有所增加。

4）基于ANSYS Workbench及 APDL的鼓式制动蹄的有限元分析为进一步优化制动蹄提供了依据。

［1］ 蔡旭东.鼓式制动器热弹性耦合有限元分析［J］.机械强度，2003,25（4）:401－407.

［2］ 秦琴，陶津平，邱峰，蔡国华.基于ANSYS APDL的复杂载荷加载法［J］.计算机辅助工程， 2009,18（2）：92－94.

［3］ 王望予.汽车设计［M］.北京：机械工业出版社，1981：501－506.

［4］ 马迅，秦剑.基于有限元法的制动鼓的耦合分析［J］.机械设计与研究：自然科学版，2005，21（1）：68－71.

［5］ 王宣锋.鼓式制动器动力学性能的研究［D］.哈尔滨：哈尔滨工业大学，2007.

［6］ 马迅，尹长城，陈艳红.基于ANSYS Workbench的鼓式制动器的接触分析 ［J］.湖北汽车工业学院学报，2010，24（3）：1－4.

［7］ 赵波，范平清.鼓式制动蹄的强度刚度分析［J］.上海工程技术大学学报：自然科学版，2007,21（4）：342－355.