二元矩阵有理插值函数的构造

杜伟伟

(安徽教育出版社,安徽合肥 230601)

二元矩阵有理插值函数的构造

杜伟伟

(安徽教育出版社,安徽合肥 230601)

一般构造矩阵值有理函数的方法是利用连分式给出的,其算法的可行性不易预知,且计算量大.本文对于二元矩阵值有理插值的计算,通过引入多个参数,定义一对二元多项式：代数多项式和矩阵多项式,利用两多项式相等的充分必要条件通过求解线性方程组确定参数,并由此给出了矩阵值有理插值公式.该公式简单,具有广阔的应用前景.

二元矩阵值;有理插值;参数;方程组

1 引 言

设x0＜x1＜…＜xn;y0＜y1＜…＜yn,给定矩阵插值节点阵(xi,yj)及相应矩阵Aij=A(xi,yj)∈Rd1×d2(i=0,1,…,n;j=0,1,…,m).

所谓二元矩阵值有理插值,就是寻求矩阵值有理函数

使之满足条件

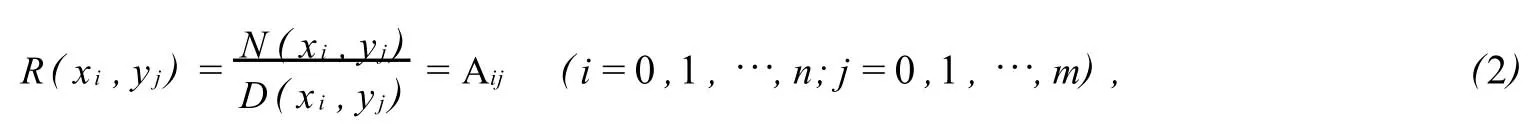
其中N(x,y)是矩阵多项式,D(x,y)是实系数多项式,Aij=A(xi,yj).

文献[1]给出了二元Thiele型矩阵值有理插值的有关结果,也可以利用矩阵的行向量列展开概念,将二元向量值有理插值结果应用到矩阵值有理插值情形,给出二元矩阵值有理插值的算法.上述结果虽然很好,但不便于实际应用.

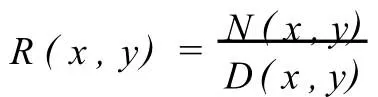
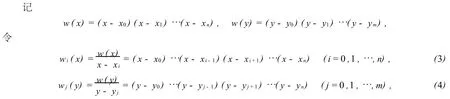
显然wi(x)是n次多项式,wj(y)是m次多项式.记wij(x,y)=wi(x)wj(y).

定义2 对给定的(xi,yj)及相应的矩阵

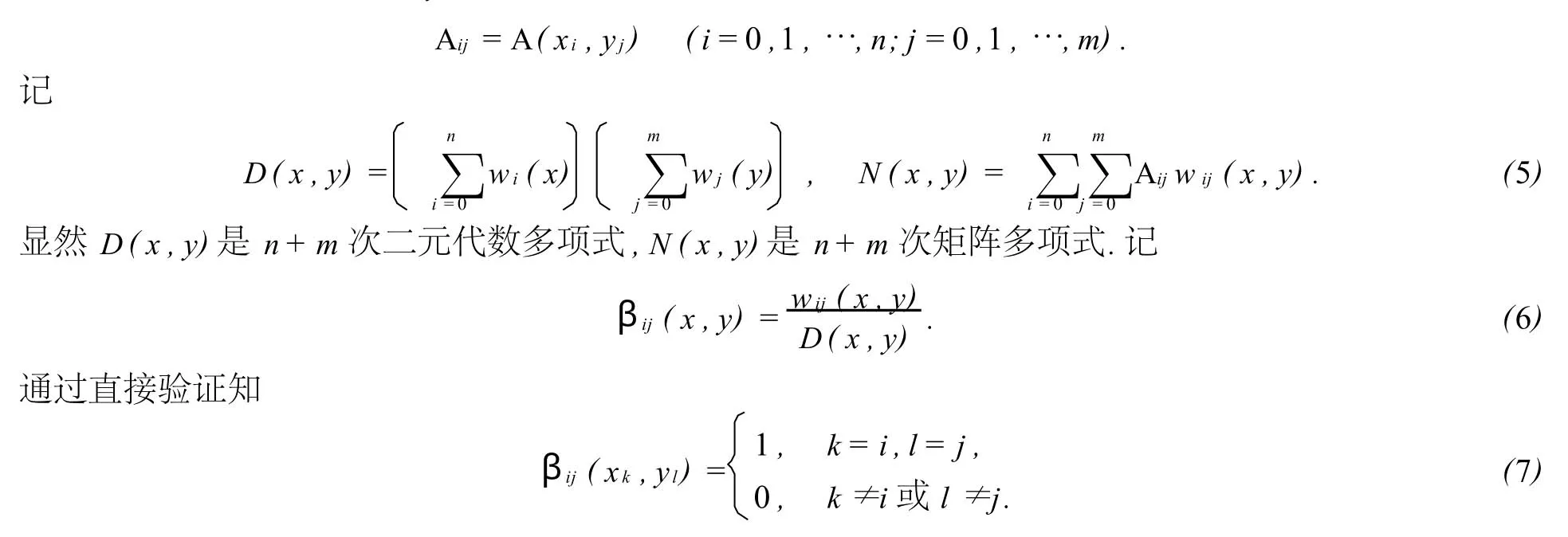
2 二元矩阵值有理插值公式的构造

定理1 对于给定的插值节点(xi,yj)及相应的矩阵

且D(x,y)是n+m次二元代数多项式.

通过观察,容易看出这种构造方式类似于二元Lagrange插值.下面通过例子给出算法的具体步骤.

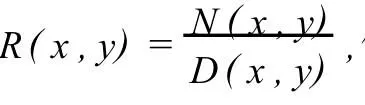
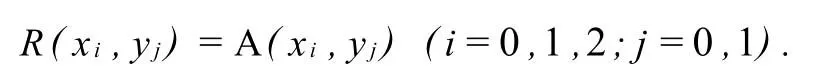
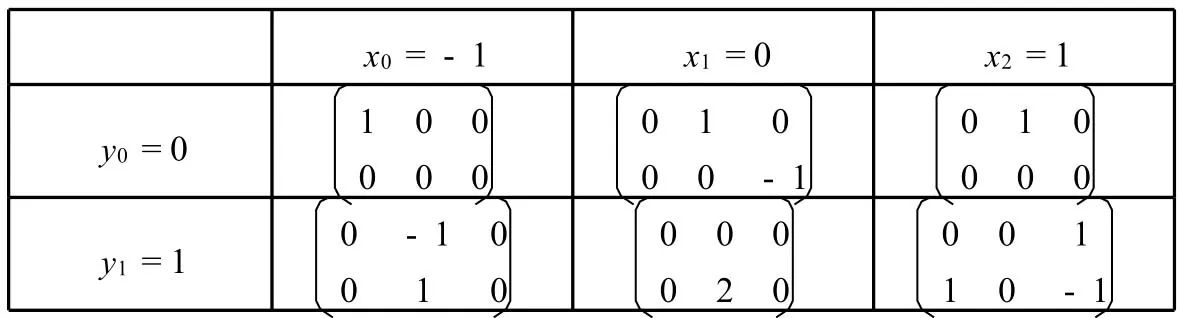
表1

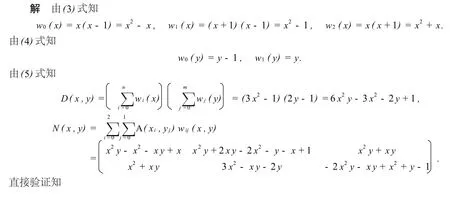
显然,由(8)式构造的二元矩阵值有理插值函数次数较高.为了降低次数,引入参数αij(i=0,1,…,n; j=0,1,…,m),重新定义并仍记D(x,y),N(x,y)和βij(x,y).

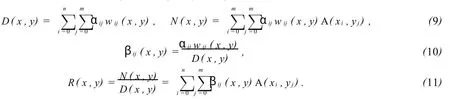
下面给出降低分母多项式D(x,y)次数的方法.由(9)式知D(x,y)最高次项为axnym(a为常数),如果要降低1次,由多项式相等的充分必要条件,可令xnym项系数为零,便得方程(αij为未知量)

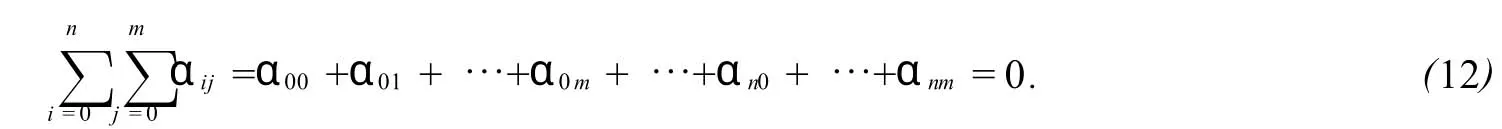
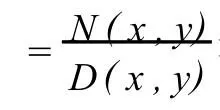
由此便得定理2.

定理2 对于给定的节点(xi,yj)及相应的矩阵值

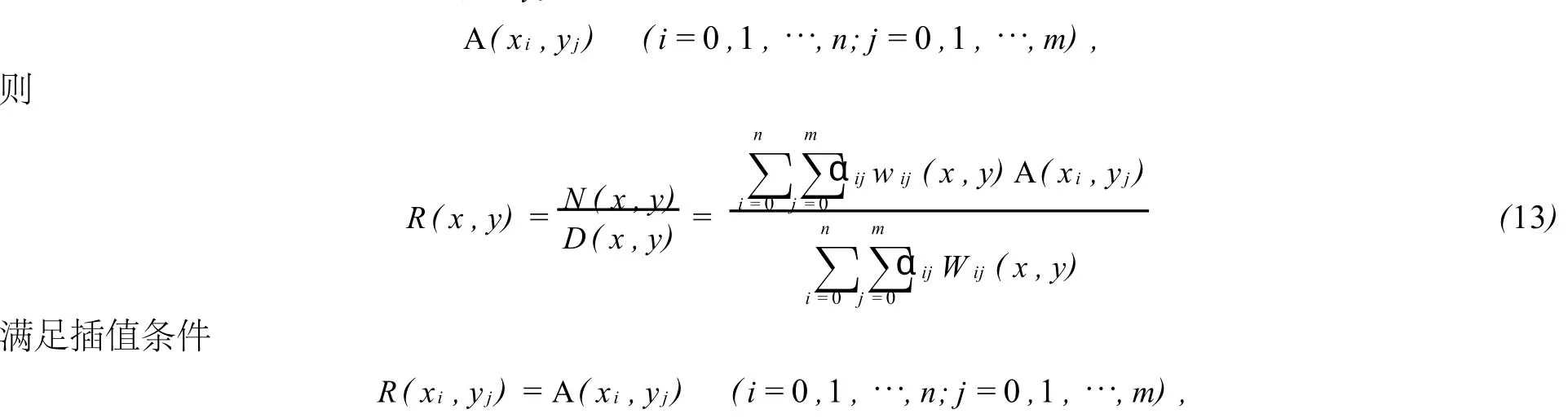
且D(x,y)的类型和次数可根据需要确定.

注意,在构造二元矩阵值有理插值函数R(x,y)时,如果求解过程中存在i0,j0使得αi0j0=0,则R(x,y)在该点(xi0,yj0)处可能不会插值了;如果αij均为非零实数,则该R(x,y)必插值所有节点.

解 在例1中,如果要降低分母次数,希望D(x,y)=x+y-4.由分析知

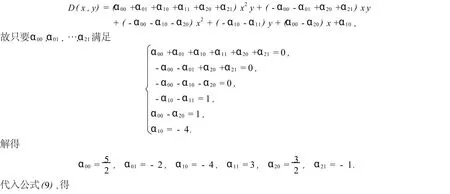
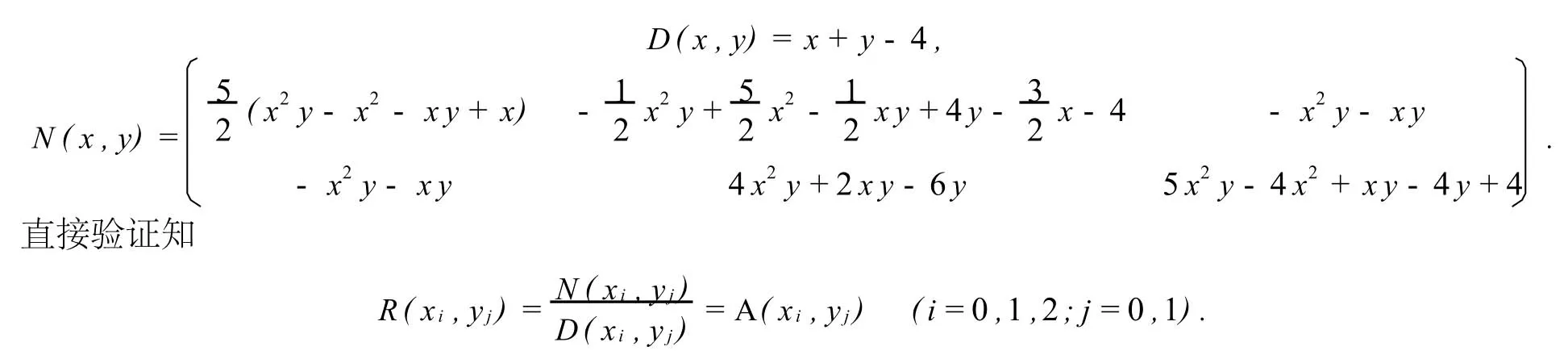
需要指出的是,本文只给出了降低有理函数分母多项式次数的方法.分子是矩阵多项式,如何降低其次数是值得深入研究的.

例3 就例1已知条件,判断分母形如D(x,y)=x+y+1的二元矩阵值有理插值函数是否存在.

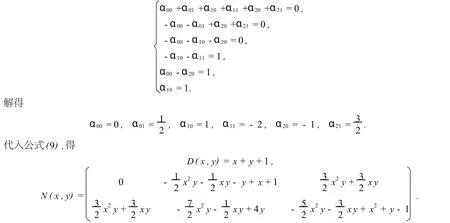
解 与例2类似,考虑方程组但是发现α00=0时,R(x,y)不能插值其所对应的节点(x0,y0),而在其他点满足插值条件.

由定义1易知,由(5),(6)和(8)式定义的矩阵值有理插值函数是[m+n,m+n]型的,由文献[1]中

3 结束语

本文所构造的二元矩阵值有理插值函数类似二元Lagrange插值函数,其构造只考虑节点,不必关心所给的矩阵值.文中构造二元矩阵有理插值方法,具有直观、简单的特点,并且还可根据需要降低分母多项式的次数.以往的二元矩阵有理插值计算大多数是从连分式入手,从而构造出二元Thiele型矩阵有理插值,并且次数较高.本文在计算中都是使用简单的代数知识,便于实际应用.

[1] Zhu G W,Tan J Q.A note on matrix-valuedd rational interpolant[J].Compute Appl Math,1999,110：129-140.

[2] Schneider C,Werne W.Some new aspects of rational interpolation[J].Math Comput,1986,47：285-299.

[3] 顾传青,陈之兵.矩阵有理插值及其误差公式[J].计算数学,1995,(1)：73-77.

[4] 蒋尔雄.线性代数[M].北京：人民教育出版社,1979.

[5] 王仁宏,朱功勤.有理函数逼近及其应用[M].北京：科学出版社,2004.

Method of Constructing Bivariate Matrix-valued Rational Interpolation Functions

DU Wei-wei
(Anhui Education Press,Hefei,Anhui 230601,China)

The well-known algorithms of constructing matrix-valued rational interpolations use continued fractions. Their applicability is not easily forecast and they need a large amount of calculation.In this paper,for calculation of bivariate matrix-valued rational interpolations,multi-parameters are introduced and a group of polynomials with two elements,that is an algebraic polynomial and matrix-valued polynomials,are defined.By using the necessary and sufficient conditions for polynomials identity,linear equations are solved to determine the parameters and the formula of the matrix-valued rational interpolation is given.The formula is simple,so that it has abright application future.

bivariate matrix-valued rational interpolation;parameter;system of equations

O241.3

A

1672-1454(2011)03-0110-05

2008-05-15