线性互补问题测试算例的一个构造方法

杨春艳 (银川大学数学系,宁夏 银川 750105)

雍龙泉 (陕西理工学院数学系,陕西 汉中 723001)

线性互补问题测试算例的一个构造方法

杨春艳 (银川大学数学系,宁夏 银川 750105)

雍龙泉 (陕西理工学院数学系,陕西 汉中 723001)

建立了线性互补问题测试函数的一个构造方法。给出了一般线性互补问题、单调线性互补问题以及反对称矩阵线性互补问题测试算例的构造方法。结果表明，建立的构造方法是有效的。这些结果对线性互补问题的研究具有重要的意义，进而可以利用该方法来构造一系列的线性互补做测试算例，这在很大程度上丰富了线性互补问题的数值试验。

线性互补问题; 测试算例; 单调线性互补; 混合整数线性规划

线性互补问题就是求一个向量x∈Rn，使得：

x≥0Mx+q≥0xT(Mx+q)=0

线性互补问题简记为LCP(q,M)。求解线性互补问题的算法有很多，经典的有Lemke算法。近年来出现的一些具有多项式复杂性的算法，诸如投影法、内点法、非光滑牛顿法、光滑牛顿法等已成为目前研究的热点[1-5]。文献[6]中把线性互补问题转化为一个混合整数线性规划，通过求解混合整数线性规划得到原问题的最优解，该方法更实用，且更容易上机操作，因此也可以作为求解线性互补问题的一个实用方法。

下面，笔者就线性互补问题测试算例的一个构造方法做了研究，给出了一般线性互补问题、单调线性互补问题以及反对称矩阵线性互补问题测试算例的构造方法。

1 一般线性互补问题

随机产生矩阵M∈Rn×n,随机生成非负向量x∈Rn×1,令q=-Mx,因此就得到矩阵M和向量q,由于x≥0,Mx+q=0，故xT(Mx+q)=0,因此相应的线性互补问题LCP(q,M)的解就是x。

算例1随机生成5阶方阵M，随机生成非负向量x∈R5×1；从而得到M和q如下:

根据构造过程可知该问题的一个解是x=(9.7975,2.7145,2.5233,8.7574,7.3731)T，接下来验证其正确性。现将线性互补问题转换成相伴的混合整数线性规划[6]：

其中e=(1,1,…,1)T∈R5,y∈R5,z∈{0,1}5,称(MILP)为LCP(q,M)问题的伴随混合整数线性规划[6-7]，求解(MILP)问题[6]得到a*=0.102067,y*=(1,0.277071,0.257538,0.893844,0.752553)T，由于a*gt;0,故根据文献[6]可知x*=y*/a*=(9.79748,2.7146,2.52322,8.75742,7.37313)T就是原线性互补问题的一个解，由此可见,2个结果是一致的，这说明笔者构造的线性互补问题算例是正确的。

2 对称半正定矩阵线性互补问题

随机产生矩阵A∈Rn×n令M=ATA+kI(其中I是单位矩阵,k≥0)；随机生成非负向量x∈Rn×1,令q=-Mx，因此就得到半正定矩阵M和向量q,同理可知,相应的线性互补问题LCP(q,M)的解就是x。

算例2随机生成5阶方阵A，随机生成非负向量x∈R5×1；进而得到M和q如下:

根据构造过程可知该问题的一个解是x=(8.7437,0.1501,7.6795,9.7084,9.9008)T，接下来验证其正确性。现将线性互补问题转换成相应的混合整数线性规划(MILP)问题，求解(MILP)问题得到a*=0.06513，y*=(0.569522,0.009833,0.5,0.632387,0.644824)T，因为a*gt;0，从而x*=y*/a*=(8.744,0.151,7.677,9.71,9.901)T就是原线性互补问题的一个解，由此可见,2个结果是一致的，这说明笔者构造的线性互补问题算例是有效的。

对称半正定矩阵线性互补问题通常被称为单调线性互补问题，因此调用单调线性互补问题的势下降内点算法[8-9]，得到x*=(8.7444,0.1510,7.6769,9.7096,9.9005)T，可见,2个结果是一致的，这就充分说明笔者构造的线性互补问题算例是正确的。

鉴于M类型的多样性，可以构造更多类型的线性互补问题，比如随机产生矩阵A∈Rn×n，令M=A±AT,这样就可以构造矩阵M为(反)对称的线性互补问题。

3 反对称矩阵线性互补问题

随机产生矩阵A∈Rn×n,令M=A-AT,随机生成非负向量x∈Rn×1,令q=-Mx，因此就得到反对称矩阵M和向量q,由于x≥0,Mx+q=0，故xT(Mx+q)=0,因此相应的线性互补问题LCP(q,M)的解就是x。

算例3随机生成2阶方阵A，随机生成非负向量x∈R2×1，进而得到M和q如下:

根据构造过程可知该问题的一个解是x=(6.4491,8.1797)T。接下来验证其正确性。现将线性互补问题转换成相应的混合整数线性规划(MILP)问题，求解(MILP)问题得到a*=0.122254,y*=(0.788425,1)T,由于a*gt;0,所以根据文献[6]知x*=y*/a*=(6.449073,8.179691)T就是原问题的一个解。由此可见,2个结果基本上一致的。

4 无解线性互补问题

算例4

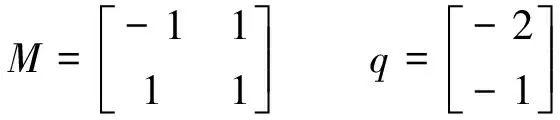
由文献[10]可知该LCP(q,M)问题可行域非空，但是无解。 现将线性互补问题转换成相应的混合整数线性规划(MILP)问题，求解(MILP)问题得到a*=0,y*=(0,0)T,由于a*=0,所以原LCP(q,M)问题无解。

[1]Cottle R W, Pang J S, Stone R E.The Linear Complementarity Problems[M]. Academic Press, 1992.

[2]韩继业, 修乃华, 戚厚铎. 非线性互补理论与算法[M]. 上海:上海科学技术出版社, 2006.

[3]Kojima M, Megiddo N, Yoshise A. A unified approach to interior point algorithms for linear complementary problem[A]. Lecture Notes in computer science[C]. Berlin: Springer-Verlag,1991:538.

[4] Stephen J. Wright. An infeasible-interior-point algorithm for linear complementarity problems[J]. Mathematical Programming, 1994,64:29-51.

[5]何尚录. 求解互补问题的不可行内点法及其计算复杂性[J]. 中国科学A辑, 2000,30(11):983-989.

[6]雍龙泉, 邓方安, 赵景服. 线性互补问题的一种混合整数规划解法[J]. 陕西理工学院学报, 2007,23(4):80-82.

[7]黄红选, 梁治安. 全局优化引论[M]. 北京:清华大学出版社, 2003.

[8] YOANG Long-quan.Potential-reduction interior point algorithm for monotone linear complementarity problem[A]. Proceedings of First International Conference of Modelling and Simulation[C]. UK: World Academic Press, 2008:437-441.

[9]申培萍. 全局优化引论[M]. 北京:科学出版社, 2006.

[10] Kostreva M M, Yang X Q. Unified approaches for solvable and unsolvable linear complementarity problems [J]. European Journal of Operational Research,2004,158: 409-417.

[编辑] 洪云飞

10.3969/j.issn.1673-1409.2011.07.003

O224

A

1673-1409(2011)07-0008-02

2011-05-10

陕西省教育厅自然科学研究项目(09JK381)。

杨春艳，女，助教，现主要从事最优化理论与算法方面的教学与研究工作。