基于周期线的模糊二值形态开路径算法

申雪利,张成斌 (中南民族大学数学与统计学学院，湖北 武汉 430074)

基于周期线的模糊二值形态开路径算法

申雪利,张成斌 (中南民族大学数学与统计学学院，湖北 武汉 430074)

数学形态学作为一门新的自动搜索图形中2点之间的最短路径技术引起了广泛的关注。传统形态学路径算法由于结构元方向的不变性,并不能获取图形中2点之间的最短路径。针对路径的方向变化特征,提出了利用不同方向的周期线结构元的模糊二值形态开路径算法,该算法不仅可获取图形中2点间的最短路径,省略了Lin算法中的距离变换复杂过程,而且该算法简单、易操作。

周期线；模糊二值形态学；开运算；路径

图1 文献[3]算法得到的s点到e点的最短路径 图2 改变结构元方向得到的s点到e点的最短路径

数学形态学采用以结构元与图像的结构匹配程度来获取图像的结构信息,在图像处理和分析中,得到了很好的结果。近年来,数学形态学[1-2]作为一种新的路径搜索技术引起了很多学者的关注,在文献[3]中Lin提出了采用形态学变换来获取图形中2点间的路径[4]算法,而该算法根据传统的数学形态学变换,获取的路径并不是最短的,如图1所示。在C处,如果改变结构元的方向,便可通过,获取s点到e点更短的2点路径，如图2所示。针对文献[3]中的形态学路径最短问题,根据路径的方向变化特征以及周期线结构元的定义,笔者利用不同方向的连通周期线结构元的形态开运算结果取并集,获取图形中的2点间的最短路径。

1 基本概念

1.1数学形态学的基本算子

1)腐蚀与膨胀算子 结构元S对图像集合A进行腐蚀记为AΘS:

结构元S对图像集合A进行膨胀记为A⊕S:

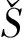
2)开算子 结构元S对图像集合A作开运算记为A∘S或γS(A),即:

A∘S=γS(A)=(AΘS)⊕S

1.2模糊二值开运算

图3 不同的周期线实例

1.3周期线

周期线[5]pm,v的定义如下:

式中，m为周期线上的像素点的数目；v表示常数矢量,矢量v=(a,b),其中a∈Z,b∈Z；周期T=max(|a|,|b|),如图3所示,显示不同的周期线结构元,其中黑色为周期线的原点。

2 算法步骤

基于周期线结构元的模糊二值形态学开运算最短路径算法步骤如下:

Step1 把地图M中障碍物的灰度值设定为1,空白(可通行)区域的灰度值为0,把含有障碍物的地图转化为二值图像A。

Step3HN={x|x∈{γpNm(A)∩γpNk(A),m,k*≤M且m≠k}}

式中，pNm、pNk表示不同方向的N个像素的连通周期线结构元。

Step4 用2个像素的周期线对A1进行模糊二值形态学开运算,得到：

式中，p2m、p2k分别表示为垂直和水平方向的连通周期线。

Step5H=HN∪H2, 在H中搜索始点s点到终点e点的像素数总和最小的连通折线段l便是2点之间的最短路径,否则s点到终点e点之间不存在路径;算法结束。

3 算法试验

利用上述的算法对图4(a)中的二值图像A搜索始点s点到终点e点的路径, 从图4的结果(d)中可获得(a)中s点到e点的可通行区域H,并在可通行区域中,从起点到终点的像素数最少的连通路径便是该算法得到的最短路径。

图4 基于周期线的模糊二值形态开路径算法实现

采用上述的基于周期线的模糊二值形态开路径算法与Lin算法,分别对图5(a)、(b)和(c)中不同的s点到e点的路径进行搜索。由图5(d)、(e)和(f)分别与图5(g)、(h)和(i)进行比较,可得出采用旋转结构元的形态开运算获取的路径较短,而且基于周期线的模糊形态开运算的算法简单,只要采用结构元的不同方向对图进行开运算,并对不同方向结构元的形态开运算结果取并集以及增加2个像素的周期线进行模糊开运算取并集结果,得到了1条连通的实用路径，省去了采用Lin算法中的距离变换的复杂过程。

图5 地图M的2点路径搜索

[1]Serra J. Image Analysis and Mathematical Morphology[M]. New York：Academic Press, 1982:30-50.

[2] Serra J. Image Analysis and Mathematical Morphology: Theoretical Advances [M]. New York：Academic Press, 1988:15-45.

[3] Lin P L,Chang S. A shortest path algorithm for a nonrotating object among obstacles of arbitrary shapes[J],IEEE Trans Systems, Man and Cybernetics, 1993,23(8):825-833.

[4] 宣士斌.基于分流算法的最短路径求解算法[J].计算机工程与应用, 2004 (20):74-76.

[5] Jones R, Soille P.Periodic lines and their application to granulometries[A]. Maragos P, Schafer W, Butt M.Mathematical Morphology and its Application to Image and Signal Processing[C]. Kluwer Academic Publishers,1996:264-272

[编辑] 洪云飞

10.3969/j.issn.1673-1409.2011.07.026

TP391.41

A

1673-1409(2011)07-0073-03

2011-05-27

申雪利，女，硕士生，现主要从事数学应用方法与图像处理方面的研究工作。