Lorenz系统在内分岔参数空间中的新现象探讨

裴启明，蒋 龙 (长江大学物理科学与技术学院，湖北 荆州 434023)

Lorenz系统在内分岔参数空间中的新现象探讨

裴启明，蒋 龙 (长江大学物理科学与技术学院，湖北 荆州 434023)

通过对Lorenz系统的线性稳定性分析，取不动点的2个分量和Lorenz系统的诺雷系数作为参数，构建一个新的参数空间——内分岔参数空间。在该空间下对Lorenz系统进行数值计算，发现了一些新现象，如不动点与周期轨道或混沌吸引子的共存；周期轨道与局部混沌或通向混沌的倍周期分岔序列的共存等。

Lorenz方程；分岔图；共存

19世纪60年代，B.Saltzman和E.N.Lorenz最先在2个无限大平板的热对流模型中导出了Lorenz方程[1]。作为动力学系统中第1个出现奇怪吸引子的例子，Lorenz方程得到广泛而彻底的研究。在常微分方程系统中，不动点的性质对系统的全局行为影响很大。为了找到新现象，把不动点的一些分量作为内参量，并和原来的有关参数一起构成相应的参数空间。在该空间中，可以通过不动点的变化对庞加莱映象所表现的系统的动力学行为进行研究。根据这个思想，笔者构建了一个新参数空间——内分岔参数空间，并在该空间下对Lorenz系统进行数值计算。

1 不动点平面及线性稳定性分析

Lorenz方程为：

(1)

式中，变量x、y、z构成三维相空间；r、σ、b分别为诺雷系数、普朗克常量和几何比率。

设系统(1)的不动点为(x*，y*，z*)，当z*≠0时，有x*=y*，z*=r-1，b=x*2/z*。选择x*、z*充当内分岔参数，保留原参数σ， 建立一个新的参数空间(x*，z*，σ)，称为内分岔参数空间。在该新空间中，Lorenz方程的新形式为：

(2)

将x*-z*平面称为不动点平面。

方程(2)在不动点(x*，y*，z*)的Jacobi矩阵为：

它的3个不等本征值λ1、λ2、λ3是特征方程λ3+a1λ2+a2λ+a3=0的解，其中：

(3)

由Von-Neman理论[2]可知，若所有的特征值λ均满足Re(λ)lt;0，则不动点(x*，y*，z*)是渐近稳定的。又由Routh-Hurwitz判据[2]，通过计算可得a1gt;0，a1a2gt;a3,a3gt;0，即定义了轨道空间中稳定区域的边界线。若取σ=10，由式(3)可知，只要x*≠0均有a3gt;0。因此，只需讨论不等式的前2种情形。

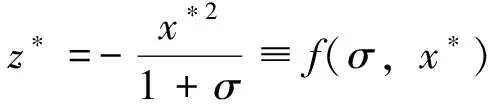
图1 不动点(x*，y*，z*)的渐近稳定区域边界

在此情况下，相空间体积的变化率为：

可见，只要a1gt;0，Λlt;0恒成立，系统是耗散的，此时系统为一个奇怪吸引子。当参数(x*，z*)在该曲线以下时，Λgt;0，系统是发散的，不予以考虑。

此外，几何因子b必须满足b=x*2/z*gt;0，而且b(-x*,z*)=b(x*,z*)。所以，讨论中只要取x*gt;0、z*gt;0。

在不动点平面上，曲线z*=g(σ,x*)位于横轴的上方。在该曲线的下方，参数(x*，z*)满足a1a2gt;a3，不动点是渐近稳定的；反之，不动点是不稳定的。只有当不动点不稳定时，系统才可能出现混沌现象。

综上所述，仅需在不动点平面的第一象限内，在曲线z*=g(σ，x*)及以上部分选取参数(x*,z*)来对系统(2)的动力学行为进行研究。

2庞加莱截面

通过庞加莱截面可以直接将微分方程定义的连续动力系统简化为二维离散动力系统[5]。在对Lorenz系统的研究中，通常以z=r-1作为庞加莱截面。该截面包含系统的2个非平庸不动点：

而且所有有趣的轨道都与它相交[6]。类似地，在内分岔参数空间中，也取z=r-1=z*为庞加莱截面。

3 分岔图及现象

借助庞加莱截面上的分岔图，可以对系统的动力学行为进行探讨。图2为x*=0.5n(n=1,2,…,6)时，z*-x坐标系下的分岔图，其中离散点为分岔序列，2条实线段分别为稳定不动点S+和S-。通过这些分岔图，找到了以下新现象。

3.1几种特殊的共存

1)不动点与周期轨道(用nP表示，n为自然数)的共存 观察图2，当x*=0.5、1.0时不仅有不动点与1P的共存，也有不动点与2P的共存。尤其是x*=1.0时，出现不动点与2P共存的范围更大。不动点与2P的共存在x*=1.5、2.0时也很明显。x*=2.0、2.5时，出现不动点与4P的共存。x*=3.0时，还存在不动点与多种高周期轨道的共存。图3是图2(f)的局部放大图。图3(a)中，当13.8966≤z*≤13.9181时不动点与6P共存；14.0121≤z*≤14.0250时不动点与3P的共存。图3(b)中，当14.4188≤z*≤14.4236时不动点与10P共存；14.4796≤z*≤14.4823时不动点与5P共存。

2)周期轨道与局部混沌的共存 当x*=2.0时，取不同的初值进行数值计算得到分岔图4。其中，实线给出对称的2P轨道中的1支；离散点给出由倍周期分岔而产生的局部混沌。可见，两者在25.0≤z*≤25.4范围内共存。

图2 z*-x坐标系下的分岔图

图3 图2(f)的局部放大图

图4 x*=2.0时，对称的2P轨道(实线)与局部混沌(离散点)共存

3)周期轨道与通向混沌的倍周期分岔序列的共存 当x*=0.5，20.84≤z*≤21.76时，取2个不同的初值，得到分岔图5，其中实线给出对称的2P轨道，离散点给出倍周期分岔序列。由虚线框部分的放大图可知，此时的倍周期序列是由1P轨道经历数次分岔后得到的。对称的2P轨道从z*=21.72开始与该序列中的2P共存，随后与4P共存…，一直持续到z*=21.58时与混沌共存。这是2P轨道与1·2n(n=1,2,3,…)倍周期分岔序列的共存。另一种情形是当x*=3.0，z*值较大时，2P轨道与4·2n(n=0,1,2,…)倍周期序列的共存。图6为x*=3.0,55.3≤z*≤57.0的周期窗口，该图也是取2个不同初值得到的。其中，实线给出对称的2P轨道；离散点给出倍周期分岔序列。若将图中55.3≤z*≤56.3范围的4部分(a)、(b)、(c)、(d)在X轴上放大,发现4部分的结构非常相似，均由1P轨道经倍周期分岔后导致了混沌。所以，对称的2P轨道先与4P共存，之后与8P共存… ，最终与混沌共存。

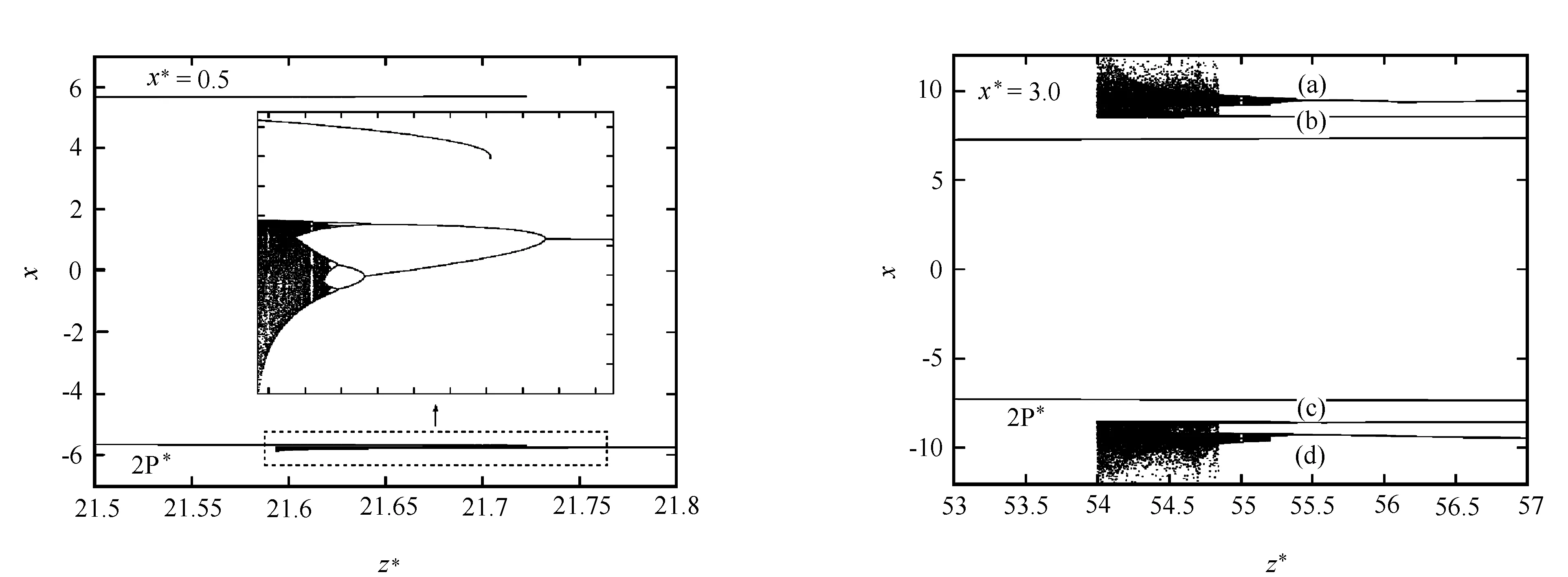
图5 x*=0.5时，对称的2P轨道(实线)与1·2n(n=1,2,3,…)倍周期序列(离散点)共存 图6 x*=3.0时，对称的2P轨道(实线)与4·2n (n=0,1,2,…)倍周期序列(离散点)共存

3.2x*很小时，1P与2P频繁地交替出现

图2(a)中除了在局部极小范围内出现倍周期分岔序列外，在其他区域中1P与2P总是反复交替。图2(b)中， 1P与2P交替得较慢，周期窗口持续得更长。当x*=1.5、2.0时现象更明显。

3.3在z*-x平面存在大量1·2n(n=0,1,2,…)倍周期分岔序列

这些倍周期分岔序列总会导致相空间中较小区域中出现局部混沌吸引子。

4 结 语

在原参数空间中，文献[2-3]认为Lorenz系统在rgt;rh=24.74，3个不动点都不稳定时才出现混沌吸引子，而在内分岔参数空间下，2个非平庸不动点稳定时也能与混沌或各种周期轨道共存。这些特殊现象的发现补充并完善了前人对Lorenz系统的研究，为今后的工作开辟了一条新的研究思路。

[1]Saltzman B. Finite amplitude convection as an initial value problem[J]. J Atoms Sci, 1962，19：329-335.

[2]刘秉正，彭建华.非线性动力学[M].北京：高等教育出版社，2005.

[3]王光瑞，陈光旨.非线性常微分方程的混沌运动[M].广西：广西科学技术出版社，1996.

[4]Hao B L, Liu J X, Zheng W M.Symbolic Dynamics Analysis of the Lorenz Equations[J].Phys Rev E，1998，57：5378-5415.

[编辑] 洪云飞

10.3969/j.issn.1673-1409.2011.07.001

O414.2

A

1673-1409(2011)07-0001-04

2011-04-29

湖北省教育厅重点项目(D20101303)。

裴启明，女，硕士，讲师，现主要从事非线性科学方面的教学与研究工作。