轮滑双蹬技术外刃蹬地动作的加速度情况分析
刘 锋 关汝华
(1.吉林大学 体育学院,吉林 长春 130012;2.吉林大学 数学院,吉林 长春 130012)
轮滑双蹬技术外刃蹬地动作的加速度情况分析
刘 锋1关汝华2
(1.吉林大学 体育学院,吉林 长春 130012;2.吉林大学 数学院,吉林 长春 130012)
探究轮滑运动双蹬技术的外刃蹬地动作是否在前进方向产生了加速度,运用数理演绎方法进行分析。结果:外刃蹬地动作在水平方向上只能产生一个不大的侧向力,当右脚外刃蹬地动作的滑行轨迹处于以运动员总运动方向为y轴的直角坐标系的第Ⅱ象限、或左脚外刃蹬地动作的滑行轨迹处于同一直角坐标系第Ⅰ象限时这个侧向力指向运动员总运动方向的侧后方,产生的加速度与总运动方向呈负值。结论:双蹬技术外刃蹬地动作在水平方向上只能产生一个不大的与总运动方向相反的加速度。
双蹬技术;支撑腿;外刃蹬地;倾斜;速度;加速度;方向
轮滑运动的双蹬技术自出现以来在轮滑运动教练员、运动员中备受推崇,在专业体育期刊和书籍中也有大量运用运动力学分析、评论的文章,一致认为双蹬技术“将传统技术中减速的自由滑进阶段改变为一次利用轮外沿的蹬地,一个单步中增加了一次积极的加速阶段。”[1-4]但我们从人体内力必须作用在外界支撑点上才能起作用的基本原理出发,根据轮滑运动蹬地方向与支撑腿滑行方向相垂直的特点,运用最基本的运动力学知识分析双蹬技术外刃蹬地时支撑腿与地面相互作用力的关系,认为外刃蹬地动作是否在前进方向产生了加速度还值得商榷。
1 轮滑运动正确的蹬地方向与支撑腿滑行方向相垂直
轮滑运动最基本的技术是支撑腿向侧蹬地,正确的动作是蹬地方向与支撑腿滑行方向相垂直,这是由轮滑鞋的几何形状特点不便向后蹬地和向前滑行速度大于支撑腿蹬伸速度决定的[1]。运动力学原理是由支撑腿蹬地的支撑反作用力使身体重心产生向侧移动的加速度后在某一时刻的速度与惯性速度合成一个新的速度,并把身体重心推到新的支撑腿上,沿着新的速度方向前进(见图1)。传统的直道滑行是这样,弯道交叉步滑行是这样,双蹬技术也不能违背这个基本原理。根据运动的合成与分解的平行四边形定则:
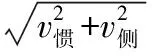
(1)
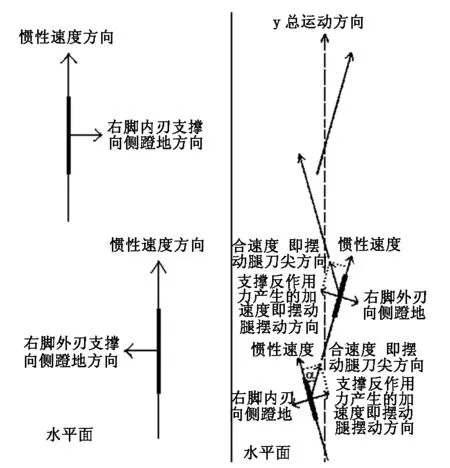
图1 轮滑直道前滑运动力学基本原理图
2 外刃蹬地动作的支撑反作用力符合曲线运动的向心力的特征
双蹬技术的支撑腿向外倾斜向侧蹬地动作(简称外刃蹬地)的支撑反作用力方向与支撑腿的惯性滑行方向相垂直,这个侧向力符合曲线运动的向心力的特征,运动员在切线方向上不受力,没有加速度,速度大小没有改变,只是改变了速度的方向。外刃蹬地时的滑行轨迹是一段曲线。
3 外刃蹬地动作在转换到内刃蹬地的过程中也有自由滑进阶段
双蹬技术的外刃蹬地动作在转换到内刃蹬地的过程中也有不可忽略的从外刃支撑到平刃支撑的自由滑进阶段。这段过程包含在“外刃蹬地动作”的全部过程之中,占用了相当一部分时间,迫使外刃蹬地时必须提高支撑腿蹬地动作、摆动腿收摆动作的速度,用与传统滑行技术收摆动腿动作一半的时间完成外刃蹬地动作、一半的时间完成收摆动腿动作。或者加大“外刃蹬地动作”在一个完整滑行动作周期中所占比重。
4 两腿交替支撑在地面滑行轨迹的夹角
轮滑运动直道前滑的总运动方向是左、右两腿交替支撑滑行的合运动方向。根据轮滑运动的基本运动力学原理,支撑反作用力推动身体重心向侧移动,左右两腿交替支撑滑行时身体重心的移动轨迹是围绕总运动方向y轴左右S形曲线往复穿行,两腿交替支撑在地面滑行轨迹与总运动方向夹角越大、直线性越差、效率越低(见图2)。

图2 双蹬技术外刃蹬地动作受力分析原理图
可近似地计算水平面上滑行轨迹与总运动方向的夹角。以向侧蹬地时间t=1s为例,假设运动员惯性滑行速度v=10m/s,质量m=50kg,支撑反作用力F=490N,匀加速,空气阻力、地面摩擦阻力、轴承摩擦阻力忽略,内刃蹬地时支撑腿向侧倾斜与地面夹角γ=50°,根据公式水平分力:
F水=Fcosγ=314.9N
(2)
产生侧向水平加速度:
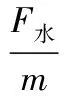
(3)
1 s时身体重心侧向移动速度:
v侧=vt=v0+a侧t=6.30m/s
(4)
因为轮滑运动蹬地动作的方向与支撑腿滑行方向相垂直,根据运动的合成与分解的平行四边形定则,1 s时合速度:
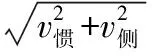
合速度与原惯性速度夹角:

假设外刃蹬地时支撑腿向侧倾斜与地面夹角θ=70°,根据公式水平分力
F水=Fcosθ=167.6N
产生侧向水平加速度:
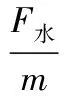
1 s时身体重心侧向移动速度:
v侧=vt=v0+a侧t=3.35m/s
1 s时合速度:
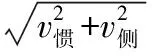
合速度与原惯性速度夹角:

运动员用传统技术的滑行轨迹与总运动方向夹角:
∠α/2=32°/2=16°
运动员用双蹬技术滑行的轨迹与总运动方向夹角:
(∠α+∠β)/2=(32°+18°)/2=25°
但是,因为外刃蹬地后并没有交换支撑腿、把身体重心推到新的支撑腿上,沿着合速度方向前进,而是进入外刃支撑转变平刃支撑过程,所以还是在惯性速度和向心力的作用下,沿着切线方向前进。以支撑时间t=1s为例,假设运动员惯性滑行速度v=10m/s,质量m=50kg,支撑反作用力F=490N,外刃蹬地时支撑腿向侧倾斜与地面夹角θ=70°,根据曲线运动向心力公式:
F向=F水=Fcosθ=167.6N

(6)
角速度公式:
(7)
双蹬技术外刃蹬地时运动员将在半径29.8m的曲线上以线速度10m/s、角速度0.336rad/s向前外侧偏离前进方向转弯滑去。
根据角速度公式:
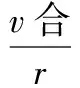
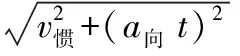
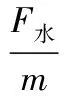
可见外刃蹬地时支撑腿向外倾斜程度越大、支撑反作用力越大角速度越大,直线性越差、前进效率越低。
5 外刃蹬地时支撑腿不可能向外倾斜很大
双蹬技术外刃蹬地时支撑腿向侧倾斜程度不可能很大。单腿支撑、向外侧倾斜,表面上看身体重心的投影点似乎移出了支撑面,但仅仅通过人体内力改变身体姿态就可使重心回到支撑面上方[5],一定是身体重心离开支撑面的距离很小或就在支撑面之内。假设外刃蹬地时支撑腿向侧倾斜程度比较大、动态支撑反作用力也比较大,就会使身体重心获得较大的水平方向加速度,如果没有交换支撑腿、没有第二个支撑点、没有其它的外力作用,会沿着惯性方向远离支撑点继续运动下去,不会向相反方向摆回到支撑面之内,当线速度明显下降时就会失去平衡向倾斜方向摔倒。而要使身体重心回到支撑面之内就需要一个方向相反的力,产生反方向的加速度来克服惯性,使身体重心向外侧运动的速度减小、消失,并向反方向再加速,这是需要较大的力和较多的时间的。以右脚为参考系,从右脚外刃蹬地身体重心向外侧运动开始到返回支撑点上方所做的功:
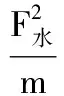
(8)
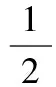
6 外刃蹬地动作在水平方向上做功的效率很低
根据前面的推论,运动员外刃蹬地时支撑腿向侧倾斜程度不大。假设运动员内刃蹬地时支撑腿最大倾斜程度可以达到与地面夹角γ=50°,外刃蹬地时支撑腿最大倾斜程度可以达到与地面夹角θ=70°,质量m=50kg,支撑反作用力F=490N,内刃蹬地时的侧向水平加速度6.30m/s2,外刃蹬地时的侧向水平加速度3.35m/s2。外刃蹬地时的侧向水平加速度是内刃蹬地时的53%,运动员做同样的功,外刃蹬地产生侧向水平加速度的效率仅是内刃蹬地时的53%。轮滑运动双蹬技术外刃蹬地做功中有用功效率可以用三角函数值表示η=cosθ。
7 外刃蹬地时的动力性支撑力不可能很大
假设运动员外刃蹬地时支撑腿向侧倾斜与地面夹角θ=70°,支撑反作用力的竖直向上分力根据公式F竖=Fsinθ,三角函数值大约是0.94。如果支撑反作用力很大会产生较大的加速度,当F竖/m>g的时候会使运动员跳起来,支撑腿跳离地面。双蹬技术的外刃蹬地动作从外刃开始支撑到结束到转变成内刃支撑,支撑脚没有离开地面,说明支撑反作用力产生的加速度不大。所以,外刃蹬地虽然是动力性工作,但因加速度不大,还是更趋近于静力性工作。
8 外刃蹬地时的支撑反作用力指向总运动方向的侧后方
假设右脚外刃蹬地滑行的轨迹是圆上的一段弧,把圆放入笛卡尔直角坐标系中,以圆心为坐标原点,以直道前滑总运动方向为y轴,过圆心横线为x轴,只有轨迹处于第Ⅲ象限时惯性运动方向有指向y轴正值的分运动,同时支撑反作用力有指向y轴正值的分力、可以在总运动方向上产生加速度(见图3)。但右脚外刃蹬地滑行的轨迹处于第Ⅲ象限的前提是左脚内刃蹬地时的支撑反作用力产生的速度与惯性速度的合速度指向左外侧,这将导致左脚内刃蹬地时的惯性速度方向严重偏离总运动方向y轴,前进效率大大降低。
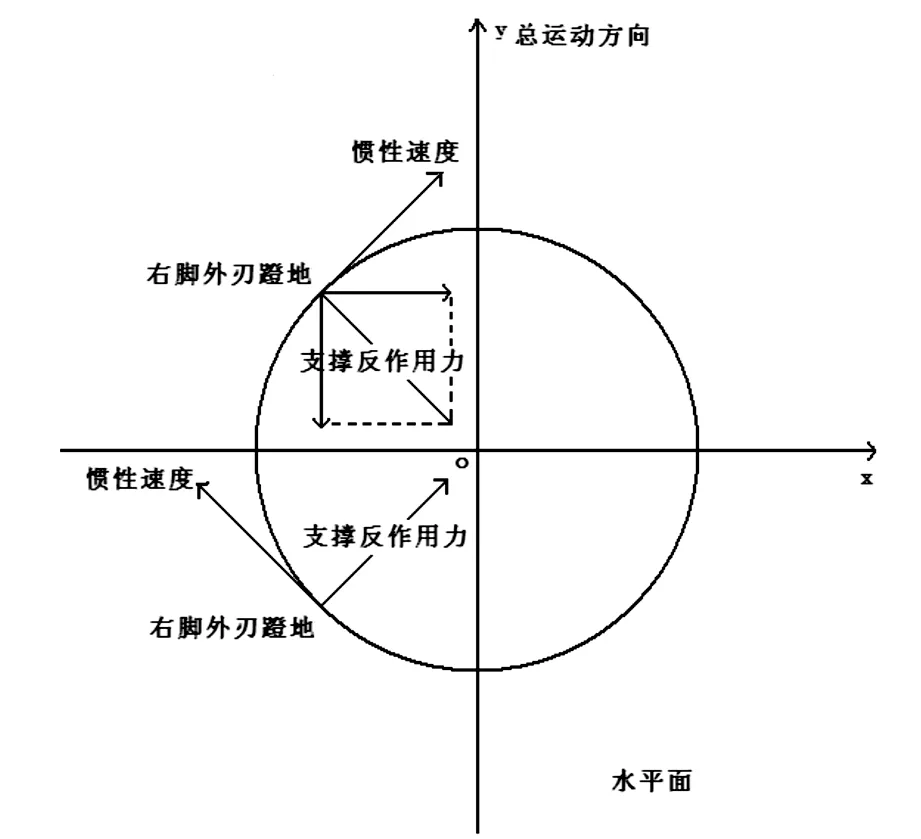
图3 假设右脚外刃蹬地滑行轨迹图
右脚外刃蹬地时的滑行轨迹实际上是处于直角坐标系的第Ⅱ象限里。因为直道前滑左脚内刃蹬地时惯性速度的方向是指向左前方的,在摆动腿刀尖方向应与支撑腿向侧蹬地的支撑反作用力产生的速度和惯性速度的合速度方向平行的前提下,只要左脚内刃蹬地时的合速度方向是指向总运动方向y轴的时候,根据图2,右脚外刃蹬地时的滑行轨迹就是在直角坐标系的第Ⅱ象限里,右脚外刃蹬地时的支撑反作用力方向就是指向总运动方向的侧后方的。将右脚外刃蹬地时的支撑反作用力在水平面上分解成与总运动方向y轴平行的力和垂直的力,与总运动方向y轴平行的力产生的加速度为负值。同理,左脚外刃蹬地时的滑行轨迹处于直角坐标系的第I象限里时支撑反作用力与总运动方向y轴平行的分力产生的加速度为负值。
9 结论
轮滑运动双蹬技术的外刃蹬地动作只能在水平方向上产生一个不大的与总运动方向相反的加速度。
[1] 于立强,孙维民,王焕.轮滑教育[M].长春: 吉林科学技术出版社,2008:46,32,38,49.
[2] 孙显墀,孙一.对速度轮滑直道双蹬技术的探讨[J].冰雪运动,2006(6):29-31.
[3] 常莉彬.对速度轮滑双蹬技术结构的分析[J].吉林体育学院学报,2006(1):58-59.
[4] 刘静春,费瑛.对速度轮滑双蹬技术的认识[J].吉林体育学院学报 2008,24(6):45-46.
[5] 体育学院通用教材运动生物力学编写组.运动生物力学[M].北京:人民体育出版社,2007:63,107.
AnalysisontheAccelerationProducedbytheOuter-edgePushinDouble-pushTechniqueofSlide
Liu Feng1,Guan Ruhua2
(1.College of Physical Education,Jilin University,Changchun,130012,Jilin,China; 2.College of Mathematics,Jilin University,Changchun,130012,Jilin China)
The mathematical deduction has been applied to investigate if the outer-edge push in double-push technique can efficiently accelerate forward in slide.The results demonstrate that it can produce a slight lateral force,being true of the centripetal force in cure movement.When the curve track for right feet locates in the second quadrant,or that for left feet locates in the first quadrant of the rectangular coordinate system using moving direction as y-axis,the force will be opposite to the moving direction,and thus no positive contribution can be achieved.Therefore,the slight acceleration in apposite to the moving direction will be produced by the outer-edge push in double-push technique.
double-push technique;standing leg;outer-edge push;cline;speed;acceleration;direction
G862.8
A
1672-1365(2011)06-0066-03
2011-07-16;
2011-09-15
刘锋(1961-),男,吉林长春人,副教授,研究方向:体育教学与训练。

