类比思想在数学解题中的应用误区

●

(杭州外国语学校 浙江杭州 310023)

类比思想在数学解题中的应用误区

●赵肖东

(杭州外国语学校 浙江杭州 310023)

类比推理是由2类对象具有某些相似特征和其中一类对象的某些已知特征，推出另一类对象也具有这些特征的推理(简称类比).在数学中，可以由已经解决的问题和已经掌握的知识出发，通过类比推理提出新问题和作出新发现.数学家波利亚曾指出“类比是一个伟大的引路人”.高中数学新课标把培养学生的类比推理能力作为主要的能力培养目标之一.类比在发展学生创新精神的过程中有着无可比拟的价值.类比推理的创造性作用除了体现在发现新的命题，直至发现新的领域外,还可以用来发现解决问题的途径与方法.在解决数学问题中，为寻找问题的线索往往可借助类比的方法，在类比的应用过程中，往往与解题者原有知识、经验中类似形式或结构、类似方法或模式有联系.类比含有猜测的成分，是或然推理，属于合情推理的范畴，在数学思维中正是这种局限性导致学生在学习新知识、解决新问题过程中产生错误.本文试图通过一些例子来探讨类比推理在数学解题中的使用误区.

1复数与实数的类比

在高中数学中，数的概念从实数集扩充到复数集后，其基本运算性质和实数的运算性质相类似，但是有些实数集中的性质就丧失了，譬如实数集中的有序性、平方的非负性等，此时再用实数集中的老办法解决复数集中的新问题，就容易导致错误.

案例1

分析类比实系数一元二次方程，利用判别式判断方程根的个数的方法来讨论复系数方程根的情况是错误的.实系数一元二次方程ax2+bx+c=0，配方得

正解设x0为其实根，则

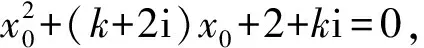
即

于是

2向量与数量的类比

高中课程类比数量引入向量的概念，向量不同于数量，向量有方向，而数量的代数运算在向量范围内不都适用，因此若将向量运算和数量运算简单作类比，则有可能导致错误.

案例2

已知a，b，c是非零向量，a⊥b，x∈R，x1，x2是关于x的方程ax2+bx+c=0的2个解，求证：x1=x2． 已知x1，x2是关于x的方程ax=b(a≠0)的2个解，求证：x1=x2．方程两边同乘非零向量b，则b·(ax2+bx+c)=0，即b·ax2+b2x+b·c=0．因为a⊥b，所以方程可化为b2x+b·c=0．方程两边同乘1a，得x=-b·cb2，从而x1=x2．得x=ba，所以x1=x2．

分析实系数方程同解原理：在实系数方程中,2边同乘非零常数，解集不变.但是将向量方程的2边同时乘非零向量b却不是同解变形.因为由b与ax2+bx+c垂直也可得b·ax2+b2x+b·c=0,所以b·ax2+b2x+b·c=0的解不一定是ax2+bx+c=0的解.

正解由题意得

两式相减得

(x1-x2)[(x1+x2)a+b]=0.

因为a⊥b，所以(x1+x2)a⊥b，得

(x1+x2)a+b≠0,

故x1=x2.

3空间与平面的类比

把立体几何知识与相关的平面几何知识类比，是实现知识迁移的一种有效方法，同时也可以简化运算与推理，从而优化解题过程.但是平面几何中的定义、定理对于空间图形不一定成立，因此两者类比可能导致错误.

案例3

分析在平面几何中有平行四边形的判定定理：2组对边分别相等的四边形是平行四边形.而在空间中，这个定理并不正确.因此该题的证明是错误的.

正解如图3，在DD1上取DG=AE.由DG=AE,DG∥AE,得四边形CGEB是平行四边形，因此

CG=BE，CG∥BE.

从而易得△C1D1F≌△DCG(SAS)，于是

CG=D1F,CG∥D1F,

因此

BE=D1F,BE∥D1F,

图3

故四边形BFD1E是平行四边形.

4圆锥曲线与圆的类比

圆是圆锥曲线中最基本、最简单的一种图形，与圆锥曲线在定义和几何性质方面有很多的相似性，但由于各类曲线的差异性、特殊性，若都套用圆的解题模式，则失误必然难免.

案例4

判断下列椭圆和圆的位置关系：x2+2y2=8，x2+(y+2)2=4． 判断下列两圆的位置关系：x2+y2+2x+8y-8=0，x2+y2-4x-4y-2=0．联立方程x2+2y2=8；x2+(y+2)2=4，{(1)联立方程x2+y2+2x+8y-8=0；x2+y2-4x-4y-2=0，{(3)2式相减消去x，得y2-4y-8=0．(2)2式相减化简得x+2y-1=0(4)再代入式(3)消去y得x2-2x-3=0，(5)由Δgt;0，得方程(2)有2个不同的解，则椭圆与圆有2个交点．由Δgt;0，得方程(5)有2个不同的解，则两圆有2个交点．

分析因为式(3)等价于方程组

正解方程(2)有2个不同的解

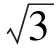
一般说来，当学生进入新知识领域时，常常会选择熟知的、有相似特征的旧知识和方法类比地对待新知识、新问题，寻求一条快捷的解决途径.但这有时会发生不易察觉的错误，上面这些例子就是如此.因此教师应采用多种方法和手段指导学生主动建构新知识，处理好新旧知识之间的联系和区别.用好类比这把双刃剑，对类比的过程要多加分析，去伪存真，这不但能获得新知识，而且更重要的是它对发展学生的创新能力有着极好的促进作用.