Regular范畴研究

任 芳

(福建船政交通职业技术学院基础部，福建 福州 350007)

Regular范畴研究

任 芳

(福建船政交通职业技术学院基础部，福建 福州 350007)

首先证明了Abel范畴是Regular范畴，然后证明了Regular范畴关于任意小范畴的函子范畴仍是Regular范畴。

Abel范畴； Regular范畴；Regular满态射；函子范畴

Abel范畴是一类性质较好的范畴，从范畴论产生至今，一直是诸多数学工作者致力研究的对象。H.Bass给出了Abel范畴等价于模范畴等的充要刻画[1]，N.Popescu则从一般环模理论的研究提升至Abel范畴，并给出丰富的应用[2]。粗略地说，Regular范畴是去掉加性而具有类Abel范畴正合结构的一类范畴，文献[3-5]对Regular范畴进行细致地研究与刻画。

扩张的研究历来是代数学研究的热点问题。函子范畴是范畴的一种扩张形式，诸多范畴经过函子范畴形式扩张之后具有原来不具备的良好性质。 P.Freyd、B.Mitchell等对预加范畴关于Abel群范畴的函子范畴的扩张进行细致而深入地研究，并给出该函子范畴的结构刻画与诸多同调性质[6-8]。 A.Neeman进一步将函子范畴的研究推向三角范畴层面，发展出以函子和函子范畴扩张方式研究三角范畴的研究方法[9]。下面，笔者基于扩张的思想，结合性质保持问题对Regular范畴展开研究。

1 相关概念及性质

定义1设A为一范畴，若一满态射为一对态射的差余核，则称该态射为Regular满态射。在Regular范畴中，以如下记号表示Regular满态射：

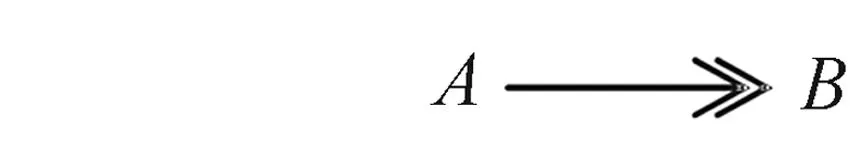
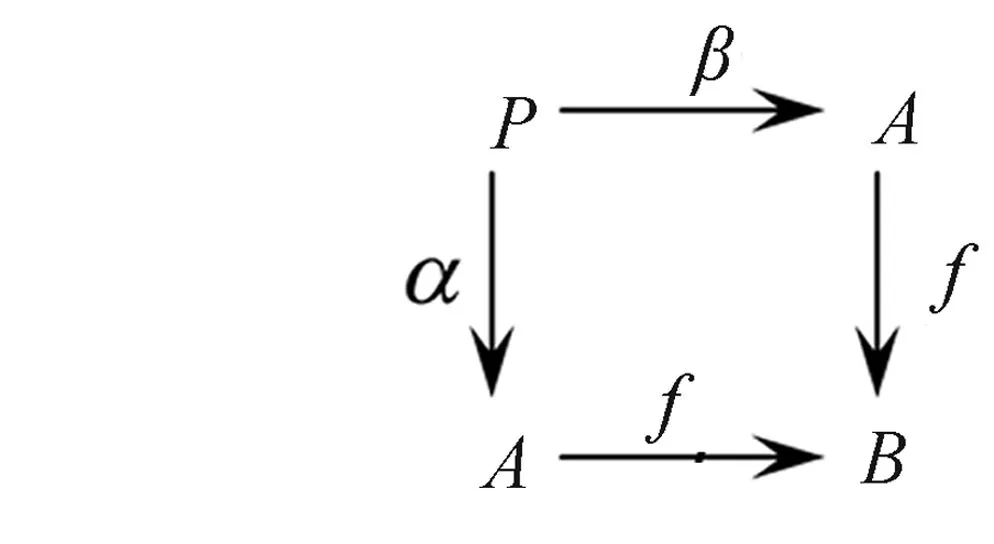
①一般地，拉回保持单态射，然而推出却不保持满态射；②核对中的态射α,β均为满态射；③容易证明如下命题等价：(i)态f为单态射；(ii)态射f的核对存在，且为(A,1A,1A)；(iii)态射f的核对存在，且有α=β。

定义3一个范畴称为Regular范畴当且仅当其满足以下条件：①每一个态射有核对；②每一个核对有差余核；③每一个Regular满态射关于任意态射的拉回仍是Regular满态射。

2 Regular范畴与Abel范畴

引理1差余核是其核对的差余核，核对的差余核是该差余核的核对。

证明只证明第1个命题，第2个命题类似可证。设态射f:A→B为态射对α,β:X→A的差余核，

考察如下交换图：

由核对的泛性知，存在唯一的态射z:X→P使得如上交换图可交换。

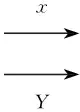
定理1Abel范畴是Regular范畴。

证明记A为一Abel范畴，任取一态射f，考虑如下态射的交换图：

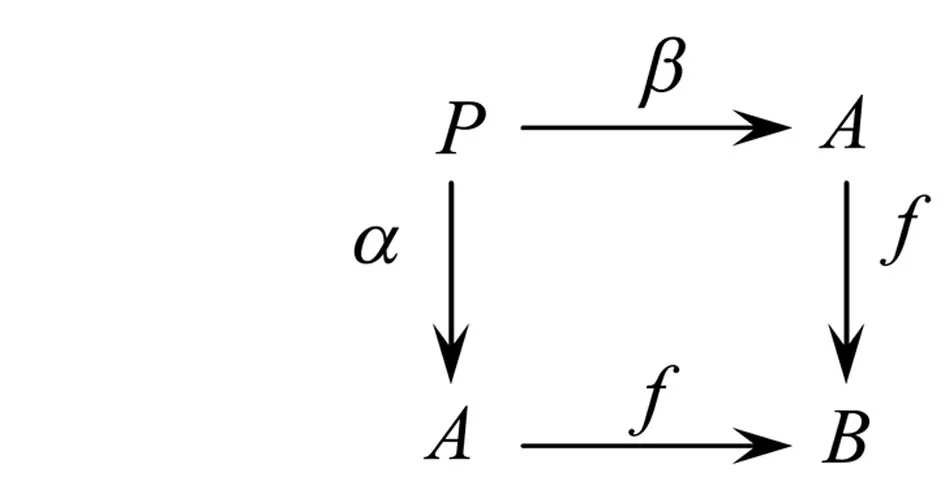
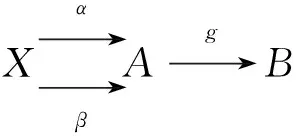
最后证明拉回保持Regular满态射。考察下述拉回图：

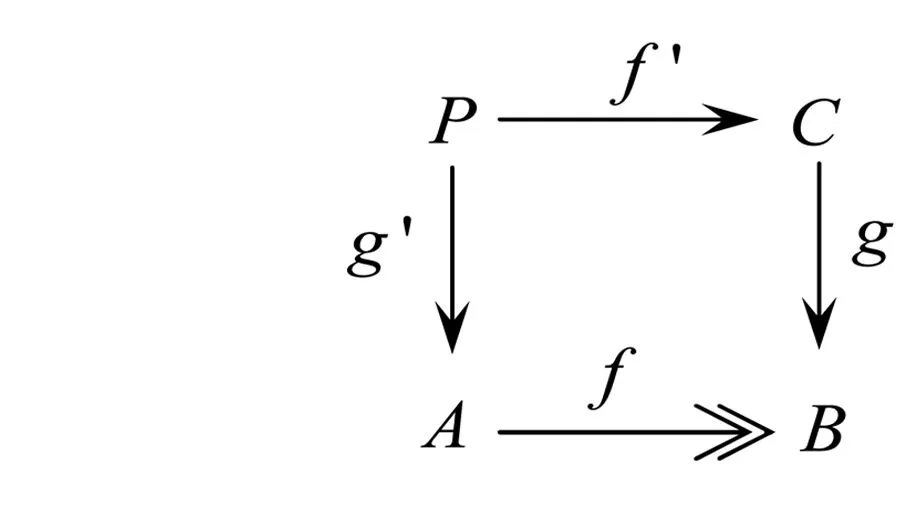
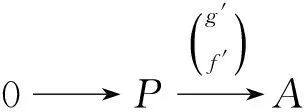
再据推出的等价定义知

为推出图。由Abel范畴的推出的性质，有Cokerf=Cokerf′(同构)。故f′亦为满态射。

因为态射f′具有核对，据引理1，有f′为Regular满态射。此即说明Regular满态射在拉回意义下是稳定的。

3 Regular范畴的函子范畴

定理2Regular范畴的函子范畴仍是Regular范畴。

证明记A为一Regular范畴，C为一小范畴。考察函子范畴Fun(C,A)，任取一自然变换σ:F→G，对于任意的态射f:A→B，考察如下交换图：

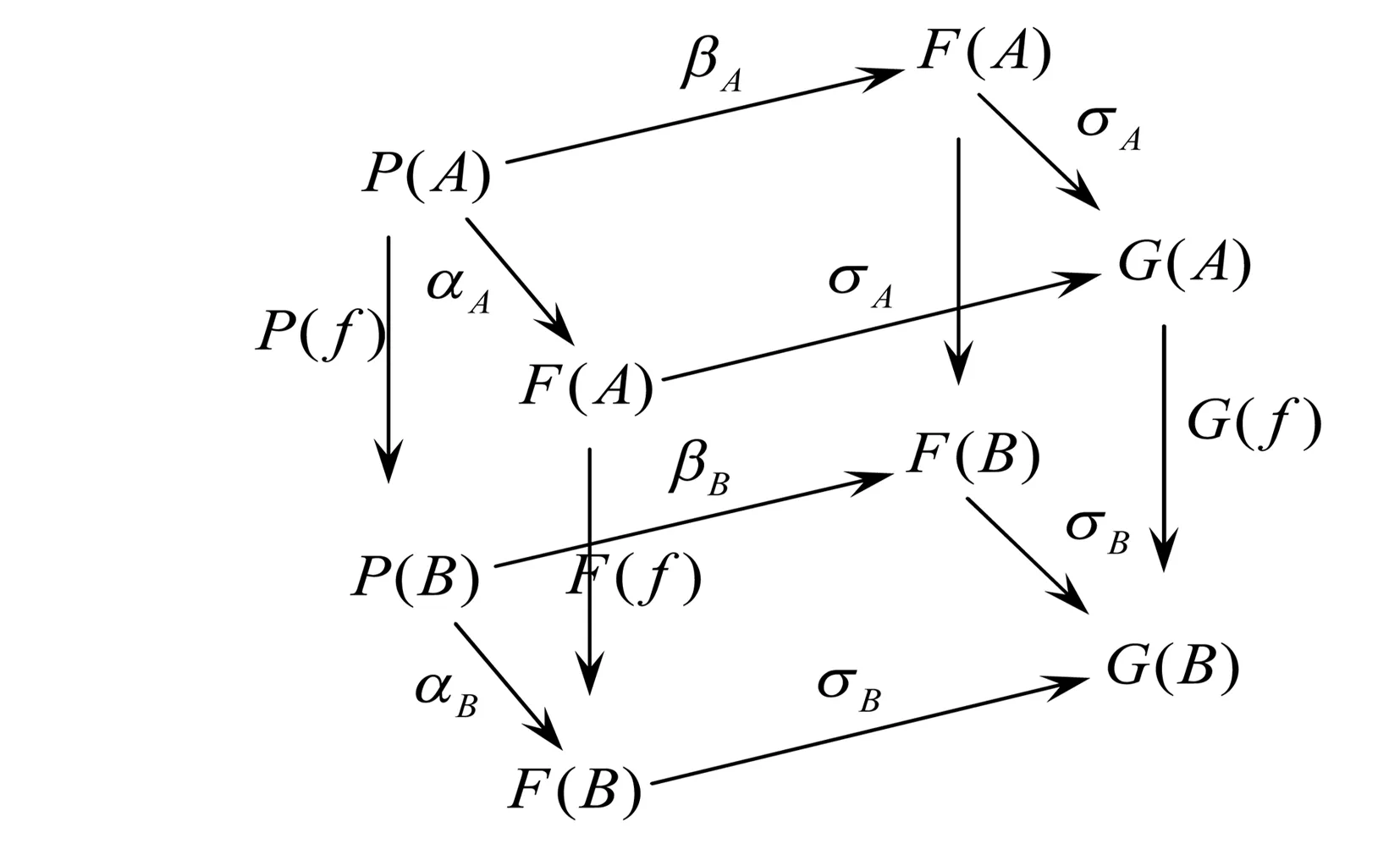
由于A为Regular范畴，故对于每一个对象A∈A，σA:F(A)→G(A)有核对。

定义P:C→A，其中P(A)为σA:F(A)→G(A)对应的核对对象；对任意态射f:A→B，由于σBF(f)αA=G(f)σAβA=σBF(f)βA,据核对的定义知存在唯一的态射P(f)，使得上述态射图可交换。容易验证α={αA}A∈A,β={βA}A∈A为自然变换。故每一个自然变换具有核对。

不难类似证明每一个自然变换的核对具有差余核。最后证明拉回保持Regular满自然变换。为此，考虑Regular满自然变换σ:F→G与任意自然变换构成的拉回：

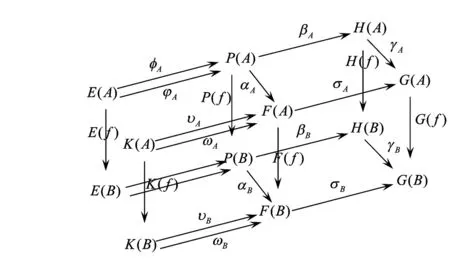
由于σ:F→G为Regular满自然变换，其是某一自然变换的差余核，据引理1知，σ:F→G为其核对υ,ω:K→F的差余核。由于范畴A为Regular范畴，故对于每一个对象A∈A，态射βA：P(A)→H(A)。为某一态射对的差余核。再据引理1知，βA：P(A)→H(A)为其核对φ，φ：E(A)→P(A)的差余核。由于βBP(f)φA=H(f)βAφA=βBP(f)φA，故存在唯一的态射E(f)使得φBE(f)=P(f)φA，φBE(f)=P(f)φA。于是可以定义一个函子E:C→A，与自然变换φ={φA}A∈A，φ={φA}A∈A使得自然变换β:P→H。 为Regular满自然变换，至此定理2证毕。

[1]Bass H.Algebraic K-Theory[M].New York：Benjamin，1998.

[2]Popescu N.Abelian Categories with Applilcations to Rings and Modules[M].London & New York: Academic Press, 1973.

[3]Carboni A, Vitale E M.Regular and exact completions[J].J Pure Appl Alg, 1998，125:79-116.

[4]Lack S.A note on the exact completion of a Regular category and its infinitary generlizations[J].Theory and Applications of Categories, 1999, 5(3):70-80.

[5] Meisen J.Pullbacks in regualr categories[J].Canad Math Bull, 1973, 16(2): 251-255.

[6]Freyd P.Abelian Categories[M].New York: Harper and Row, 1964.

[7]Freyd P.Functor Categories and Their Application to Relative Homology[M].New York: Columbia University, 1962.

[8]Mitchell B.Rings with several objects[J].Adv Math, 1972, 8:1-161.

[9]Neeman A.Triangulated Categories.Annals of Mathematics Studies[M].Princeton:Princeton University Press, 2001.

[编辑] 洪云飞

10.3969/j.issn.1673-1409.2011.12.007

O154

A

1673-1409(2011)12-0016-03