导函数极限和连续的特殊性及其应用
王小强
(辽宁铁道职业技术学院基础部,辽宁 锦州 121000)
导函数极限和连续的特殊性及其应用
王小强
(辽宁铁道职业技术学院基础部,辽宁 锦州 121000)
导函数的极限和导函数的连续性,有着一般函数所不具备的特点。应用这些特点去研究和计算导数问题比用普通方法有着许多便利之处。对导函数的极限和导函数的连续性特点和应用给予了阐述和证明。
导函数;极限;连续

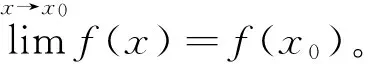
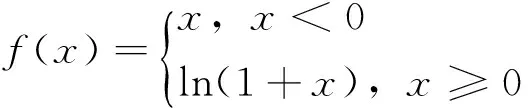
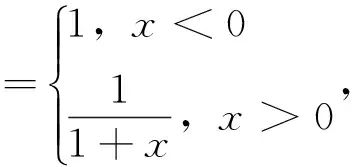
定理1还能说明:在满足函数f(x)在邻域U(x0,δ)内连续,且在邻域U(x0-δ,x0)及U(x0,x0+δ)内分别可导的条件下,导函数f′(x)在点x0处只要存在极限,则导函数f′(x)在该点处必然连续;反之,如果导函数f′(x)在一点连续,那么导函数f′(x)在该点处也必然存在极限。
推论1函数f(x)在邻域U(x0,δ)内连续,且在邻域U(x0-δ,x0)及U(x0,x0+δ)内分别可导,且f′(x)在点x0处极限存在是f′(x)在该点处连续的充要条件。
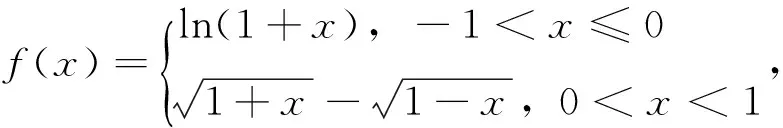

推论2函数f(x)在邻域U(x0,δ)内连续,且在邻域U(x0-δ,x0)及U(x0,x0+δ)内分别可导的条件下,导函数f′(x)只能存在跳跃型间断点和第二类间断点。
以上各个命题和推论中的结论在一般的函数上肯定是不成立的。因此这些都是导函数的特点。而且通过以上2个例子可以看到利用这些特点来研究和计算导数问题的便利之处。
定理2设函数f(x)在邻域U(x0,δ)内连续,且在邻域U(x0-δ,x0)及U(x0,x0+δ)内分别可导,且点x=x0是导函数f′(x)的跳跃型间断点,则f(x)在点x=x0处必不可导。


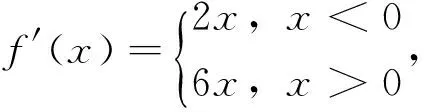
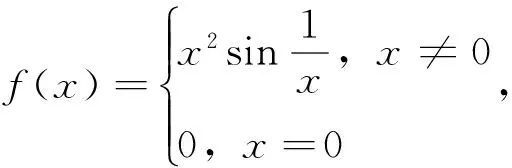

例4是在导函数f′(x)间断点x=x0处f′(x0)存在的典型例子。在函数f(x)在邻域U(x0,δ)内连续,且在邻域U(x0-δ,x0)及U(x0,x0+δ)内分别可导的条件下下,只有在f′(x) 的第二类间断点处才可能出现这种情况。
[1]同济大学数学系.高等数学[M].北京:高等教育出版社,2007.
[2]王学理,孔庆海.高等数学全析全解[M].沈阳:东北大学出版社,2011.
[3]李正元.高等数学辅导[M].北京:国家行政学院出版社,2008.
[编辑] 洪云飞
10.3969/j.issn.1673-1409.2011.12.005
O175.1
A
1673-1409(2011)12-0012-02

