不动点定理的相关应用
刘 波, 李承耕
(韩山师范学院数学与信息技术系, 广东 潮州 521041)
不动点定理的相关应用
刘 波, 李承耕
(韩山师范学院数学与信息技术系, 广东 潮州 521041)
主要介绍了Banach 不动点理论及其在数学分析、积分方程、微分方程中的应用,应用不动点理论证明了闭域套定理、积分方程和微分方程解的存在唯一性。
不动点;不动点定理;应用
1 Banach不动点定理
定义1[1]设X是给定的集合,T:X→X为X到自身中的映射,如果∃x0∈X使得Tx0=x0,则称x0为映射T的一个不动点。
定义2[2]设X=(X,d)是度量空间,T是X到X中的映射,如果存在一个数a,0
d(Tx,Ty)≤αd(x,y)
(1)
则称T是压缩映射。
定理1[3]设X=(X,d)是完备的度量空间,T是X上的压缩映射,那么T有且只有一个不动点。
2 闭域套定理的证明

证明设{Dn}是R2中的闭域列,p1,p2是闭域Dn中的2个点,坐标为p1(x1,y1),p2(x2,y2),定义距离d(p1,p2)=|x1-x2|+|y1-y2|,则闭域Dn显然是完备的度量空间。
对∀p(x,y)∈Dk,设ak=min{x|(x,y)∈Dk},bk=max{x|(x,y)∈Dk},ck=min{y|(x,y)∈Dk},dk=max{y|(x,y)∈Dk},作映射:
对∀p(x,y)∈Dk,有Tp(Dk)⊂Dk,所以Tp是Dk到自身的一个映射。
现证T是压缩映射,任取p1,p2∈Dk,满足:
“你小子呀,总算来了。”小表姐杨晓梅把两盘菜放在餐桌正中间,“你快坐下吧。你们娘俩多亲近,我这还有两个菜,你们先吃着,我就来。”
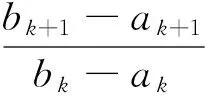
由于Dk+1⊂Dk,所以:
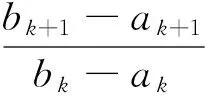
令:
得到:
d(Tp1,Tp2)≤αd(p1,p2)
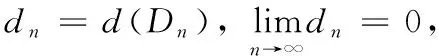
3 积分方程解的存在唯一性
定理3设f(x)为a≤x≤b的连续函数,k(x,t)为正方形a≤x≤b,a≤t≤b上的连续函数。若存在常数M使得:

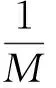


由于α=|λ|M(b-a)<1,所以T是C[a,b]到C[a,b]的一个压缩映射,由Banach不动点定理,存在一个不动点满足方程。
4 微分方程解的存在唯一性
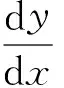

[1]张恭庆,林源渠.泛函分析讲义(上册)[M].北京:北京大学出版社,1998.
[2]程其襄.实变函数与泛函分析基础[M].北京:高等教育出版社,2003.
[3] 薛昌兴. 实变函数与泛函分析[M]. 北京:高等教育出版社,2004.
[编辑] 洪云飞
10.3969/j.issn.1673-1409.2011.12.006
O177.2
A
1673-1409(2011)12-0014-02

