孔底轴向水介质不耦合效应的数值模拟

钱立坤,林大能,刘医硕,龙 专

(湖南科技大学能源与安全工程学院, 湖南湘潭市 411201)

孔底轴向水介质不耦合效应的数值模拟

钱立坤,林大能,刘医硕,龙 专

(湖南科技大学能源与安全工程学院, 湖南湘潭市 411201)

运用非线性有限元软件 ANSYS/LS-DYNA对耦合装药和孔底水不耦合装药 2个模型孔底起爆进行计算,对计算结果进行对比分析发现:不耦合装药在模型底部由于水的缓冲作用使得应力、有效应力、最大剪应力、最大主应力峰值较小,但振动加速度、振动速度以及合成位移的峰值较大加速了裂隙的形成和扩展,改变了能量的做功效果,有利于孔底岩石的破碎;在模型的上部与耦合装药监测到的结果较为类似,孔底水不耦合装药对本模型上部炮孔的爆破效果影响甚微。

条形药包;轴向不耦合装药;水介质不耦合装药;数值模拟

0 引言

炮孔中的炸药装药结构大致可分为 2种,耦合装药与不耦合装药。不耦合装药又可分为径向与轴向不耦合,不耦合介质常见的有空气和水。不耦合装药能达到耦合装药的相似效果,且同时减少了炸药消耗量和爆破器材的消耗,能提高工作效率有效节省爆破成本[1]。一批工程技术人员、学者、专家对不耦合装药的理论计算[2～4]、工程应用[5,6]、试验研究[7]以及数值模拟[8～10]方面做出了行之有效的工作,研究主要集中在孔壁的初始应力求解和寻求最佳不耦合系数,运用数值模拟软件能动态地观察爆轰波分布,再现爆轰短暂的过程。文章拟从应力、有效应力、最大剪应力、最大主应力、振动加速度、振动速度、合成应变几个方面通过对比,分析耦合装药与水不耦合装药的异同,以期得出有益的结论。

1 数值模拟计算

1.1 计算模型

文章中计算了 2个模型:轴向不耦合模型由炸药、水、岩石 3个部分组成(见图1);耦合模型由炸药、岩石 2个部分组成,即将图1 中的水柱换做岩石。2个模型均选用实体单元 solid164进行建模和拉格朗日网格划分,单元使用多物质 ALE算法。从孔底起爆,为模拟条形药包在半无限介质中爆轰,所以对模型 2个对称面施加法向约束,侧面和底面施加无反射边界条件,顶部为自由面。

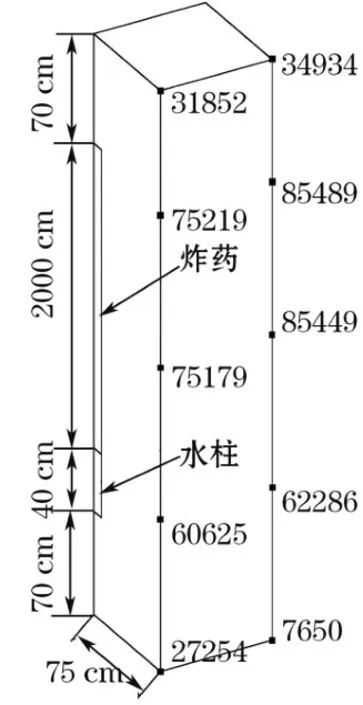
图1 模型及检测节点位置

由于模型的对称性,且为节约计算时耗,建立四分之一模型。一些学者[11,12]通过计算发现爆轰冲击波、爆生气体、孔腔压力持续时间为数百微秒,所以本模型计算时间确定为 2000μs。模型采用 LSDYNA 970进行求解,使用 LS-PREPOST 1.0进行后处理。模拟时采用 cm-g-μs单位制。炸药使用 2#岩石乳化炸药。

模型长、宽各 75 cm,高 380 cm;条形药包长、宽各 10 cm,装药高 200 cm;水柱高 40 cm,长 、宽各 10 cm。

1.2 材料模型和计算状态方程及参数

模拟中选用 2#岩石乳化炸药,采用 ANSYS/LS-DYNA程序提供的高能炸药材料模型MAT_H IGH_EXPLOS IVE_BURN和爆生气体压力-体积关系的状态 JWL方程来计算[13]。

式中,A、B、R1、R2、ω为材料常数,P为压力;V为爆轰产物相对体积;E为爆轰产物初始内能密度。输入参数见表1[14]。

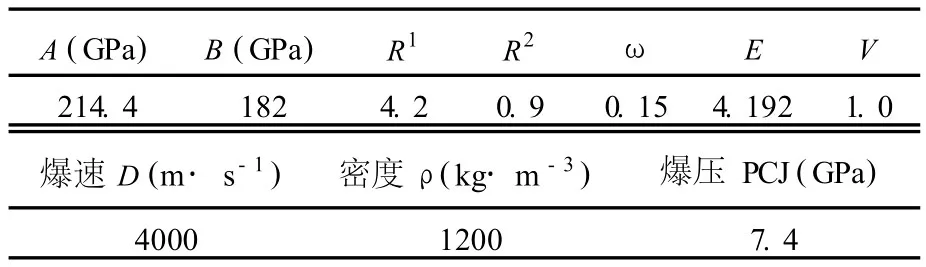
表1 2#岩石乳化炸药材料参数及 JWL状态方程参数

水的材料模型采用的是 ANSYS/LS-DYNA中给出的 Null空材料模型,运用 Gruneisen状态方程进行计算。该状态方程可通过 2种方法定义压力体积的关系,从而确定材料是压缩还是扩张。具有立体撞击速度——粒子的 Gruneisen状态方程[15]定义压缩材料的压力如下:

式中,C是 vs-vp曲线[15]的截距;S1,S2、S是vs-vp曲线的斜率系数;γ0是 Gruneisen常数;a是γ0和μ=的一个体积修正量;ρ0为材料的初始密度;E为初始能量密度。状态方程的输入参数见表2[16]。

表2 水的参数及 Gruneisen状态方程参数

模型中的被爆岩石采用 ANSYS/LS-DYNA提供的MAT_PLASTI C_K INEMATIC塑性随动模型。此模型不但考虑了模型的同性、随动硬化且考虑了应变率,同时也考虑了失效。通过调节β的值(0≥β≥1),来调节各向同性或随动硬化[16]。应变率用Cowper-Symonds模型来考虑,用与应变率有关的因数表示屈服应力。

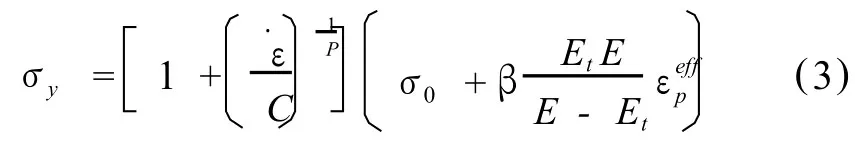
式中,σ0为初始屈服应力,Pa;为应变率,s-1;C和P为 Cowper-Symonds应变率参数;为有效塑性应变;E为材料弹性模量,Pa;ET为材料切线模量,Pa;模型参数见表3[14]。

表3 矿体塑性动力学模型材料参数

2 计算结果及分析

2.1 应力云图及分析

炸药在开始爆轰时产生的冲击波以球状向周围介质传播,在消耗了一定的能量后衰减为应力波,最后随着应力波能量的进一步衰减成为地震波。图2和图3分别显示了 4个不同时刻轴向水不耦合、耦合孔底起爆的应力云图。2模型的炸药起爆时间均设置在 0μs,开始起爆后到 100μs左右应力的云图出现了明显的不同,不耦合装药的最大值小于耦合装药;而后,应力波以“纺锤形”继续向孔口传播,在孔底附近首次产生了应力集中现象,见图2(BO-2)、图3(OH-2),同时由于自由面的反射作用,在孔口附近也出现了应力集中;随着应力传播、能量衰减在图2(BO-3)和图3(OH-3)的时刻孔口附近出现应力集中核;最后应力集中现象再次在孔底出现,见图2(BO-4)和图3(OH-4)。

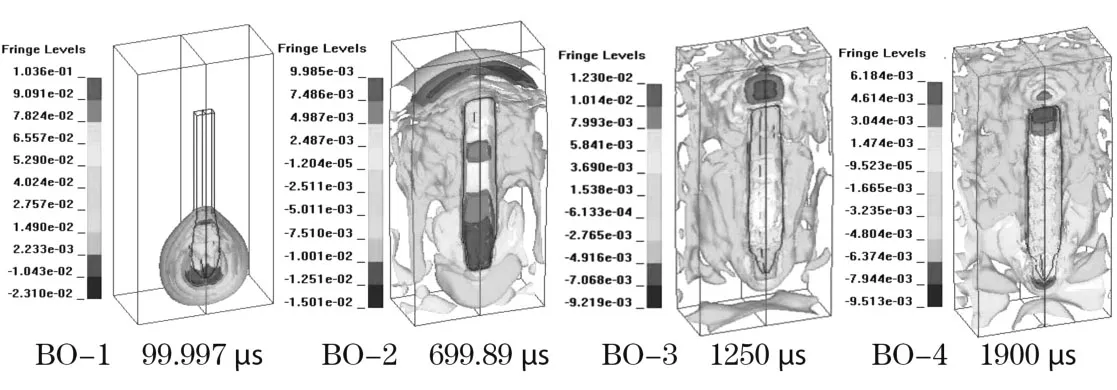
图2 孔底轴向水不耦合孔底起爆不同时刻的应力云图

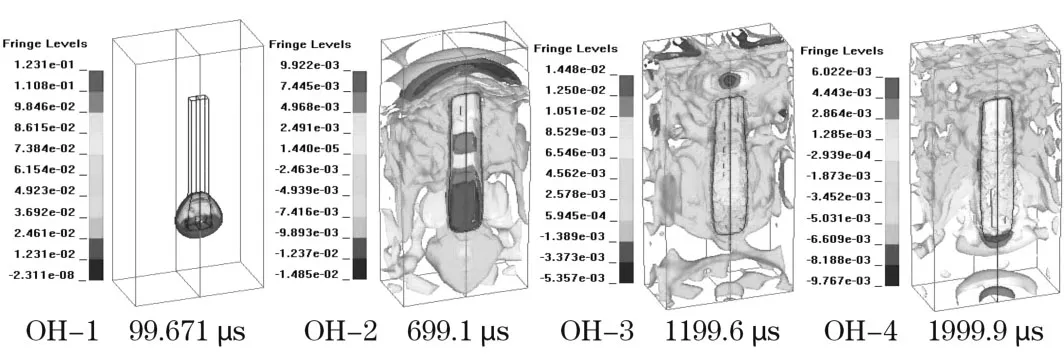
图3 耦合装药孔底起爆不同时刻的应力云图

2.2 节点的检测及其分析

为了比较轴向不耦合装药与耦合装药时的差别,分别在 2个模型高度的 0,100,200,300,380 cm处选取如图1 所示的 10个点作为检测对象,对同一处节点单元的压力、有效应力、最大主应力、最大剪应力、质点的振动加速度、振动速度进行作图对比分析,并找出具有代表性的点进行分析。

(1)压力。从图4中可以看出耦合装药条件下,模型底部点 60625的应力开始作用时间和峰值均较大,应力的峰值近 0.35 MPa。而不耦合装药的峰值压力只有近 0.005 MPa。模型中部点 85449不耦合装药的峰值较大,也达到了近 0.35 MPa,但耦合装药压力开始作用的时间较早。

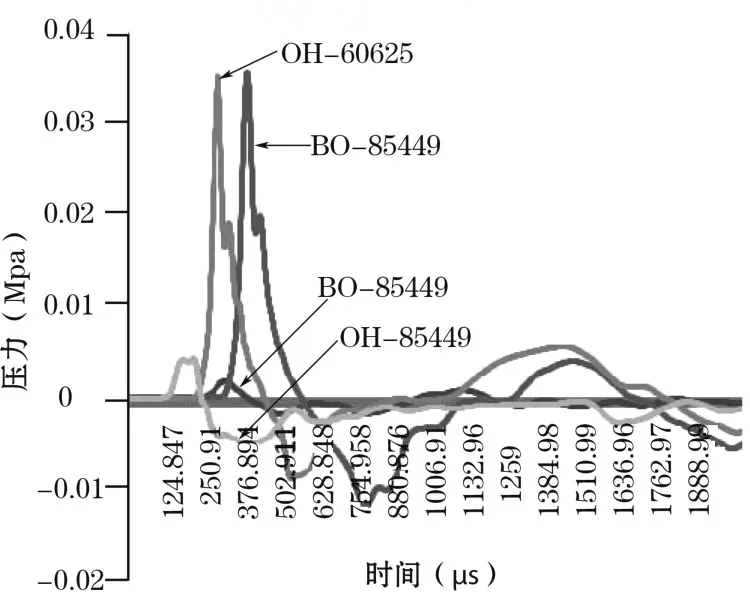
图4 压力时程曲线

(2)有效应力。如图5所示,在点 60625的比较中,耦合装药有效应力的曲线大部分在不耦合装药的上方,且峰值较大,峰值和谷值差值较大,不耦合装药的峰值较小,变化范围也较小。点 85489不耦合装药的曲线大多数情况在耦合装药曲线之上,虽然其峰值较大,但变化范围较小,较为平稳,耦合装药的情况则反之。

图5 有效应力时程曲线

(3)最大剪应力。图6为最大剪应力时程曲线。耦合装药条件下的 OH60625曲线,其最大峰值达到了 0.006 MPa以上,不管是开始作用的时间还是峰谷值之差均大于 BO60625曲线,但曲线BO60625显得较为缓和平稳。对于点 75219来说,不耦合装药产生的峰值较大,且曲线的频率变化较快,耦合装药的曲线却显得较为平稳频率变化较小。

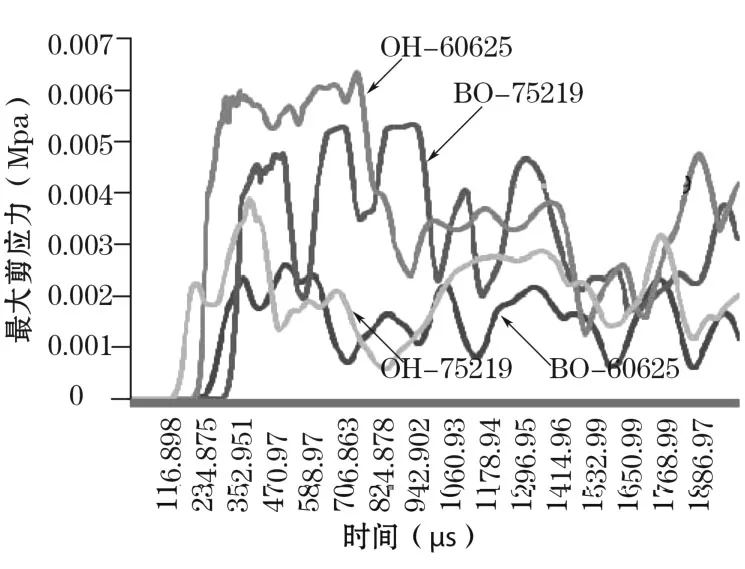
图6 最大剪应力时程曲线

(4)最大主应力。如图7所示,点 27254在耦合装药情况下,在负方向产生了较大的主应力,超过了 0.03 MPa,在正方向产生的主应力值也较大接近0.0125 MPa,且开始作用的时间较不耦合装药早。对于点 85489来说不耦合装药开始作用时间晚于耦合装药,但正负方向的峰值均大于耦合装药。

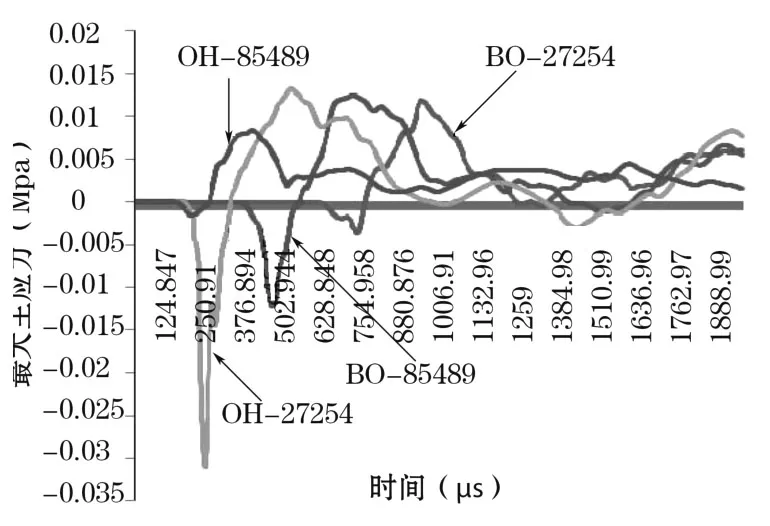
图7 最大主应力时程曲线

(5)振动加速度。从图8中可以看出,点31052耦合装药和不耦合装药的振动加速度曲线几乎完全重合,这说明 1.2的装药不耦合系数对此质点的振动加速度几乎没有影响。点 27254在 2种装药方式下总体趋势较为类似,但在耦合装药方式下,其峰值较大但振动开始作用时间稍短。

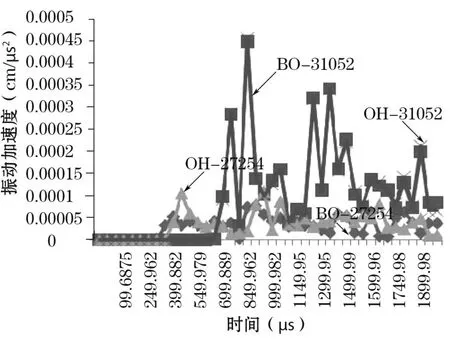
图8 振动加速度时程曲线

(6)振动速度。在图9中,点 7650在不耦合装药情况下,开始振动的时间稍早于耦合装药的情况,峰值也稍大两曲线的走向和趋势都较为类似,但曲线 75179在 2种装药情况下开始部分几乎完全重合,其最大值都达到了约 0.0225 cm/μs,其余部分的主要趋势和走向大致相同。

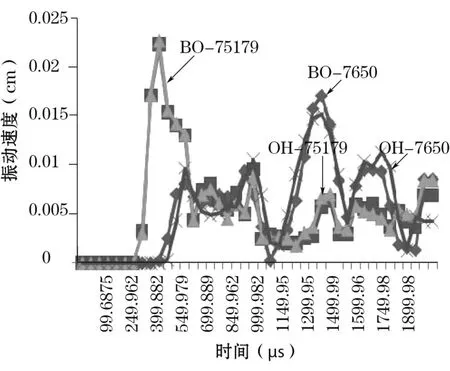
图9 振动速度时程曲线

(7)合成位移。从图10中可看出,60625和75179两点的合成位移在装药结构不同的情况下,其曲线主要趋势和走向相同,值的大小也相差不多。

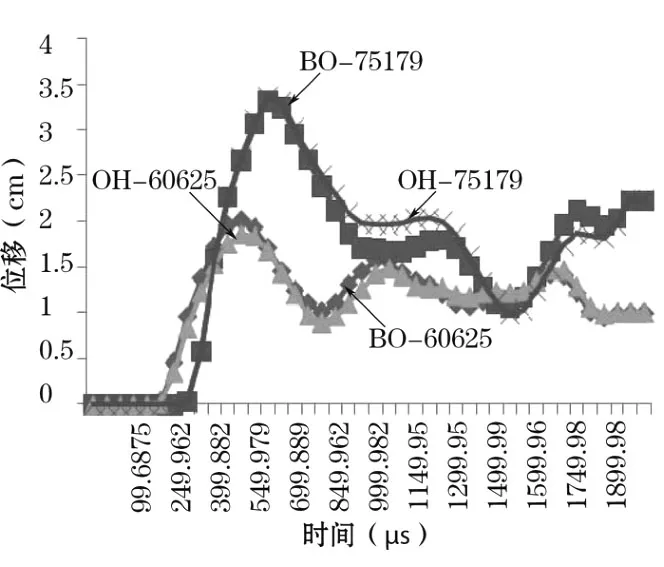
图10 位移时程曲线

2.3 峰值、作用时间长节点比对分析

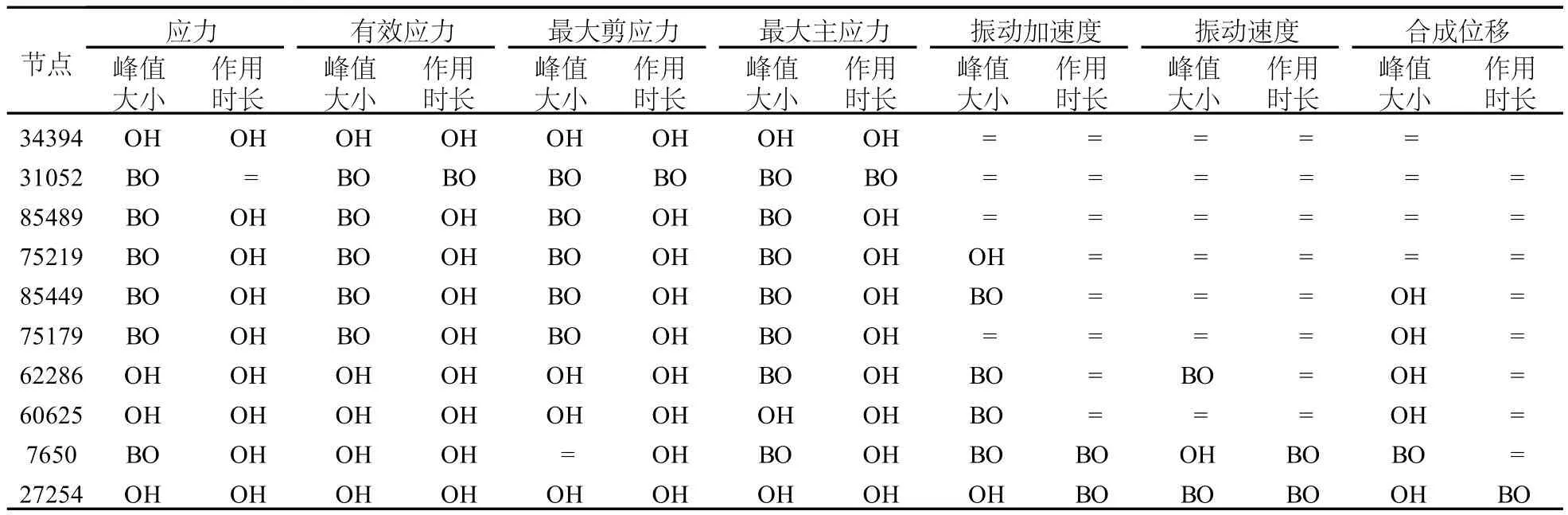
表4 峰值大小、开始作用时间比对

从表4中可以看出,应力、最大主应力在 2种不同的装药方式下,峰值大小有着相同的规律:峰值大小总体表现为模型底部 200 cm范围内的监测质点耦合装药的情况下峰值较大,个别质点不耦合装药峰值较大,200 cm以上监测质点表现为不耦合装药的峰值较大。有效应力、最大剪应力也体现出近乎相同的规律:在模型 200 cm以下监测质点耦合装药的峰值均较大,200 cm以上峰值以不耦合装药较大为主。只是在距离装药中心 106.05 cm处的自由面监测点 34394均体现为耦合装药较大。应力、有效应力、最大剪应力、最大主应力其作用时长的共同特点为:除自由面监测点 31052为不耦合装药作用时长较长外,其余的监测点均以耦合装药作用的时长较长。振动加速度、振动速度、合成位移三者的作用时间均为模型底部 1个或 2个监测点不耦合装药结构的作用时间较长,其余的点 2种装药方式作用时长相同;振动加速度的峰值以模型中下部不耦合装药的峰值较大为主,上部相等。振动速度则为模型底部点的峰值较大,中上部点相同。合成位移则是以中下部监测点耦合装药峰值较大,上部点峰值相同。

3 结 论

通过耦合与不耦合 2种装药方式下的模型计算以及分析,得到以下几点结论:

(1)对于应力、有效应力、最大剪应力、最大主应力来说 2种装药方式对比后发现:耦合装药在模型下部峰值较大,中、上部不耦合装药峰值较大;模型中耦合装药结构的作用时长普遍较长。孔底水柱的缓冲作用降低了冲击波的峰值,使能量扩散的范围增大,显示出耦合装药结构模型底部峰值大于不耦合装药的现象,在中上部由于水柱的折射和自由面的叠加作用,使上部监测点的峰值较大。

(2)在模型的底部由于水柱的缓冲作用增长了冲击波作用的时间,使得振动加速度、振动速度、合成位移量变大,有利于裂隙的形成、发展、扩大;也增大了爆轰能量作用的范围,改变了能量做功的效果,有利于改善孔底岩石的破碎效果。

(3)两模型相同位置的质点监测曲线从模型下部向上相似度越来越高,到了模型的顶部几乎完全重合,说明了水不耦合的作用对炮孔底部岩石的破碎较为有利,对炮孔上部岩石的破碎并无特殊贡献。轴向不耦合装药有利于克服根底,改善炮孔底部能量的做功效果。

[1] 朱红兵.空气间隔装药爆破机理及应用研究[D].武汉:武汉大学,2006.

[2] 赵金昌,李 义,马步才,等.双介质不耦合装药控制爆破方法[J].煤炭学报,2009,34(12):1637-1642.

[3] 宗 琦,陆鹏举,罗 强.光面爆破空气垫层装药轴向不耦合系数理论研究[J].岩石力学与工程学报,2005,24(5):1047-1051.

[4] 刘柳明,朱传云,李 伟,等.预裂爆破轴向不耦合系数的分析计算[J].华中师范大学学报(自然科学版),2002,36(1):47-49.

[5] 罗 勇,崔晓荣.工程爆破中装药不耦合系数的研究[J].有色金属(矿山部分),2008,60(4):39-43.

[6] 秦明武,蒋玉生,李建军,等.外部接触直列不耦合装药爆破法[J].工程爆破,2002,8(1):13-15.

[7] 杨仁树,姜琳琳,杨国梁,等.不耦合定向断裂爆破试验研究[J].煤炭科学技术,2009,37(11):11-13.

[8] 闫国斌,于亚伦.空气与水介质不耦合装药爆破数值模拟[J].工程爆破,2009,15(4):13-18.

[9] 王永庆,李萍丰.深孔台阶爆破径向不耦合不均匀装药数值模拟研究[J].爆破,2007,24(12):23-29.

[10] 王 伟,李小春,石 露,等.深层岩体松动爆破中不耦合装药效应的探讨[J].岩土力学,2008,29(10):2842-2837.

[11] 张建华,李世禄,王玉杰,等.爆炸扩腔数值模拟及分析[J].武汉科技大学学报(自然科学版),2001,24(2):174-177.

[12] 卢文波,陶振宇.预裂爆破中炮孔压力变化历程的理论分析[J].爆炸与冲击,1994,14(2):140-147.

[13] 李裕春,时党勇,赵 远.ANSYS/LS-DYNA10.0基础理论与工程实践[M].北京:中国水利水电出版社,2006.

[14] 黄刚海.间柱采场深孔爆破落矿采矿工艺关键技术数值模拟研究[D].长沙:中南大学,2010.

[15] 尚晓江,苏建宇.ANSYS/LS-DYNA动力分析方法与工程实例[M].北京:中国水利水电出版社,2006.

[16] 时党勇,李裕民,张胜民.基于 ANSYS/LS-DYNA 8.1进行显示动力分析[M].北京:清华大学出版社,2005.

2011-07-06)

钱立坤(1986-),男,研究生,主要从事采矿工程研究。