隧道爆破中合理微差时间的选择

李 鹏,吕良哲,陈智山,陈 策

(长沙理工大学土木与建筑学院, 湖南长沙 410114)

隧道爆破中合理微差时间的选择

李 鹏,吕良哲,陈智山,陈 策

(长沙理工大学土木与建筑学院, 湖南长沙 410114)

通过结合微差爆破的基本原理以及物理学基本公式,推导出隧道爆破合理微差时间的计算公式,对克服实际工程中炮眼利用率不高以及传统隧道爆破作业时微差时间选择的盲目性,具有一定的指导意义。

隧道爆破;微差爆破;掏槽眼;辅助眼;微差时间

我国一些地方单纯地依靠工程经验盲目设置微差时间,掘进效率较低,具体表现为:微差时间过短,掏槽眼爆破后,经过极短时间第一圈辅助眼立刻爆破,此时掏槽眼中的岩石还来不及抛掷出去,并未形成爆破漏斗,以致无法为后续的辅助眼爆破后的碎石提供足够的补偿空间,掏槽眼的掏槽作用不明显,爆破效果不理想,并且很容易产生“挂门帘”和“留门槛”现象。

本文通过研究隧道爆破过程中岩石破碎及抛掷出去的整个过程,分析计算出每个阶段所需的时间,总结出掏槽眼与第一圈辅助眼的最佳时间间隔。

1 岩石破碎及抛掷过程分析

岩石隧道爆破破坏过程分为 3个阶段[1]。第一阶段为炸药爆炸后冲击波径向压缩阶段。炸药起爆后,产生的高压粉碎了炮孔周围的岩石,形成了压碎圈并即将产生裂隙;第二阶段为裂隙扩展阶段,在压碎圈形成的同时,岩石中的冲击波衰减为压应力波,在应力波作用下,岩石在径向产生压应力和压缩变形,而切向将产生拉应力和拉伸变形。由于岩石抗拉强度仅为抗压强度的 1/10～1/50,当切向拉应力大于岩石抗拉强度时,该处岩石被拉断,形成与压碎圈贯通的径向裂隙,在应力波和爆轰气体共同作用下裂隙扩展至自由面,并使岩块具有初始速度;第三阶段为岩石抛掷阶段,此时将破碎岩块看做一整体,以一定的初速度往外抛出,使爆破区形成一爆破漏斗。

由于隧道爆破只有 1个自由面,所以应充分利用掏槽眼爆破所形成的新自由面,哈努卡耶夫认为,后爆破炮孔以在先爆破孔刚好形成爆破漏斗,且爆岩脱离岩体,形成裂缝宽度B=0.8～1.0 cm时起爆为宜[2]。于是微差时间 T为:

式中,t1为爆破后形成压碎圈时间,即爆破后冲击波传至粉碎圈边缘的时间;t2为岩石裂隙扩展时间,即从压碎圈开始形成有里向外的径向裂隙顺爆破漏斗边缘扩展至自由面的时间;t3为被爆岩块脱离岩体距离 B的时间。

2 岩石破碎及抛掷过程时间计算

2.1 形成压碎圈时间

炸药在爆炸后忽略炸药的传爆时间,冲击波形成的压碎圈半径为[2]:

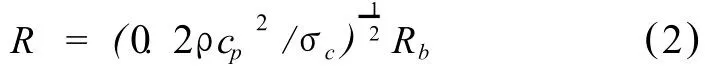
式中:R——压碎区半径(m);

Rb——爆破后形成的空腔半径;

σc——岩石单轴抗压强度;

ρ——为岩石密度,kg/m3;

cp——岩石纵波速度。

爆破后形成的空腔半径为:

式中,r——炮孔半径,mm;

pm——炸药平均爆压,Pa,pm=ρD2/8;

D——炸药爆速;

σ0——多向应力条件下岩石强度,Pa,σ0=

则有:

式中,C为冲击波波速,一般取 3000～5000 m/s。

2.2 岩石裂隙扩展时间

爆破后裂隙沿爆破漏斗破裂半径的方向向外扩展,破裂半径(即裂隙长度)r为:

则:

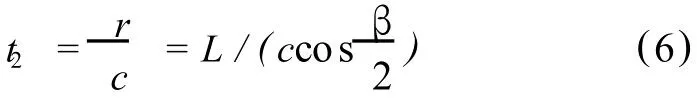
式中,L——炮眼深度;

β——爆破漏斗锥顶角;

c——裂隙平均扩展速度,c=0.1cp[2]。

2.3 被爆岩块离开岩体距离B的时间

该过程为从裂隙刚好贯通至自由面使被爆岩块脱离岩体的瞬间开始至离开岩体距离为 B时结束。掏槽眼爆破装药为耦合装药,在这种情况下,根据声学近似理论[4]可推得岩石炮孔中初始压力 P为:

式中,Pc——爆轰压力,MPa;

ρ0,ρ——分别为炸药和岩石的密度。

则作用在岩石上的平均压力为:

式中,Rb为空腔的半径。

爆破漏斗岩石质量为:

式中,β为爆破漏斗锥顶角。

可以假定,在该过程中被爆岩块始终受到爆轰气体的平均压力的作用,该压力的大小为ηF,η为平均压力损失系数 0＜η ＜1,一般可取为 0.5。则此时取爆岩作为研究对象,爆岩在平均压力的作用下作匀加速运动。根据动量守恒定理,有:

则可得:

综上所述,微差时间 T为:

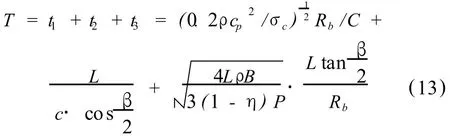
3 工程计算实例

大湾子出口隧道炮眼直径 40 mm,炮眼深度 3 m,最小抵抗线为 0.94 m,岩性为花岗岩(ρ=2600 kg/m3)[3]。Cp=5200 m/s,σc=175 MPa,炮孔半径r=20 mm。炮孔深度 L=3 m,冲击波速度 C=5000 m/s,代入式(2)～式(4),可得 t1=0.4 ms;代入式(5)和式(6),得 t2=8.2 ms;V=250 m/s,代入式(7)～式(10)和式(13),得 t3=22.4 ms。则微差时间 T=0.4+8.2+22.4=31 ms。由于我国目前一般的微差雷管尚无 31ms的间隔时间,可取 50 ms的微差间隔时间,与工程实际间隔时间 50 ms基本相符合,说明此公式是可行的。

分析式(13)可知,选取微差时间关键的是 t3,此时间与炮孔深度和被爆岩块脱离母体的距离有关,炮孔越深,爆破夹制性越大,要求 t3也越长。关于裂缝宽度 B取 0.8～1 cm,有一定的经验性,并且未考虑不同围岩的性质,仅供微差间隔时间选取时参考,也可以说,隧道爆破施工中,微差时间起码要大于或等于 50 ms。

同时式(13)是以掏槽孔为基础推导的,后续炮孔爆破时由于有新的自由面,理论上讲微差间隔时间可以短些,但不宜短于掏槽孔爆破的微差间隔时间,建议后续炮孔还是选微差时间等于 50 ms。

4 结 语

隧道微差爆破的合理时间间隔选择一直是 1个值得深入研究的问题。本文结合普通物理学知识及爆炸力学理论进行推导分析,提出 1个计算微差间隔时间公式,并用工程实践验证了该公式的可行性。当然,将来仍需从更多工程实践着手,通过大量的工程实际数据进行统计分析,完善该公式,从而应用于更多的隧道爆破工程实践。

致谢:本文得到长沙理工大学教学改革研究项目

(JG0849)的资助和吴从师教授的指导,在此表示感谢。

[1] 顾毅成,史雅语,金骥良.工程爆破安全 [M].北京:冶金工业出版社,2001.

[2] 戴 俊,王树仁.爆破工程[M].北京:机械工业出版社,2010.

[3] 王海亮.工程爆破[M].北京:中国铁道出版社,2009.

[4] 戴 俊.柱状装药爆破的岩石压碎圈与裂隙圈计算[J].辽宁工程技术大学学报(自然科学版),2001,(2).

2011-07-06)

李 鹏(1990-),男,湖南岳阳人,隧道与地下工程专业 08级本科生。