基于MANDLEBROT集的分形图形用于丝绸图案设计

蔡燕燕，宋晓霞

(上海工程技术大学 服装学院，上海 201620)

基于MANDLEBROT集的分形图形用于丝绸图案设计

蔡燕燕，宋晓霞

(上海工程技术大学 服装学院，上海 201620)

阐述了复平面上Mandlebrot集的生成方法，设计了基于Matlab相关程序，总结出不同参数下Mandlebrot集分形图形的变化规律，找出了图形结构与函数的基本关系，并运用图像处理软件XFader得到连续图案，在此基础上与法国力克的服装设计软件PrimaVision相结合，将生成的分形图形应用到丝绸图案设计中。

Mandlebrot集；分形图形；丝绸装图案；图案设计

图案设计是丝绸产品开发过程中一个重要的环节，传统的图案设计受到人脑想象力的限制，而且后续的修改过程也比较烦琐，往往成为产品设计中的一个瓶颈。而利用分形的自相似性，再结合计算机，可以在短时间内构造出千变万化而又具有任意高分辨率结构的分形图案。

关于Mandelbrot集的研究已成为人们关注的热点之一。张聿等[1]研究了三角函数Mandelbrot集的图形生成原理，运用计算机绘图方法，并借助电子印花实验，对三角函数Mandelbrot集在印花图案设计中的应用进行了探讨。孙博文等[2]研究了Mandelbrot集在VB、VC++、Java环境下的程序实现。总的来说Mandelbrot集在丝绸图案设计中的应用还较少，且现有的程序设计较为烦琐，不易于被掌握。因此笔者基于Mandelbrot集研究了它的Matlab程序设计，对产生的分形图形的结构特点进行分析总结得出规律，并运用图像处理软件XFader得到连续图案，与法国力克的服装设计软件PrimaVision相结合设计出效果图，将Mandelbrot集产生的分形图形真正应用到丝绸图案的设计中。

1 复平面上的Mandelbrot集

1980年Mandelbrot给世人提供了一幅无与伦比的杰作——Mandelbrot集，如图1所示[3]。

令f(z)＝z2＋c，其中z，c∈C，z是复变量，c是复常数。对变换 f 施行逃逸时间算法，并得到如下所示迭代式：

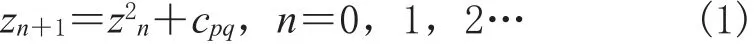
式(1)中：z0＝(0，0)，cpq为计算机荧屏位于(p，q)位置的像素。

因此：

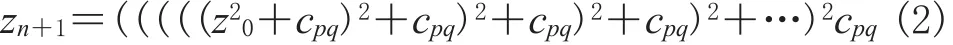
给定N为一个正整数，比如等于255，即画256色彩图。当像素位于(p，q)且n＞N时，复数zn的模数|zn|仍然小于预设的一个阈值k，则在(p，q)位置着色为1，否则当n≤N时，已有|zn|≥k，则在(p，q)位置着色为n(即n数字表示的颜色)，如此(p，q)遍及这个荧屏后，便画出了一幅彩色的Mandelbrot集[4]。

图1 Mandelbrot分形Fig.1 Mandelbrot fractal

2 基于Matlab的程序设计及实验分析

2.1 程序设计

iterations=80;

pixel=500;

p＝linspace(-1.5,1.5,pixel);

q＝linspace(-1.5,1.5,pixel);

[x,y]＝meshgrid(p,q);

c＝x+i*y;

z＝zeros(size(x));

map＝zeros(size(x));

for l＝1:iterations

z＝z.^5 + c;

a＝find(abs(z)>sqrt(5));

map(a)＝l;

end

image(map)

axis off

运行结果见图2，图2为z的5次幂时生成的图形。

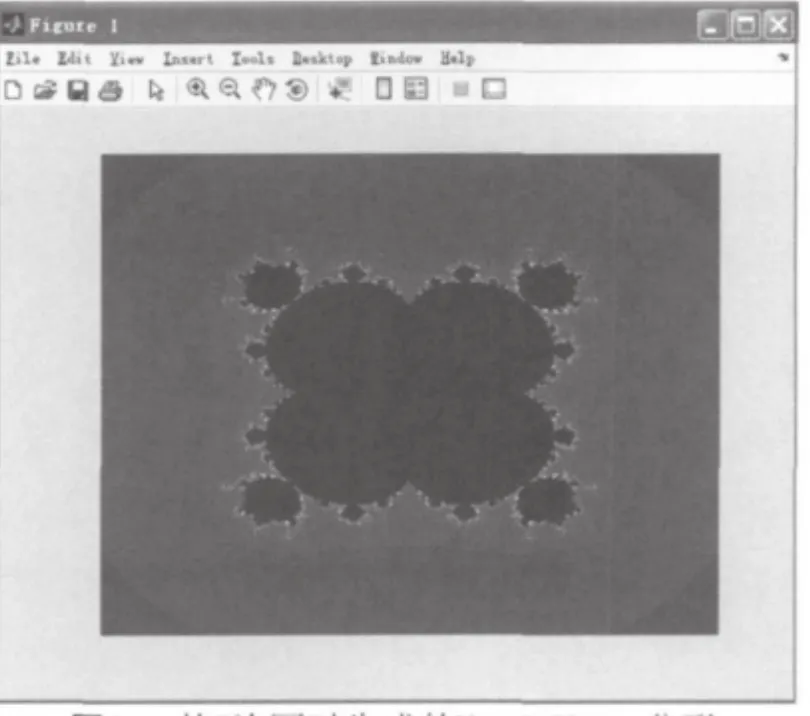
图2 z的5次幂时生成的Mandelbrot分形Fig.2 Mandelbrot fractal when the fi fth power of z

2.2 结果与分析

观察图2，图形的颜色过于单一，不适宜用于丝绸图案的设计，因此对每个数值乘100，以适应所有颜色的变化，否则数值之间靠得太近。生成的图形如图3所示。

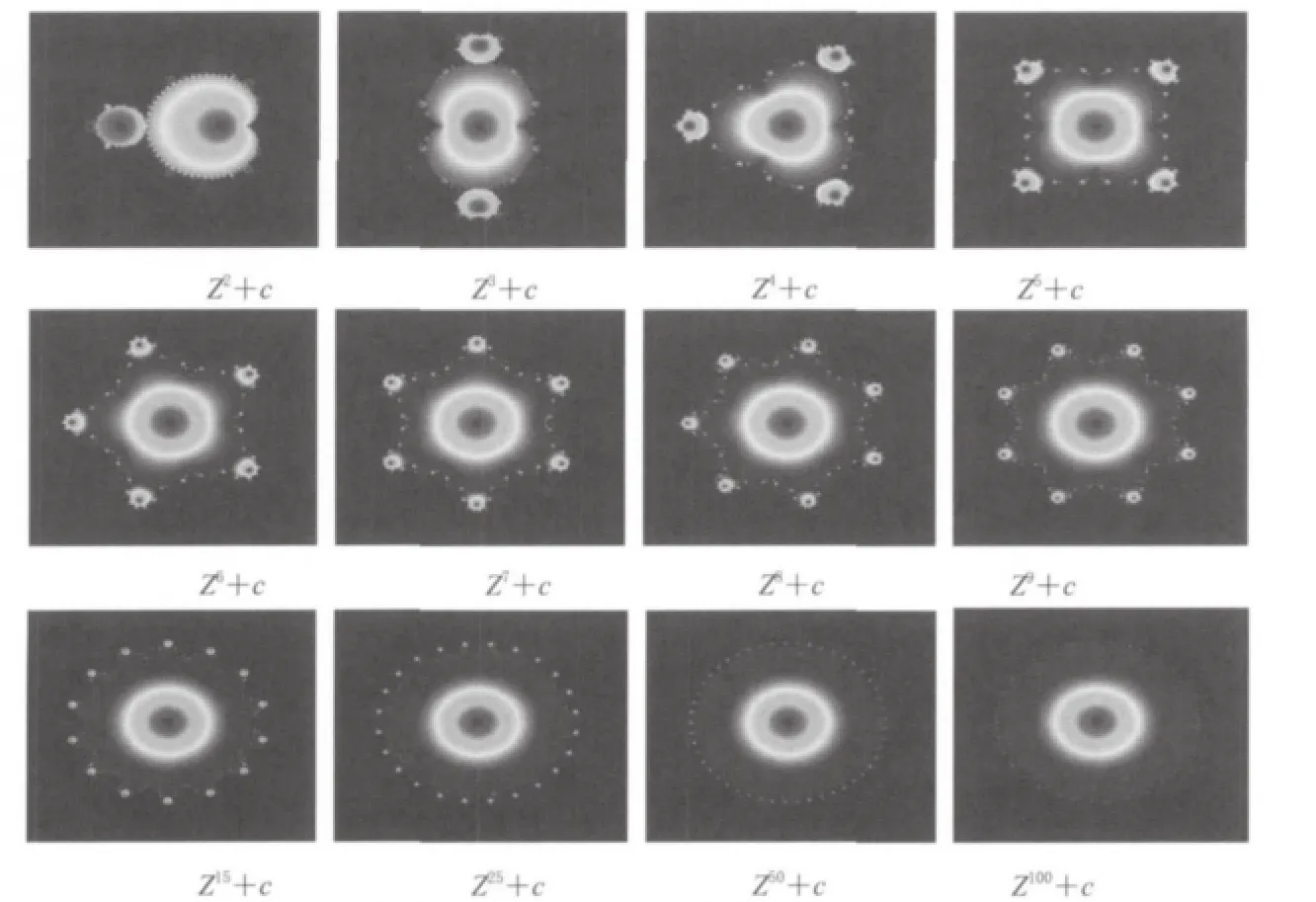
图3 z的次幂取不同值时生成的Mandelbrot分形Fig.3 Mandelbrot fractals when give z different power

从图3可以看出，Mandelbrot分形多为花瓣状，且花瓣数目取决于迭代函数的次幂m，即m阶迭代函数绘制出来的分形图形为m-1个花瓣；图形的外表轮廓大致相似，当m为偶数时，生成的图形关于x轴对称，当m为奇数时，生成的图形关于原点对称；随着m的不断增大，图形的外轮廓越来越趋近于圆。

3 丝绸图案设计

3.1 分形图形的无缝拼接

由于分形图形大多为单独纹样，且具有结构精细、颜色绚丽等特点，一般无法直接运用到丝绸图案设计中，需进行二次设计，例如在分形图形的基础上生成一些二方连续纹样、四方连续纹样等，且图案的结构不能过于精细，颜色数也不宜太多。上文用Matlab生成的分形图形即是单独纹样，无法在丝绸图案设计中广泛应用，因此选取m＝5和m＝7时的分形图制成四方连续图案，在此选用图像处理软件XFader[6]，单击工具栏里的渐变按钮，启用水平与渐变复选框，并将调节滑杆向左移动，就能将图形的边界逐渐融合起来，形成连续图案，在整个过程中，还可对图形的亮度、色调等进行调整。图4与图5是经XFader软件无缝拼接后的图形。

图4 x和y分别位于65 %时的图形Fig.4 The pattern when x and y are located in 65 %

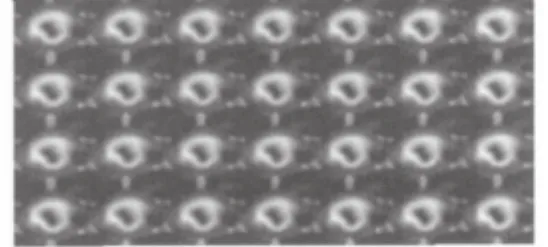
图5 x和y分别位于80 %时的图形Fig.5 The pattern when x and y are located in 80 %

3.2 效果图设计

通过服装设计软件PrimaVision将设计得到的分形图形应用到丝绸图案中。在PrimaVision中，首先利用矢量层次的工具完成款式图的绘制，并将其转换到位图模式，然后利用填色中的图案填入指令完成图案的填入。在填入图案的过程中，为了满足不同效果，可将图案首先进行旋转再填入。图6是经PrimaVision处理后得到的效果图，对填入的图案进行了30°的旋转。

图6 经PrimaVision处理后得到的效果Fig.6 The clothing renderings after the treatment of PrimaVision

4 结 语

通过Matlab设计的基于Mandlebrot集的程序较为简洁。当迭代函数的次数改变时，生成的Mandelbrot集的分形图形的形状也随之改变，分形图形呈现出的花瓣数目取决于迭代函数的次幂m。运用图像处理软件XFader对得到的分形图形进行无缝拼接，得到连续图案。在此基础上与法国力克的服装设计软件PrimaVision相结合设计出效果图，可更直观地展示整体效果。设计过程中，可以根据丝绸面料的加工工艺或织物的组织特点来选择不同的花型图案进行二次处理，个性化地改变图案的色调、亮度等，以满足不同的设计需求。

[1]张聿，付岳莹.基于三角函数Mandelbrot集的印花图案设计初探[J].丝绸，2005(1)：13，51.

[2]孙博文.分形算法与程序设计——VB实现[M].北京：科学出版社，2004.

[3]李水根，赵翔鹏.二维和高维空间的分形图形艺术[M].北京：科学出版社，2009.

[4]徐向红.分形理论在服饰图案设计中的应用基础研究[D].吉林：吉林大学，2009.

[5]秦襄培.Matlab图像处理与界面编程宝典[M].北京：电子工业出版社，2009：414-416.

[6]陈有卿.分形艺术与服装面料图案设计[J].纺织学报，2003，24(3)：88-89.

Application of fractal graphs in silk pattern design based on Mandelbrot set

CAI Yan-yan, SONG Xiao-xia

(College of Fashion, Shanghai University of Engineering Science, Shanghai 201620, China)

This paper described the generation method of Mandelbrot set, and designed the programs based on Matlab. Then, the variation about the fractal graphs of Mandelbrot set in different parameters is studied, the relationships between basic pattern and function are founded. Then the image processing software XFader is used to get some continuous patterns, and the renderings are given after the treatment of clothing design software PrimaVision, applications of fractals in silk pattern design are discussed lastly.

Mandelbrot set; Fractal graph; Silk pattern; Pattern design

TS941.2

B

1001-7003(2011)08-0035-03

2011-03-09；

2011-04-11

蔡燕燕(1986－ )，女，硕士研究生，研究方向为数字化服装技术。通讯作者：宋晓霞，副教授，songxiao xiavivian@126.com。