基于数学概率模型的网络游戏升级问题

白南洋

( 东北石油大学 机械科学与工程学院，黑龙江 大庆 163318 )

0 引言

网络游戏是互联网时代的新型产业之一，具有巨大商业价值.为使游戏在获得利润和增强对玩家吸引力间达到平衡[1]，游戏开发时，游戏策划者需要考虑游戏玩家升级的难度[2].这种难度通常由升级概率表示，难度越高，升级的概率越小.游戏策划者希望了解玩家平均每升级一次的概率，设定游戏规则以平衡游戏的难度[3]，与游戏相关的概率问题引发对“打靶”等问题的研究[4-6].概率论、组合论中的许多理论来源于游戏[7-10]，这些游戏通常包含一些不易解答的问题，如关于“玛丽莲问题”的讨论[11]，以及扑克牌中的概率问题[12]，对它们的研究促进概率学科的建立和发展.分析网络游戏中某类概率问题，即武器装备升级问题，给出该问题的普遍形式并对其中不同情况加以分析，以帮助游戏策划者进行相应的游戏数值策划.

1 恒定概率升级模型

1.1 模型设定

游戏升级规则为：游戏可分级，每次升级通过武器升级实现，武器级别由所拥有的星数标志.假设由m星升级至m+1星成功的概率为p(定值)，不成功则降至1星.求从1星开始成功升级至k星所需要的平均步数.

1.2 分析与求解

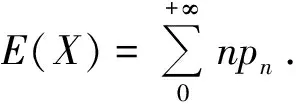
pk-1=p(X=k-1)=pk-1.

由于失败即回到1星，要成功升级至k星，k-1步必为由1星成功升级k星，最后第k步必为升级失败退至1星，且后k-1步一直升级成功.设x1n为经过n步升级至k星，最后第k步为由1星开始升级的概率总和；x2n为经过n步升级至k星，最后第k步为由2星开始升级的概率总和；依此类推，x(k-1)n为经过n步升级至k星，最后第k步为由k-1星开始升级的概率总和，即

pn=x1n+x2n+x3n+…+x(k-1)n.

n+1步升级至k星的情况相当于把n步升级至k星情况中的最后第k步分割为2步，即多插入1步，且最后第k步由1星开始升级，中间可插入1星或2星(插入1星时2步失败，插入2星时先成功后失败退回至1星)；若第k步由2星开始升级，中间可插入1星或3星；依此类推，第k步由k-2星开始升级，中间可以插入1星或k-1星；最后第k步由k-1星开始升级，中间仅能插入1星(此时只能失败，如果成功，就不需要后边的第k-1步).即：无论最后第k步由第几颗星开始升级，中间都可插入1星，此时将1次失败分割成2次失败，在原有基础上再乘(1-p).插入其他星时，如3星升级失败退至1星，插入1个4星，变为3星成功升级至4星，之后升级失败退回至1星，即在原基础上多1次成功升级，需再乘1个p，即

pn+1=(1-p)pn+px1n+px2n+…+px(k-2)n;

同理

pn+2=(1-p)pn+1+p(1-p)pn+…+p2x(k-3)n;

得出

pn+k-1=(1-p)pn+k-2+(1-p)ppn+k-3+…+(1-p)pk-2pn.

(1)

为了给出X的概率分布，给予证明.

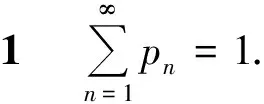
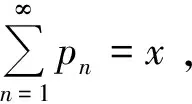
由于p1,p2,p3,…,pk-2=0;pk-1=pk-1,有

x-pk-1=(1-p)x+(1-p)px+…+(1-p)pk-2x，即

游戏策划者关注的重点是升级需要的平均步数，即X的数学期望E(X)，给予证明.

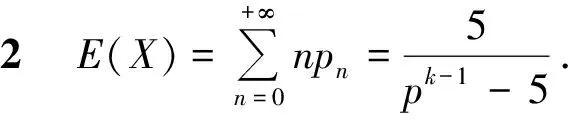
y-(k-1)pk-1-(k-1)(1-pk-1)=(1-p)y-(1-p)(k-2)+

(1-p)py-(1-p)p(k-3)+…+(1-p)pk-2y,

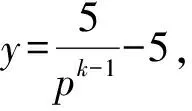
(2)

式(2)即为恒定概率升级模型的升级平均步数计算公式.

1.3 模型应用

当游戏策划者规定打到某级平均需要E(X)步后，可以求出对应概率.如若要求成功打下10星所需平均步数为40，则p≈0.783 38，可以将升级成功概率设为0.783 38.

利用式(2)可以求出给定概率时升级至任意星时所需平均步数.如当p=0.8时，成功升级至2星时，E(X)=1.25；成功升级至3星时，E(X)≈2.81；成功升级至4星时，E(X)≈4.77；成功升级至5星时，E(X)≈7.21.因此，依照所求出的数学期望衡量游戏升级总体难度，如果统计出游戏大多数玩家的平均升级次数，可以估算游戏出现的武器最高级数.

2 不恒定概率升级模型

2.1 模型设定

游戏升级规则为：由1星成功升级至2星的概率为p′(定值)，由2星成功升级至3星的概率为p″(定值)，不成功不降星.求由1星开始成功升级至3星平均需要的步数.

2.2 分析与求解

设成功升级至3星需要n步的概率为pn，则

p2=p′p″,

p3=p′p″[(1-p′)+(1-p″)],

p4=p′p″[(1-p′)2+(1-p′)(1-p″)+(1-p″)2],

依此类推，有

(3)

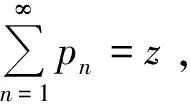
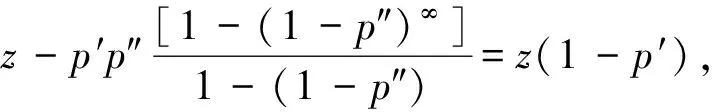
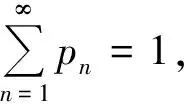
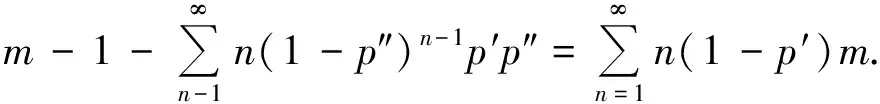
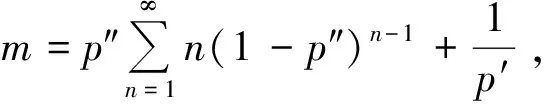
(4)

式(4)即为不恒定概率升级模型的数学期望公式.

2.3 模型应用

将升级至某星的概率代入式(4)，可以求出所需的平均升级步数.如当给定的条件为p′=0.8，p″=0.5时，m=3.25.由此，可以根据需要向上或向下调节不同级别区域内的成功升级概率，达到调控整体难度的目的.

3 结束语

分析网络游戏的概率模型，给出相应模型的概率和数学期望公式，可以依据计算得出的数值进行一定的策划；对于升级概率恒定类模型，可以依照数学期望值衡量整体难度，也可估算游戏中出现武器的最高等级.对于升级概率不恒定类模型，可通过调节不同的升级概率，从而控制难度.