裂隙岩体流动模型综述

王月英， 姚 军， 黄朝琴

( 中国石油大学(华东) 石油工程学院，山东 青岛 266555 )

0 引言

地壳岩石中有许多断层、节理和裂缝，通常将其统称为裂隙[1].根据地质力学，裂隙是失效的结构面[2]，几乎所有的地层中或多或少地存在裂隙[3].在地下流体动力学中，把裂隙发育的岩体称为裂隙岩体，其流动问题是岩石水力学、裂缝性油气藏开发和地下核废料处理等工程领域中的重要研究课题[4-8].流动模拟作为一种工具和手段不仅能够提升对裂隙岩体的认识，同时还能为工程实际管理和决策给予指导[3].流动模拟必须通过流动模型实现，对于某个实际问题，流动模拟是否正确很大程度上取决于流动模型是否合理[4].由于裂隙形态和分布复杂，建立一种适用于所有裂隙岩体的流动模型是不可能的.人们针对裂隙岩体提出多种流动模型，如等效连续介质模型(ECM)、双重介质模型(DPM)、随机连续介质模型(SCM)、离散裂隙网络模型(DFN)、混合模型(HM)以及分形模型等，在确定使用何种流动模型时，必须结合研究域的特点和目的[3-9].笔者对流动模型进行综述，给出模型谱系图，并提出一些新的概念模型.

1 模型综述

裂隙岩体流体流动与传统多孔介质渗流有差别，主要表现为裂隙岩体在不同尺度上的非均质性.模拟裂隙岩体流体流动的主要困难在于描述这种非均质性.人们采用不同的方法技术对这种非均质性进行描述和预测，进而提出多种流动模型，主要包括等效连续介质模型、双重介质模型、随机连续介质模型、离散裂隙网络模型、混合模型和分形模型等.

1.1 等效连续介质模型

等效连续介质模型(Equivalent Continuum Model，ECM)由Snow D[10]提出.该模型是以渗透系数张量为基础，用连续介质方法描述岩体渗流问题的数学模型.Long J C S等[11]、Oda M[12]、张有天[13]、田开铭[14-15]等相继对此模型进行研究.

在ECM模型中，裂隙岩体被看作是一个假想的连续体，系统中每一点的物理量都处于局部平衡状态，重点研究裂隙岩体的宏观流动特征.首先将裂隙中物质参数和裂隙的渗透性等效平均到整个岩体中；再将其视为具有对称张量的各向异性介质，不考虑单个裂隙的物理结构，利用多孔介质渗流理论建立方程.这种等效仅仅是渗流量的等效.

ECM模型的优点是可以利用各向异性连续介质渗流理论进行分析，不需要知道每条裂隙的确切位置和水力特性.对于解决不易获得单个裂隙数据的工程问题是一种很有价值的工具.ECM模型本身并不复杂，该模型的应用存在困难：一是有效性的判定；二是裂隙岩体等效渗透张量的确定.此外，裂隙实际流速一般比等效流速大若干个数量级[1]，因此ECM模型并不适用于非恒定流的分析.

1.2 双重介质模型

双重介质模型(Dual-Porosity Model，DPM)是裂隙岩体流动模拟的常用模型，在石油工业应用非常广泛.DPM模型将裂隙岩体视作等效的连续介质，认为该类介质是由裂隙和基岩两组平行的连续系统组成.其中：裂隙是流体的主要流动通道，其渗透性比多孔基岩的渗透性大得多；多孔基岩是流体的主要储存空间，其孔隙度比裂隙的孔隙度大得多；两套系统遍布于裂隙岩体中，在渗流场的任一点既有基岩又有裂隙，两系统间通过窜流函数联系起来.该模型由Barenblatt G I等[16]提出，Warren J E等[17]对其进一步发展，随后人们对其进行研究并给予不断完善和改进[18-21].目前，双重介质模型分为双孔单渗模型和双孔双渗模型，两者的区别在于后者考虑基岩系统的流体流动过程.

在双重介质的基础上，Abdassah D等[22]提出三重介质模型，以拟合测井数据，将双重介质模型中的基岩系统进一步分为渗流能力和储集能力不同的2类：一类与裂隙联通较好；另一类较差，和裂隙系统构成三重介质系统，其概念思想与双重介质模型没有本质区别.因此，将其与双重介质模型一同综述.

双重介质模型属于另一种连续介质模型，适用于较大尺度的裂隙介质渗流问题.虽然双重介质模型在一定程度上刻画裂隙性介质的优先流现象，并考虑裂隙系统和基岩系统的物质交换，比较符合实际.被裂隙分割的基岩被假定具有相同的大小和形状，过于简化而不能充分表现裂隙介质的各向异性、不连续性等特征；物质交换系数难以确定，尤其是对于两相流或多相流问题尚未有成熟的理论[6，23].另外，与等效连续介质模型类似，在应用时也需要对其有效性进行判定.

1.3 随机连续介质模型

随机连续介质模型(Stochastic Continuum Model，SCM)于20世纪80年代后期由Neuman S P等提出[24]，随后Neuman S P等把SCM模型应用于工程实际[25].他们认为裂隙岩体裂隙的几何条件复杂多变，各种地层参数在空间上是随机分布的，在裂隙岩体空间变异性的影响下，地下流体的流动也具有相应的不确定性和空间分布不规则的特点，故用确定性的方法处理此类问题具有较大的局限性[4，26].在SCM模型中，裂隙岩体被简化为一个基于非参数指标地质统计学的单连续体随机模型，模型参数的统计性质通过现场地质试验获得，岩体的非均质性通过水力传导率参数的强烈变异性表征[3，9].

随机理论方法的实质是把确定性模型中的参数看成具有空间分布的随机场，把随机场离散后代入到控制方程中，研究随机参数的统计特征(一阶矩和二阶矩)和变异性，描述地下流体流动参数的宏观规律性，给出随机参数及随机变量的估值精度和估值区间，以及随机参数和随机变量的波动对流动动态变化的影响程度.SCM模型的关键是其实用性，需要确定研究域的性质是否可以用量测试验尺度得到的参数表征[27-28]，但是随机参数的分布确定比较困难.

1.4 离散裂隙网络模型

为了更精确地描述裂隙岩体的非均质特性，人们用离散裂隙描述方法模拟裂隙岩体中的流动，即离散裂隙网络(Discrete Fracture Network，DFN)模型.DFN模型的研究始于岩石水力学[1,4]，认为基质岩块是不渗透的，地下流体仅在裂隙网络中流动.由此建立单裂隙中的流体流动方程，将所有方程组合在一起求解，从而确定裂隙网络中流体的真实流动状态.DFN模型充分考虑裂隙岩体的非均质性和非连续性特征，能较好地刻画裂隙流体的流动特征.当基质岩块很致密，渗透性可以忽略时，DFN模型具有拟真性好、精度高的优点.目前，二维DFN模型的研究相对比较成熟，三维问题研究尚待深入[9,29].

虽然DFN模型比连续介质模型更接近实际，但仅适用于体积有限、裂隙网络简单且清楚的裂隙岩体流动问题.Louis C等[30]、Wilson C R等[31]、Cacas M C等[32]、Dershowitz W S等[33]对DFN模型进行研究.柴军瑞等[34]、杜广林等[35]对裂隙分级并提出多重裂隙网络模型，将裂隙岩体处理成离散的主干裂隙网络系统、分支裂隙网络系统和概化的等效裂隙网络系统.多重裂隙网络模型既突出主干和分支网络的特殊性，又能反映小裂隙和基质岩块表现出来的连续介质的特性，是DFN模型有效拓展.

在裂缝性油气藏开发中经常遇到具有较大基质孔隙度的裂隙介质，在用离散裂隙网络方法进行流动模拟时必须考虑基岩的渗透性.此时，使用DFN模型不能满足要求，需要在网络模型中考虑较大的基质孔隙度的影响，Noorishad J等[36]提出离散裂隙模型(Discrete-Fracture model，DFM)，随后Baca R等[37]对其进行研究.人们应用DFM模型对裂缝性油气藏中的两相流问题进行研究[38-50].

1.5 混合模型

混合模型(Hybrid Model，HM)是一种基于离散裂隙网络分析的等效连续体近似模型，其基本思想是运用离散裂隙网络方法计算裂隙岩体的等效水力参数，使用连续介质模型预测系统的宏观流动特征.此模型能够结合等效连续体模型和离散裂隙网络模型的优点，在离散裂隙网络模型发展的早期得到体现(Long J C S等)[11].在分析高放核废料场址的渗流时，由于涉及研究域的尺度较大，运用离散裂隙网络方法时计算工作量过大，因此Herber A J[51]、Cacas M C[52]和La Pointe P R等[53]应用混合模型进行研究.

1.6 分形模型

断裂过程导致分形体的出现.裂隙岩体的天然裂隙是与材料的初始脆性相关联的断裂过程所诱导的，因此引入分形理论似乎非常自然.Chang Jincai等[54]第1次将双重介质模型中的裂隙网络看成是分形体系，即将裂隙岩体的导流体系或导流通道看成是分形体系，建立裂隙岩体压力瞬变的分形模型(Fractal Flow Model,FFM).随后Beier R A[55]给出分形模型[54]的推广.Chakrabarty等建立分形油藏单相微可压非牛顿幂率流的径向流模型[56].Acuna J A等应用分形模型[54]分析单井压力瞬态变化[57].Pertamina S A忽略表皮效应和井筒储容的影响，扩展分形模型[58].Dyah R R等用分维数表示双重介质的非均匀性，建立多相径向流的分形模型[59].同登科等使用分形维数和分形指数分别描述裂隙分布状况和裂隙扭曲程度，建立分形油藏非达西低速渗流模型[60].目前，已有的分形油藏渗流模型仅限于对单相流动和流体在双重介质中渗流的情况，尚未有工程应用的相关研究报道[61-62].

2 模型谱系

裂隙岩体流动模型的建立主要是沿着连续介质和离散介质方向开展的.按照连续介质思路建立的模型可以统称为等效连续体模型，包括ECM模型、DPM模型和SCM模型；按照离散介质思路建立的模型统称为离散介质模型，包括离散裂隙网络模型、多重裂隙网络模型、离散裂隙模型等.混合模型可视为两类模型的一种综合应用模型.对于分形模型，均是把分形作为裂隙岩体强烈非均质性的另一种数学描述和工具.

1996年，美国国家科学研究委员会把裂隙岩体中的流动模型划分3种基本类型[3]：(1)等效连续体模型；(2)离散裂隙网络模型；(3)将两种模型联合起来的混合模型.文献[9]也沿用该划分体系.随着对裂隙介质研究的不断深入，简单的谱系划分已不能完全满足需求.笔者对其进行重新划分，见图1.其中，耦合模型(Coupling Model)定义为在研究区域上同时应用2种或多种流动模型耦合而建立起来的.耦合模型能够根据裂隙岩体的实际特征，结合各种模型的优点使之能应用于工程实际，与混合模型存在区别.

耦合模型按耦合方式分为两类：横向耦合和纵向耦合.前者类似于区域分解方法，即把研究区域按照裂隙发育程度和岩体特点分解为多个子区域，在各个子区域上采用不同的流动模型，子区域间通过边界条件予以耦合(见图2(a)).纵向耦合是把2种或多种模型应用于同一研究区域中，模型之间通过物理量之间的显示关系耦合起来(见图2(b)).耦合模型中的一种典型代表见图2，对于某一研究区域也可同时使用2种耦合模型.

连续介质模型的优点是模型简单、理论成熟、容易求解，适合于大尺度流动的研究.当岩体中的裂隙高度离散时，运用连续介质理论分析将产生较大误差，且往往不能充分解释小范围内的量测.此外，在应用连续介质模型时必须对其适用性进行判断.裂隙岩体的一些参数，如裂隙密度、半径、产状和传导性是不能被平均的，这些性质对于岩体中的流动是重要的，是导致裂隙岩体强烈非均质性的主要因素，在建模时必须充分考虑.离散介质模型虽然可以确切地描述岩体裂隙系统的空间结构及其流动特征，但很难直接应用于大规模工程.因此，理论上耦合模型更为符合实际和行之有效，将成为今后的研究重点之一.

图1 裂隙岩体流动模型谱系

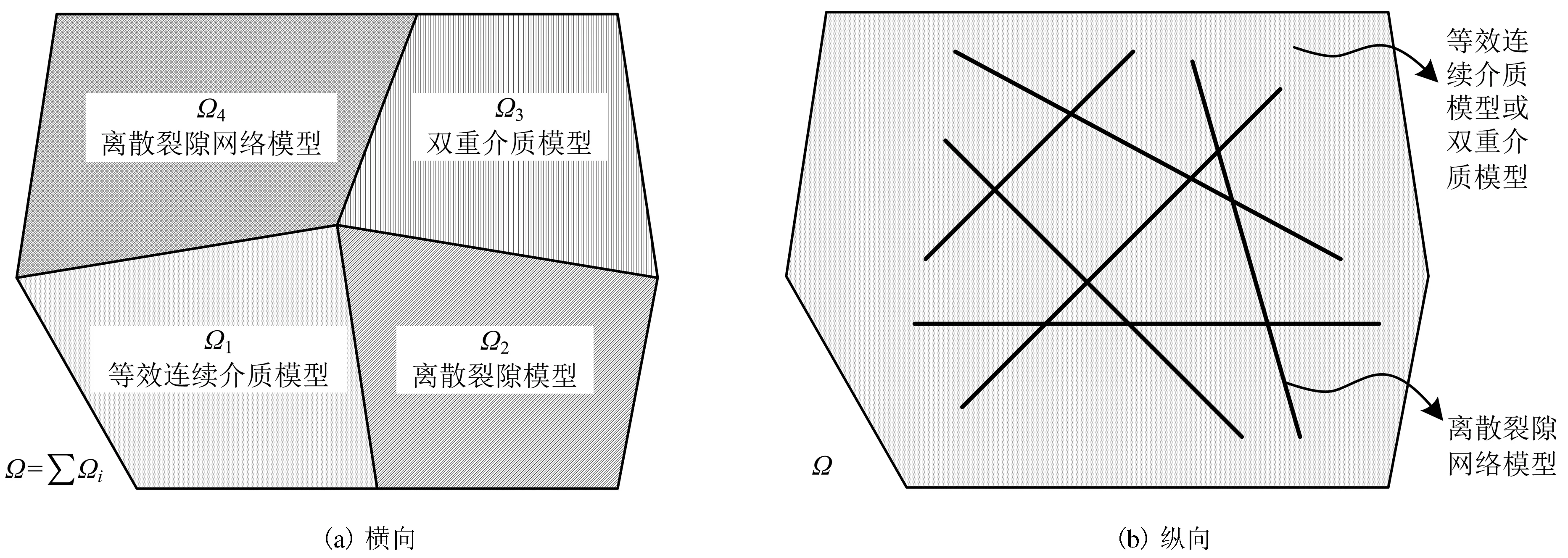
图2 耦合模型示意

3 新型概念模型

基于模型谱系图和耦合模型概念，可以建立一些新的概念模型：

(1)ECM-DFN横向耦合模型.在实际岩体中经常遇到一类介质，在某些区域裂隙发育程度很高，可以很好地等效为ECM模型；在其相邻的区域裂隙发育程度较低，其流动由少数的一些裂隙网络控制，此时应用DFN模型更为合适；对于此类介质，应用ECM-DFN横向耦合模型将更为有效.

(2)DPM-DFN横向耦合模型.与ECM-DFN横向耦合模型不同，该模型在裂隙发育的区域应用DPM模型可以更好地描述裂隙系统的优先流特征，则在裂缝发育区域采用DPM模型，在相邻区域采用DFN模型，采用DPM-DFN横向耦合模型.

(3)ECM -DPM-DFN横向耦合模型.该模型与ECM-DFN和DPM-DFN横向耦合模型没有本质的区别，只是将研究区域划分成3种不同的子区域，并分别应用ECM、DPM和DFN模型.

(4)ECM-DFM纵向耦合模型.类似于DPM模型，把整个研究区域视为2个平行的连续系统：一个连续系统等效为ECM模型；另一个连续系统应用DFM模型进行模拟，系统间通过窜流函数耦合在一起.

(5)SCM-DFN纵向耦合模型.通常研究区域中的宏观主干裂隙网络是确定性的，除此之外采用随机方法描述其非均质性.此时，将研究区域中的主干裂隙网络应用DFN模型描述，而在剩余研究区域应用SCM模型将变得自然和更为符合实际.

在建立耦合模型时将面临关键问题：一是选取和确定流动模型；二是各流动模型之间的耦合关系.对于第1个问题，必须综合现场勘测、测井信息、地震信息等现场数据确定.

图3 流动模型的提出及应用流程

对于横向耦合模型，子区域间需要按照质量、动量和能量守恒引入适当的边界条件；对于纵向耦合模型，需要建立各物理量之间的显示关系.

一个新的概念模型能否作为一个有效的工具指导工程实际，需要解决3个基本问题：(1)该模型能否充分描述研究区域地质特征；如果不能，则需要进行修改或重建.(2)与现有的成熟模型相比，该模型是否具有更好的性能.通过与观测数据的对比进行判定，更为重要的是该模型的预测能力.(3)针对某一研究区域，该模型所需要的模型参数是否足够且容易获得.若不是，则需要确定这些参数及其获取方法.如此不断地反复修正，最终才能成为一种可靠的工具，其修正过程见图3[3].

4 结论

(1)首先对裂隙岩体中现有的流动模型进行综述，总结各种模型的基本原理，对各种模型的优缺点、适用范围进行分析和比较.由于天然裂隙岩体的形态复杂，在确定使用何种流动模型时，应根据研究域的具体特点和研究的目分别对待.

(2)给出裂隙岩体流动模型的谱系图，为选取合理流动模型、求解具体问题提供参考依据.基于耦合模型的概念提出多种新的概念模型——2种或多种流动模型耦合而建立起来的耦合模型，包括横向耦合模型和纵向耦合模型.这些新的概念模型是根据裂隙岩体的实际特点，结合不同流动模型的优点而提出的.

(3)尽管目前裂隙岩体的研究有很大的进展，但也存在一些问题，真正应用于工程实际的流动模型并不多见.在理论上，新的概念模型更趋于实际，具有较好的发展前景.