敞口锚固式储罐壳液耦合有限元分析
王亚轩, 金倬伊, 刘瑞有, 张云峰, 计 静
( 1. 黑龙江八一农垦大学 工程学院,黑龙江 大庆 163319; 2. 黑龙江大学 化学化工与材料学院,黑龙江 哈尔滨 150080; 3. 梧州中国石油昆仑燃气有限公司,广西 梧州 543002; 4. 东北石油大学 土木建筑工程学院,黑龙江 大庆 163318 )
0 引言
储液罐作为石油加工储存的重要设备,其良好的抗震性能是石油工业安全生产的保障[1-4].倘若储罐在发生地震时遭到破坏,将造成严重的经济损失,同时带来如火灾、环境污染等次生灾害[5-7].因此,储罐壳液耦合抗震性能研究具有重要的意义,准确获取储罐壳液耦合的自振特性是开展储罐抗震性能研究的关键[8-9].
孙建刚等[10-14]进行储罐的动力特性分析,考虑储罐与地基的相互作用,采用有限元方法对浮放在地基上的储罐结构进行自振特性计算;周利剑[15-17]采用ADINA有限元软件研究水平地震激励下立式储罐的动力响应,考察储液高度、储罐几何参数和地基刚度对地震响应的影响,同时对比锚固罐和浮罐的地震响应;张艳[18]采用ANSYS软件研究立式圆柱形储罐地震响应,分析不同储液高度情况下的储罐地震效应,模拟使用阶段和施工阶段满罐和空罐工况下的动力分析,结果表明满罐和空罐的底部变形较大,在罕遇地震作用下底部出现“象足”变形;赵晓磊[19]开展15×104m3浮放储罐静、动力数值分析,采用ADINA软件进行模态分析,结果表明有限元与规范计算结果比较接近,储罐液固耦合振动低频的振动形式比较丰富,以cosnθ, sinnθ型梁式振动为主,液体晃动低频的振动形式较单一.
尽管有关储罐的抗震方法和自振特性的研究较多,但应用ANSYS有限元软件[20-21]对储罐壳液耦合自振特性的研究较少,笔者采用ANSYS软件对2 000 m3储罐的壳液耦合自振特性进行仿真分析,得到储罐壳液耦合自振频率和振动规律,并与文献[1]和立式圆筒形钢制焊接油罐设计规范计算结果进行对比,为考虑壳液耦合的储罐抗震分析和设计提供参考.
1 基本周期
GB 50341-2003《立式圆筒形钢制焊接油罐设计规范》[22]采用储罐简化分析模型为Haroun-Housner模型.Haroun-Housner模型假设储液是无旋的、无黏的、不可压缩的介质,将储罐简化成梁模型,认为储罐的cosθ型梁式振动在地震响应中占主要地位,因此采用悬臂剪切梁模型计算储罐的壳液耦合振动固有频率.储罐壳液耦合振动基本周期Tc为
(1)
式中:R为储罐的内半径;δ3为储罐罐壁距底板1/3高度处的有效厚度;Hw为储罐设计的最高液位;Kc为壳液耦合振动周期系数,根据D/Hw(D为油罐的内径)由GB 50341-2003表D.3.2查取.
储罐储液晃动基本周期Tw为
(2)
式中:Ks为晃动周期系数,根据D/Hw由GB 50341-2003表D.3.3查取.
2 计算模型
选取2 000 m3锚固式敞口储罐作为研究对象,罐壁材料为Q235-B碳钢,罐底基础连接形式为锚固型,基本参数见表1.

表1 2 000 m3储罐模型基本参数
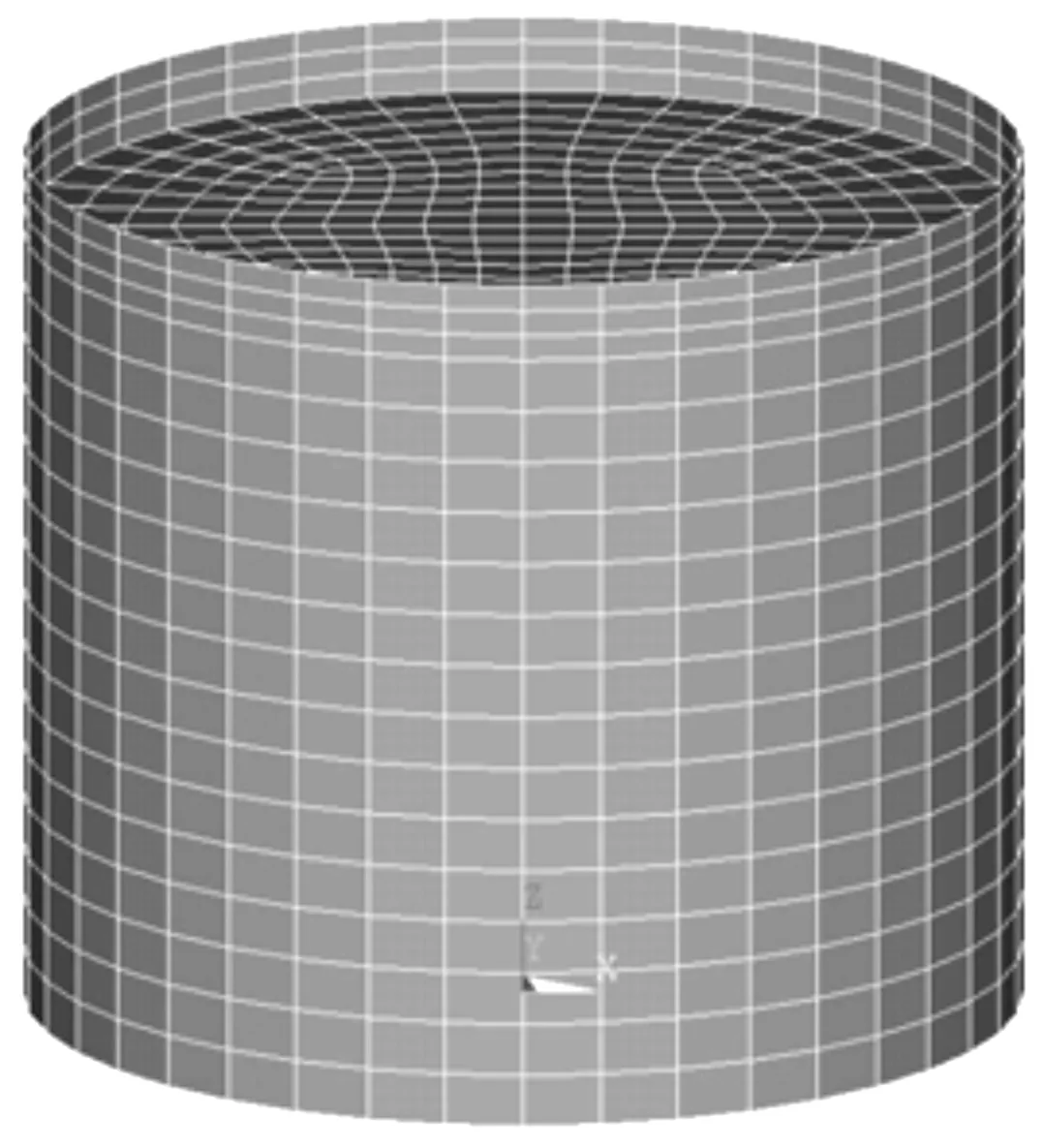
图1 2 000 m3储液罐有限元计算模型
利用ANSYS软件建立储罐有限元计算模型,将罐壁、罐底简化为壳单元[21], 采用SHELL63单元模拟罐壁;采用FLUID80单元模拟储液;采用映射划分单元,沿储液高度划分15网格,沿罐壁圆周划分40网格,得到1 020个壳单元、4 500个储液单元、6 177个节点.划分网格时,为使储液单元和壳单元的节点相互对应,利用ANSYS耦合命令将储液和壳耦合在一起.设置储液自由液面节点的主自由度为储罐高度方向;全部约束罐底单元节点6个自由度,模拟锚固型的基础连接.有限元计算模型见图1,其中:X坐标为水平方向,Y坐标为与X坐标垂直的水平方向,Z方向为储罐的高度方向.
3 模态分析
采用Block Lanczos法进行模态分析,通过扩展模态得到前3阶壳液耦合振动频率和储液晃动频率(见表2).采用文献[1]的方法计算2 000 m3的储罐前3阶壳液耦合振动频率见表2.对比表2计算结果与文献[1]结果,利用ANSYS软件计算的储罐cosθ型梁式振动频率和储液晃动频率与文献[1]结果吻合较好.

表2 2 000 m3储罐壳液耦合振动频率和储液晃动频率 Hz
根据式(1)和式(2)求解得到2 000 m3储罐壳液耦合振动基本周期和储液晃动基本周期分别为0.16,4.00 s,将基本周期换算成基本频率分别为6.250,0.250 Hz(见表2),与ANSYS软件计算的第1阶频率基本吻合,证明所采用的有限元模型和方法可以用于充液储罐模态分析.储罐梁式振动和储液晃动的前3阶振型见图2和图3.
由图2可以看出,2 000 m3储罐的cosθ型梁式振型比较明显,波形突出.在水平地震作用下梁式振动容易被激发,对储罐的抗震性能起主要作用.由表2和图3可以看出,储罐振动的低频阶段为储液自由液面的晃动,储液晃动频率要比壳液耦合振动低很多,属于长周期晃动,频率为0.100~1.000 Hz,因此地震时储液的晃动容易被激发,导致储罐浮顶失效.ANSYS软件计算所得前若干阶频率为自由液面的局部波动,不能作为储液晃动频率;只有自由液面为整体晃动时,才可将其确定为储液晃动.
除梁式振动和储液晃动外,储罐还会发生周向cosnθ多波振型(见图4).由图4可以看出,cosnθ振型在圆周方向呈花瓣形,分布较广,该类振型杂乱无章,参与系数也很小,地震时很难被激发,并非储罐的主要动力特性.

图2 储罐壳液耦合振动前3阶振型


图3 储罐储液晃动前3阶振型
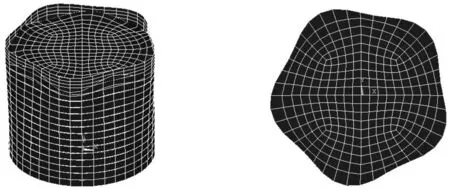
图4 储罐周向cos nθ多波振型
4 结论
(1)利用ANSYS有限元软件,对2 000 m3敞口锚固式储罐进行计算,得到储罐的振动特性,其中:储罐前3阶cosθ型梁式振动频率为6.087,12.748,21.770 Hz,前3阶储液晃动频率为0.247,0.418,0.517 Hz,基本频率与文献和规范计算结果吻合较好.
(2)储罐振动频率为0.100 0~1.000 Hz时,包含自由液面的局部波动和储液晃动,自由液面的局部波动发生在储液晃动前;当振动频率大于1.000 Hz时,为壳液耦合振动,壳液耦合振动包含cosθ型梁式振动和周向cosnθ多波振动.
(3)储罐的cosθ型梁式振型在水平地震作用下容易被激发,对储罐的抗震性能起主要作用.储液的长周期晃动将导致储罐浮顶失效.周向cosnθ多波振型在地震时很难被激发,并非储罐的主要动力特性.

