基于组合赋权TOPSIS模型的项目评标方法研究

□杨宝臣 陈 跃 [天津大学 天津 300072]

基于组合赋权TOPSIS模型的项目评标方法研究

□杨宝臣 陈 跃 [天津大学 天津 300072]

项目评标对业主选择最为适宜的承包商从而确保工程顺利完成至关重要，其本质是多目标情景下对多方案进行全面、客观的评定与优选。为改善现行评标模型的可靠性与便利性，将TOPSIS模型引入到项目评标决策中；通过深入分析评标指标赋权的特殊意义，提出了Delphi-AHP法和熵权法相集成的主客观组合赋权法，使权重既反映决策者主观偏好，又凸显方案客观差异；进而，构建了基于组合赋权TOPSIS模型的项目评标方法。通过案例研究，表明该方法的可行与高效，其得到的评标结果具有更好的区分度与决策精度，可以为业主决策提供更为科学、客观的依据。

组合赋权；TOPSIS；评标；熵权；层次分析法

引 言

近年来，项目招投标制在我国各类工程尤其是大型水利水电、矿产开发、石化建设中得到了广泛应用，既有利于业主选择出符合自身要求的各类承包商，进而确保工程如期、经济、高质量地完成；也使得真正有实力、重信誉的工程单位能够脱颖而出，优胜劣汰，进而有利于相关行业的长期健康发展。在这一过程中，科学、合理、高效地评标，无论对业主、对承包商乃至整个行业而言，都至关重要；其应本着公开、公平、公正的原则，在最大程度满足招标文件实质性要求的前提下，对各投标方案的报价、工期、质量、管理水平等予以全面、客观的评定，进而给出各投标方案优劣次序，为业主选择最优承包商提供科学依据。

目前国内工程建设实务中应用较多的评标方法主要有合理低价法和综合评分法。前者对通过资格预审的方案，单纯比较其投标报价这一个因素，不能全面考量各投标单位在技术水平、项目管理、相关资质等方面的差异，且由于工程成本价或最低合理价往往难以确定，容易发生投标人以低于成本价抢标的不公正事件；而综合评分法尽管通过指标体系和评分标准设计，能够较为全面地评估各投标方案包括报价、工期、质量、组织管理等方面信息，但不能排除专家打分时的个人倾向，主观随意性较强，进而影响评标的公平与公正。所以，尽管这两种方法在评标实务中应用广泛，但存在种种缺陷。对此，有关学者先后提出了层次分析评标法[1]、模糊综合评标法[2-4]、灰色关联评标法[5,6]等一系列方法，它们在一定程度上提高了评标的科学性。然而，这些方法中：层次分析评标法仍然完全依赖于专家经验判断；模糊综合评标法在确定指标隶属函数时往往将很多已是“白化”的信息模糊化处理，进而造成评价误差；灰色关联评标法中，确定关联系数的参数需人为给定，且计算较为复杂；最后，不管是模糊综合评标还是灰色关联评标，目前指标权重的确定大多采用AHP法，单纯考虑主观偏好而忽略评标的竞争性择优属性，且具有很大随意性。

为弥补现有方法的上述缺陷，进一步改善评标的科学性与可靠性，提高评标模型的便利与可推广性，论文将TOPSIS模型引入到项目评标决策中。通过深入研究评标指标赋权的特殊意义，提出Delphi-AHP法和熵权法相集成的主客观组合赋权法，对传统TOPSIS模型进行改进，构建了基于组合赋权TOPSIS模型的项目评标方法；通过案例研究，证明了该方法的可行、高效与便捷。

一、基于组合赋权TOPSIS模型的项目评标方法构建

TOPSIS（Technique for order preference by similarity to ideal solution）模型是经典的多目标决策方法，具有分析原理直观、计算简便、样本量要求不大的特点。其基本思想是首先构造多目标决策问题的理想解和负理想解，通过计算各可行方案与理想解和负理想解之间的欧氏距离，得出不同方案与正负理想解的接近程度，作为方案排序的决策准则；其中，与理想解最近且与负理想解最远的方案，便是方案集中的满意解。在该模型中，理想解是各指标属性均达到最满意的解，而负理想解则为各指标属性均达到最不满意的解[7,8]。

工程评标决策其实质即为一个多目标决策问题，这为TOPSIS模型在项目评标中的应用奠定了良好的基础。同时，考虑到评标体系内不同指标对评标决策具有不同的影响效力和重要程度，理应科学、合理地赋予相应权重，并将其引入到传统TOPSIS模型中，构建基于组合赋权技术的TOPSIS模型，方可为投标决策提供科学依据与有效支持。最后，由于不同行业、不同类型的项目在招标过程中其业主考量重点各不相同，使得所构建的综合评标指标体系不可能做到完全统一，应具体项目具体分析，对此已有大量研究[1,2,9,10]；而本文试图为项目评标决策构建一个一般化的方法，评标指标体系的设计不属于本文探讨的主要内容，对其予以略去。下面具体介绍评标方法的实施步骤。

（一）构造项目评标决策矩阵

设某项目招投标中，有m家单位通过资格预审，评标指标体系中共有n个指标，xij表示第i个投标单位的第j项指标值，同时将(xi1, xi2,…, xin)和(x1j, x2j,…,xmj)T分别记为Ai和Bj(i=1,2,…,m; j=1,2,…,n)，分别表示评标方案属性值和评标指标属性值，则可构造项目评标决策矩阵X：

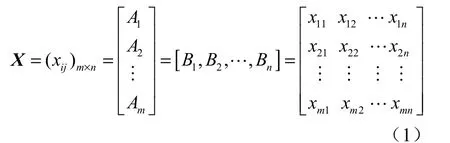
对评标指标而言，一般分为定量指标（如报价、工期、主材用量等）和定性指标（如施工技术水平、质量控制能力、项目管理水平等）两类。对前者，直接选取投标单位或方案的定量数值作为xij的取值；对后者，则应进行量化处理，根据需要选取专家直接评分、模糊综合评分、量表评分[11,12]等方法确定xij数值。

（二）数据同向无量纲化处理

为消除各指标由于量纲、数量级和对评标目标影响方向的不同而可能造成的决策失误，需要对决策矩阵X进行同向无量纲化处理，构造标准化决策矩阵 Y=(yij)m×n；为降低TOPSIS模型计算的复杂度，这里采用极差法处理。

对效益型指标：

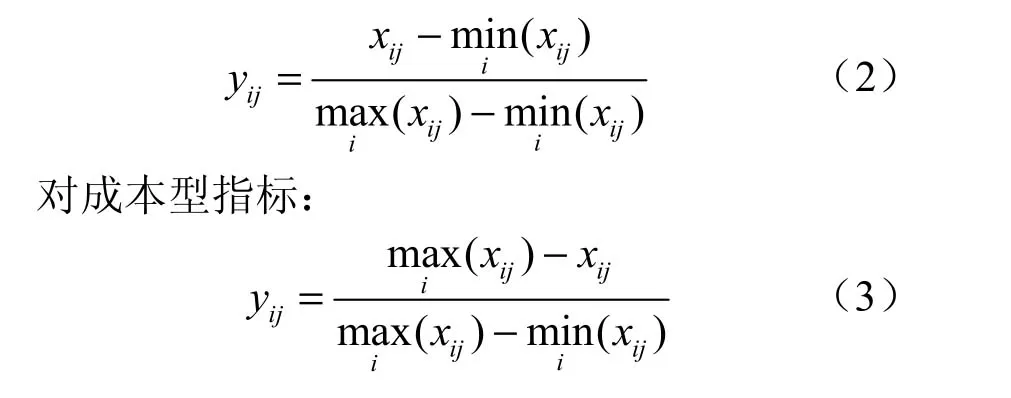
（三）指标的主客观组合赋权

在多目标决策模型中，指标权重设定的合理准确与否将会对决策结果产生很大影响，应根据决策问题的具体特点科学选择赋权方法。项目评标决策既应恰当反映招标方决策者或评标专家的主观偏好，又应建立在对各投标方案客观、公正地择优比选基础上。具体到评标指标赋权问题上，就是既应体现决策者或专家对评标指标的不同要求、关切或重视程度，又应凸现出各投标方案之间的竞争程度或差异性，比较客观地做出择优决策；最终兼顾主观偏好与客观信息，得到比较合理可靠的指标权重。举例来说：对某一工程，若招标单位对其报价尤为看重的话，则较之其余指标“报价”指标理应赋予较大权重；另一方面，若实际各方案在具体报价上相差不大，则“报价”指标对选择最优投标方案提供的信息较少或帮助不大，从这个意义上而言，其又应赋予较小的权重；最后的权重应是对这两个方面的综合考量与平衡。这便是评标决策中指标赋权的特殊意义所在，也是本文采用Delphi-AHP法和熵权法相集成的主客观组合赋权法的基本思想。因Delphi-AHP法在相关文献中讨论较多，以下仅介绍熵权法和组合赋权技术的具体算法。

1．熵权法算法

熵（Entropy）是信息论中测度系统不确定性或无序化程度的量，其值越小，不确定性越小，所含信息量越大，反之亦然。熵权法就是根据各指标值所提供客观信息量的大小来确定指标权重的方法。其基本思想是：在上述标准化决策矩阵 Y=(yij)m×n中，对给定的第j项指标，yij(i=1,2,…,m; j=1,2,…,n)的差异越大，表明该指标对评标方案的比较作用越大，也即该项指标包含和传输的信息越多，则其熵值越小，熵权越大，具体步骤如下[13]：

（1）计算第j项指标的熵值ej：

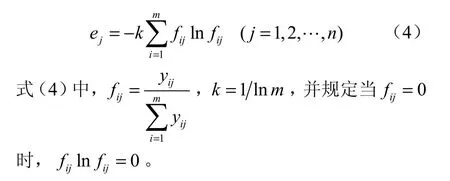
（2）计算第j项指标的差异系数gj：

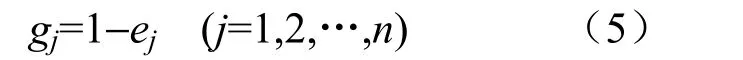
（3）计算第j项指标的熵权jβ：

2．组合赋权法

设由Delphi-AHP法得到的指标主观权重向量为α=(α1,… ,αj,… ,αn)，而由指标熵值得到的客观权重向量为 β=(β1,… ,βj,… ,βn)。组合赋权法就是将二者进行综合集成，使最终的指标权重既反映主观经验判断与决策偏好，又反映客观评标信息与方案差异；就处理方式而言，通常有加法组合法与乘法组合法两种。考虑到项目评标指标往往较多，权重一般相差不大，为尽量凸现指标间重要性差异，本文选取乘法组合赋权法，则最终指标权重ωj为：

（四）构造加权标准化决策矩阵

将以上得到的主客观组合权重向量ω=(ω1,… ,ωj, … ,ωn)引入到决策矩阵中，构造加权标准化矩阵Z：

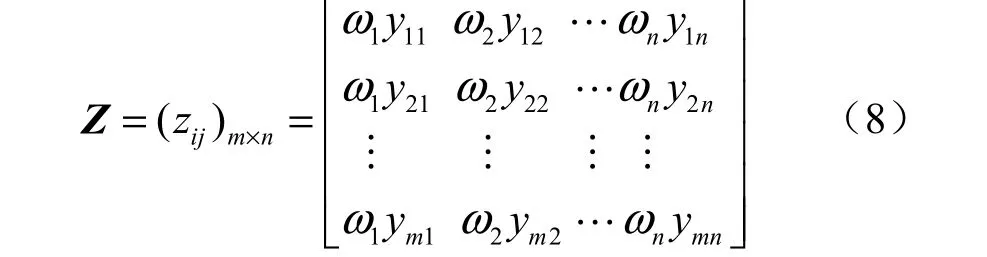
（五）确定理想解与负理想解

依照TOPSIS模型算法要求结合指标的不同类型，按下式分别确定正理想解Z+和负理想解Z-：

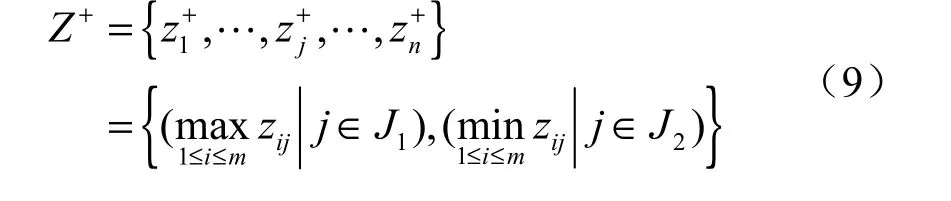
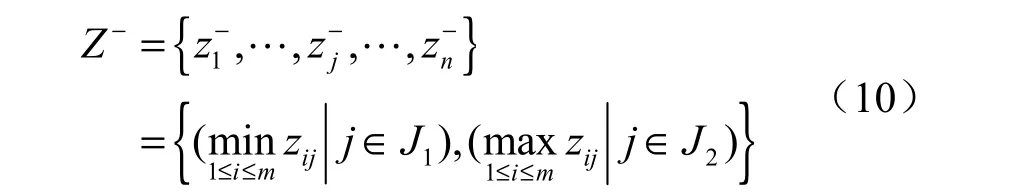
以上二式中，J1为效益型指标集，J2为成本型指标集。

由于前面采用了极差法进行指标的同向无量纲化处理，得出本论文构建的基于组合赋权TOPSIS模型的项目评标方法下，正、负理想解分别为：

这在一定程度上使模型的计算更为简易、可行。

（六）计算欧氏距离

各投标方案与正、负理想解间的距离分别为：

（七）计算相对贴近度并排序

各投标方案与理想解的相对贴近度Ci为：

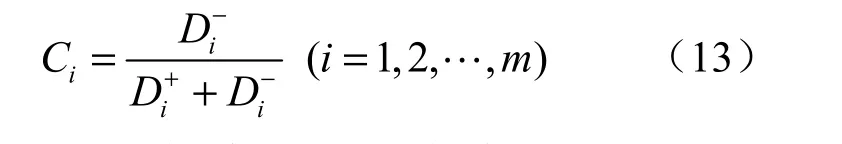
Ci越大，方案越优；反之亦然。对所有Ci(i=1,2,…,m)进行排序便可确定最优投标方案，进而为业主的评标决策提供支持。

二、应用实例

（一）实例概述

为更好地说明所提出的基于组合赋权TOPSIS模型的项目评标方法的效果，本文采用文献[6]中的某建筑工程投标商选择案例进行实证分析。该案例选取工程报价、工期、企业财务状况、施工经验、施工组织设计、质量保证体系、项目经理业绩这七个指标构成评标指标体系；对前四个指标直接采用投标书或有关证明材料上的相关数据（报价货币值、承诺工期天数、企业注册资金、已建或在建类似工程面积），而对后三个指标则通过专家百分制打分完成定性指标的定量化处理；指标体系中，除工程报价、工期为成本型指标外，其余指标均为效益型指标；相关评标数据见表1所示。

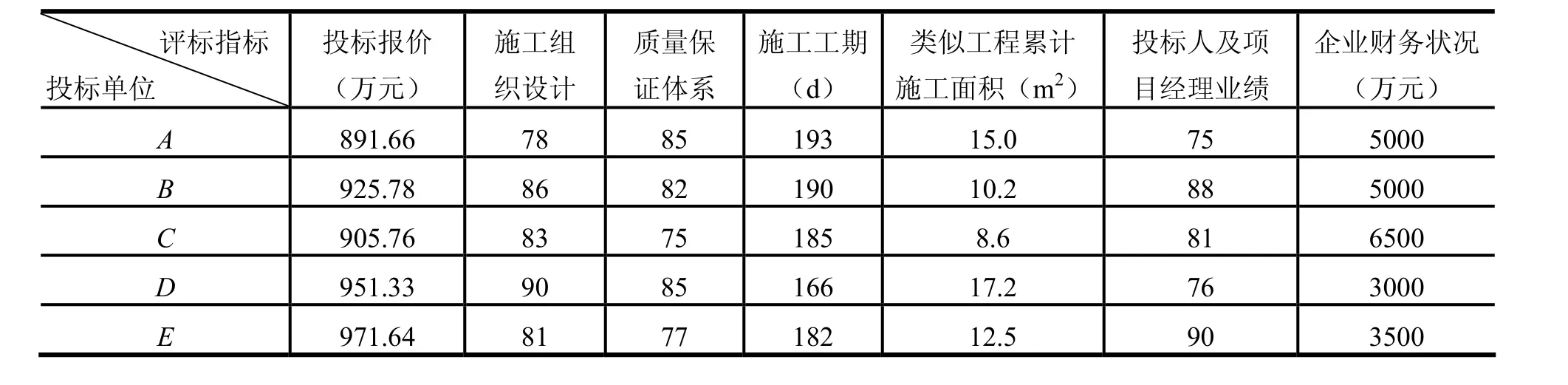
表1 某建筑工程投标单位选择案例数据

（二）计算过程

采用上文构建的基于组合赋权TOPSIS模型的项目评标方法，以Matlab7.0为工具编程运算，对案例中投标单位的优劣进行排序，具体过程如下。

1．构建标准化决策矩阵

表1可直接构成评标决策矩阵X，在此基础上，利用式（2）和（3），进行指标的同向无量纲化处理，构造标准化决策矩阵Y：

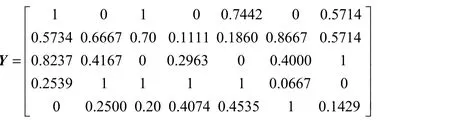
2．求解指标熵权与主客观组合权重

根据式（4）、（5）和（6）计算指标熵值ej、差异系数gj和熵权jβ（j=1,2,…,7)；根据式（7）将熵权法得到的指标的客观权重与主观权重进行集成；这里，评标指标的主观权重直接采用文献[6]中由Delphi-AHP法得到的权重数值；相关数据与计算结果见表2所示。

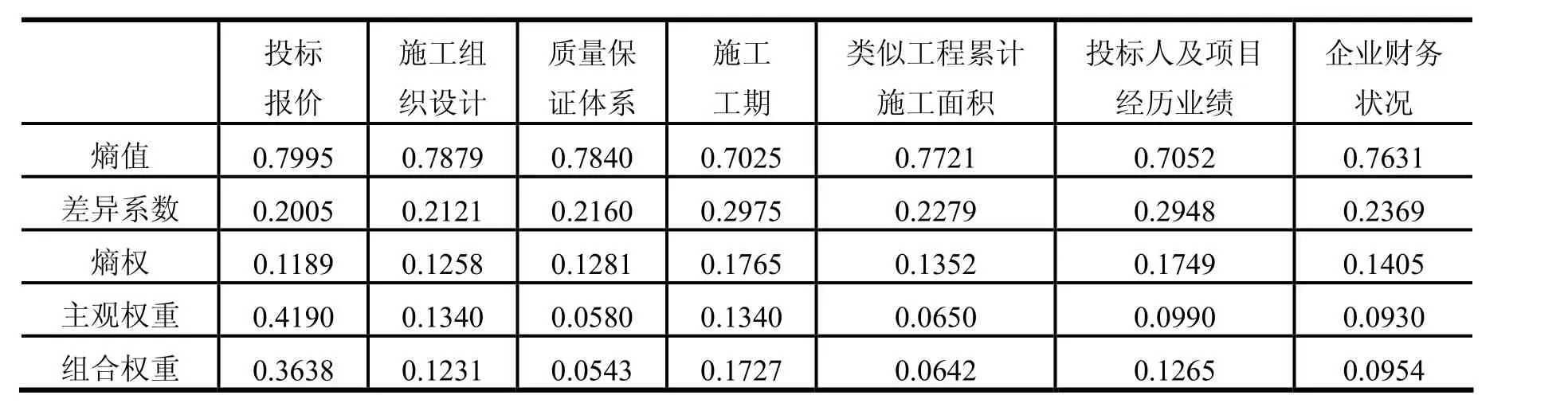
表2 评标指标熵权与组合权重求解过程

3．构造加权标准化决策矩阵

根据式（8）可得：

4．TOPSIS模型计算并排序

由上文分析知，正、负理想解分别为Z+={0.3638，0.1231，0.0543，0.1727，0.0642，0.1265，0.0954}和Z-={0，0，0，0，0，0，0}。根据式（11）、（12）分别计算各投标方案与理想解、负理想解间距离；进而，通过式（13）得到相对贴近度；最后，通过相对贴近度排序做出方案优选决策，即五个投标单位按从优至劣的顺序依次为C、A、B、D、E，C单位方案最优；相关结果见表3所示。

（三）效果分析

表3列示了本文所提出的基于组合赋权TOPSIS模型的项目评标方法应用于案例的有关计算结果，还将文献[6]所提灰色关联评标方法对同案例的评标结果一并列出，方便进行对比研究，不难发现：

1．应用本文方法得到的投标单位排序与文献[6]中的排序完全一致，说明所提方法的可行与准确。

2．从两种评标方法下分别作为方案排序依据的相对贴近度和灰色综合评价值来看，前者在所有投标单位上的极差更大、值域更宽、两两差异更显著，也即本文所提方法能够更好地“拉开”各投标单位的档次。因此，较之灰色关联评标方法，基于组合赋权TOPSIS模型的项目评标方法对于方案优选具有更好的区分度与决策精度。

此外，就方法的实施过程而言，本文所提方法在评标指标权重设定上将专家或决策者的主观偏好与评标客观信息予以有效集成，最大程度地确保了评标决策的适应性和客观、公正性。

三、结语

本文将多目标决策理论中的TOPSIS模型应用于评标过程，通过对项目评标本质特点与特殊要求的深入分析，提出了Delphi-AHP法和熵权法相集成的评标指标主客观组合赋权法，构建了基于组合赋权TOPSIS模型的项目评标方法。该方法实现了评标过程主观与客观、定性与定量信息的有效集成，弥补了现有方法在评标过程与指标权重确定上的主观随意性，最大程度地反映了评标决策要求，有助于提升评标决策的科学性与精确性；此外，该方法不依赖于具体的评标指标体系，且计算简单，易于使用和推广；最后，基于组合赋权技术的TOPSIS模型还可广泛应用于所有涉及方案比较、优选的实际问题。

[1] 侯立中, 吴俊霞. 层次分析法在石油工程评标中的应用[J]. 技术经济, 2006, 25(5): 113-115.

[2] 肖蕾, 王俊和. 基于价值工程的铁路建设工程评标方法探讨[J]. 铁道学报, 2009, 31(1): 111-114.

[3] 吴耀兴, 陈政辉. 模糊综合评价法在工程项目评标中的运用[J]. 建筑经济, 2009, (10): 64-67.

[4] 徐建新, 陈卫宾, 曹玉升, 等. 半结构多目标模糊优选理论在工程评标中的应用[J]. 中国农村水利水电, 2005,(4): 72-75.

[5] 张熠, 王先甲. 一种基于灰色关联和模糊理论的工程项目评标方法[J]. 技术经济, 2009, 28(12): 43-46.

[6] 刘晴, 王建平, 王丛莹. 基于灰色关联理论的建设工程评标方法研究[J]. 工程管理学报, 2010, 24(2): 152-155.

[7] OPRICOVIC S, TZENG G H. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS[J]. European Journal of Operational Research, 2004,156(2): 445-455.

[8] 钱吴永, 党耀国, 熊萍萍, 等. 基于灰色关联定权的TOPSIS法及其应用[J]. 系统工程, 2009, 27(8): 124-126.

[9] 张水波, 张蕾, 高原. 工程总承包模式下的综合评标指标体系研究[J]. 天津大学学报(社会科学版), 2005, 7(2): 97-101.

[10] 潘彬, 张得让. 政府采购招标项目评标方法——基于模糊数学综合评判分析法[J]. 系统工程, 2007, 25(2): 97-100.

[11] 郭亚军, 张发明, 易平涛. 标度选择对综合评价结果的影响及合理性分析[J]. 系统工程与电子技术, 2008,30(7): 1277-1280.

[12] 穆瑞, 张家泰. 基于灰色关联分析的层次综合评价[J]. 系统工程理论与实践, 2008, 28 (10): 125-130.

[13] 周晓光. 基于熵权的模糊物元决策[J]. 系统管理学报, 2009, 18(4): 454-458.

编辑 何 婧

Study on Project Bidding Evaluation Method Based on Combination Weighting TOPSIS

YANG Bao-chen CHEN Yue
(Tianjin University Tianjin 300072 China)

Project bidding evaluation is of vital importance for owners to select the most suitable contractors to complete the project successfully. In order to improve the reliability and convenience of existing methods,TOPSIS model is introduced into project bidding evaluation. Through analyzing the special meanings of weighting for bidding evaluation indexes, this paper proposes a combination weighting method integrating Delphi-AHP and entropy method, which not only reflects decision-makers’ subjective preference but also highlights the objective differences of schemes. Then, the project bidding evaluation method based on combination weighting TOPSIS is established. Finally, a case study is given, which shows the method introduced in this paper is feasible and efficient,and has better differentiation degree and decision accuracy.

combination weighting; TOPSIS; bidding evaluation; entropy weight; AHP

F270

A

1008-8105(2011)01-0050-05

2010 - 09 - 28

“十一五”国家科技支撑计划项目（编号：2006BAB08B01）；天津大学自主创新基金资助项目

杨宝臣（1966 - ）男，教授，博士生导师，天津大学管理学院技术经济研究所所长；陈 跃（1982 - ）男，天津大学管理学院博士研究生.