分数阶微积分及其应用

祝奔石

(黄冈师范学院数学与计算机科学学院，湖北黄州438000)

分数阶微积分及其应用

祝奔石

(黄冈师范学院数学与计算机科学学院，湖北黄州438000)

本文介绍了分数阶微积分的历史、基础知识以及在实际问题中的应用.

分数阶微积分;分数阶Riemann－Liouville导数;分数阶Caputo导数;应用

1 分数阶微积分的历史与基础知识

在展开论述之前，首先介绍一下分数阶微积分的定义.所谓分数阶微分或积分，不是指一个分数或一个分式函数的微积分或微分，而是指微分的阶数和积分的次数不是整数，它可以是任意实数，乃至于复数.当然，就目前而言，在实际问题中还没有出现阶或次数为复数的情形.分数阶微积分的历史几乎和整数阶微积分的历史一样久.1695年，微积分的发明者、德国数学家Leibniz和法国数学家L’Hospital就曾以书信的方式探讨过把整数阶导数扩展到非整数的情况.比如说，令，则对于这个问题，Leibniz也是一头雾水，没有给出一个合理的答案.n(n=124)年后，Lacroix首次给出了这一问题的正确解答:由于分数阶微积分理论与通常的整数阶微积分理论相左，又没有实际应用背景，在此后的一百多年里一直发展缓慢，直到1983年Mandelbort首次指出自然界及许多科学技术领域中存在大量的分数维事实，且在整体与局部之间存在自相似现象以后，作为分形几何和分数维的动力学基础，分数阶微积分才重新获得了新的发展而成为当前国际上的一个热点研究课题，并在许多领域得到了广泛的应用.1974年，在美国纽黑文大学召开了第一届分数阶微积分及其应用国际学术会议，并以Lecture Notes in Mathematics系列丛书形式发表了第一部关于分数阶微积分理论和应用的会议文集［1］.同年，Oldham和Spanier出版了第一部分数阶微积分专著［2］.此后，该领域的研究蓬勃兴起，许多关于分数阶微积分方面的书籍被出版，如文献［3－8］.在美国数学分类号2010版(Mathematics Subject Classification 2010，简称 MSC 2010)中也增加了分数阶微积分的条目.另外，至少有两种关于分数阶微积分的国际杂志Journal of Fractional Calculus和Fractional Calculus and Applied Analysis被公开发行.

为了说明分数阶导数和分数阶积分的定义，我们先来回顾经典微积分中求导运算和求积分运算的关系.定义求导运算D和求积分运算Jα如下:

它们满足关系式

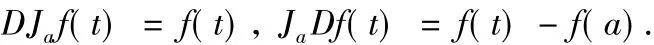
这说明求导运算D是求积分运算Ja的左逆运算，且这两种运算一般来说不具有交换性.进一步，对任何自然数n有

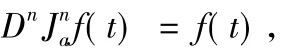
即求导运算Dn是求积分运算Jna的左逆运算.对连续函数f(t)，反复应用分部积分法可得

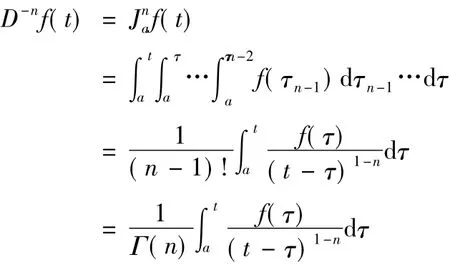
其中Γ(·)是Gamma函数，且Γ(n)=(n－1)!.因此，对非整数的正数α＞0，我们可以定义分数阶积分

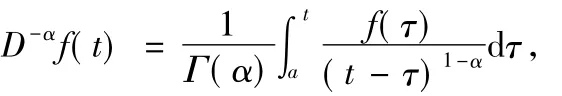
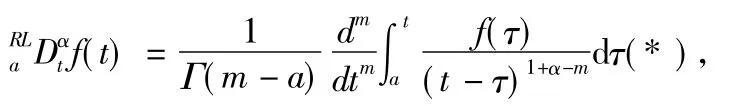
如果利用D=DD，非整数 α阶 Caputo导数定义为

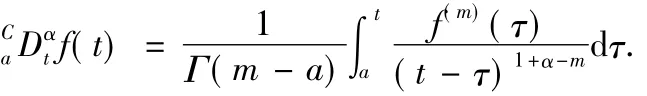
这里应该说明的是，与整数阶导数定义只有一种不同，数学家从不同的角度出发，给出了分数阶导数的多种定义，Riemann－Liouville导数和Caputo导数是其中应用比较广泛的两种.

下面说一下这两类导数的区别.对于非整数α阶Riemann－Liouville导数而言，是先求m－α次积分(相当于－(m－α)阶导数)，再求m阶导数，可大致理解为先积再微，少积多微.而对非整数α阶Caputo导数而言，是先求m阶导数，再求m－α次积分(相当于－(m－α)阶导数)，可理解为先微再积，多微少积.引入Riemann－Liouville导数定义，可以简化分数阶导数的计算;引入Caputo导数定义，让其拉普拉斯变换式更简洁，有利于分数阶微分方程的讨论.

接下来说说这两类导数与整数阶导数的联系和区别.当α=n时，这两类分数阶导数与通常的整数阶导数一致.同样，这两类分数阶导数和整数阶导数一样也有线性性质.另外，对函数f(x)先求α次积分再求α阶导数，它的值仍然是f(x).但是它们之间还是有很大的区别.整数阶导数反映的是函数在某一点的局部性质，而分数阶导数从定义上看实际上是一种积分，它与函数过去的状态有关，反映的是函数的非局部性质.分数阶导数的这种性质使得它非常适合构造具有记忆、遗传等效应的数学模型.我们也可以从卷积的角度来说明分数阶导数与整数阶导数的区别［2］.为简单起见，不妨设a=0.令核函数

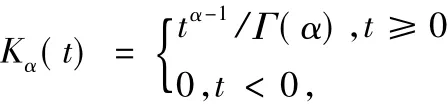
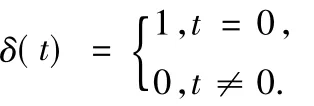
从运算方面看，分数阶导数公式都很复杂，对乘积、商与复合运算没有整数阶导数那样简单的求导公式，计算复杂性大大增加.下面举一个简单的例子说明两者之间的差别.我们知道，常数的正整数阶导数为零，但分数阶导数不一定为零.比如，设f(t)=c≠0，对0＜α＜1，有

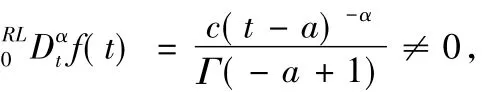
2 分数阶微积分的应用

如前所述，分数阶微积分发展缓慢除了与经典的整数阶微积分不一致之外，也因为它暂时在实际问题中没有得到广泛应用.分数阶微积分的第一个应用是1832年Liouville提出的位势问题方程，第二个应用是1881年A-bel提出的等时降落线问题.在近20年里，它的应用范围逐渐扩大，应用领域涵盖流体力学、流变学、粘弹性力学、分数控制系统与分数控制器、电分析化学、生物系统的电传导、神经的分数模型以及分数回归模型等［8］.

下面给出一些例子来说明分数阶微积分的应用.为了使符号简化，这里把非整数α阶Riemann－Liouville导数简写成

例1粘弹性材料模型［9，10］.力学中，理想弹性材料的弹性力与弹性形变服从胡克定律，即

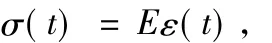
而理想牛顿流体的应力与应变则满足如下方程

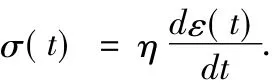
粘弹性材料既不是理想固体，也不是理想流体，而是介于理想固体与理想流体之间，因此，粘弹性材料所满足的模型可表示为

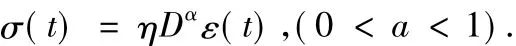
例2PIλDμ控制模型［11］.经典的 PID 控制器的输出方程中，积分和微分都是整数阶的.近年来的重要推广是其中积分的次数和微分的阶数可以是任何实数.其传输函数为

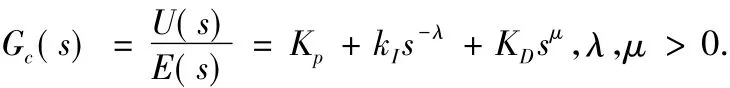
输出函数为

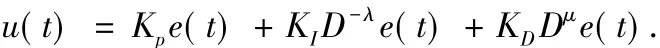
若λ=μ=1时便是经典的PID控制器.若λ=1，μ=0时是控制器，若λ=0，μ=1是PD控制器.

分数阶状态反馈控制比经典状态反馈控制更精确，而且具有很多良好的控制性能，如对增益变化有很好的鲁棒性、能抗高频噪声、易于消去静态误差等等.分数阶控制的应用包括:车辆主动悬架、液压动作器、柔性机械臂、机器人等诸多运动控制问题［12］.

例3广义牛顿定律.我们熟知的牛顿定律的形式是，Westerlund建议把它改为

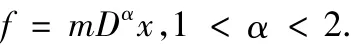
相关的争论可参见文献［13］.

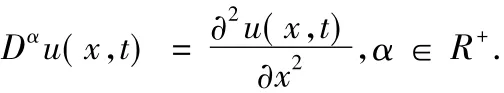
例4扩散波动方程［14］.Nigmatullin的一维扩散波动方程为易知，当α=1时，是抛物型方程，是经典的扩散方程;当α=2时，是双曲型方程，是经典的波动方程.于是Mainardi把它叫做“扩散波动方程”.

例5变分原理是研究保守力学系统的重要方法，利用它所推导出来的方程是整数阶微分方程.对于具有摩擦或其它耗散过程的非保守系统，它不成立.如果将分数阶导数引入Lagrange函数，可对非保守系统直接建立变分原理.分数阶微积分使得Lagrange力学、Hamilton力学、Hamilton－Jacobi理论等在同一框架下完整地得到描述［15］.

从上面的例子可以看出，有许多问题如果用整数阶导数来描述的话，或者不能得到合适的微分方程，或者所得到的微分方程非复杂，且所得到的结果与实际情况不一定非常吻合，而利用分数阶导数所得到的微分方程不但非常简洁而且利用它所得到的结果更接近实际.我认为，一个问题之所以复杂，有时候并不是因为它真的很复杂，而是因为没有找到合适的方法.利用分数阶导数而产生的分数阶微分方程就是这样一种研究复杂问题的有力工具.当然，关于分数阶微积分也有许多问题值得研究.比如说，最基本的问题是，经典的整数阶导数都有明确的几何和物理意义，但是对于分数阶微积分，人们至今也没有找到合适的几何和物理解释.但是它在研究实际问题中的作用是毋庸置疑的.也许，分数阶微积分就是二十一世纪的微积分［6］.

［1］Ross B.Proceedings of the International Conference on Fractional Calculus and Its Applications［C］.New York:Springer－ Verlag，1974.

［2］Oldham K B，Spanier J.The Fractional Calculus［M］.New York:Academic Press，1974.

［3］McBride S，Roach G F.Fractional Calculus［M］.Glasgow:University of Stratchelyde，1985.

［4］Samko S G，Kibas A A，Marichev O I.Fractional Integrals and Derivatives，Theory and Applications［M］.Switzerland:Gordon and Breach Sciences Publishers，1993.

［5］Podlubny I.Fractional Differential Equations［M］.San Diego:Academic Press，1999.

［6］Das S.Functional Fractional Calculus for System Identification and Controls［M］.Berlin:Springer－ Verlag，2008.

［7］Diethelm K.The Analysis of Fractional Differential E-quations，An Application－Oriented Exposition Using Differential Operators of Caputo Type［M］.Berlin－Heidelberg:Springer－ Verlag，2010.

［8］Caponetto R，Douglas G，Fortuna L，Petras I.Fractional Order Systems:Modelling and Control Applications［M］.New Jersey:World Scientific，2010.

［9］郑祖庥.分数微分方程的发展和应用［J］.徐州师范大学学报(自然科学版)，2008，26:1 －10.

［10］王在华.分数阶微积分:描述记忆特性与中间过程的数学工具［J］.科学中国人，2011，3:76－78.

［11］Debnath L.Recent applictions of fractional calculus to science and engineering［J］.International Journal of Mathematics and Mathematical Sciences，2003，54:3413－3442.

［12］Monje C A，Chen Y Q，Vinagre B M，Xue D Y，Feliu V.Fractional－order Systems and Controls:Fundamentals and Applications［M］.London:Springer－Verlag，2010.

［13］徐明瑜，谭文长.中间过程、临界现象——分数阶算子理论、方法、进展及其在现代力学中的应用［J］.中国科学 G 辑，2006，36:225－238.

［14］Mainardi F.Applications of fractional calculus in Mechanics［M］.Singapore:SCT Publisher，1997.

［15］Riewe F.Mechanics with fractional derivatives［J］.Physical Review E，1997，53:3581－3592.

Fractional calculus and its applications

ZHU Ben-shi
(College of Mathematics and Computer Science，Huanggang Normal University，Huangzhou 438000，Hubei，China)

This paper introduces the history，fundamental theory and applications of fractional calculus.

fractional calculus;fractional riemann-Liouville derivative;fractional caputo derivative;application

O175.1

A

1003-8078(2011)06-0001-03

2011-07-30 doi10.3969/j.issn.1003 －8078.2011.06.01

祝奔石，男，湖南邵阳人，讲师，博士，主要从事离散动力系统的研究.

黄冈师范学院博士基金项目(10CD089).

(张所滨)