浅谈职高数学的比较法教学

王捧林

（山西省阳煤集团职教中心 山西 阳泉 045000）

浅谈职高数学的比较法教学

王捧林

（山西省阳煤集团职教中心 山西 阳泉 045000）

比较法是数学思维最基本的方法之一，在课堂上科学合理地使用比较法，可以在数学教学中收到事半功倍的效果，对激活学生思维、提高学生能力也有着不容忽视的作用。

职高；数学；比较法；课堂教学

比较法是数学教学最常用的基本方法之一，其意义在于区分有关事物的共同点和不同点，以掌握事物的实质。在课堂上科学合理地使用比较法，对数学课堂教学能起到事半功倍的效果，对激活学生思维、提高学生能力也有着不容忽视的作用。笔者拟结合教学实践，从五个方面谈谈对数学课堂教学使用比较法的认识。

新旧比较，产生正迁移

学习知识的过程，是在已有知识的基础上重新建构的一个过程。当学习新知识时，若能够将旧的知识纳入新的认知结构，就会产生正迁移。新旧知识发生冲突时，将新的知识简单并入原有认知结构中，就会产生负迁移。

例如，从映射的角度定义函数与初中的函数定义相比较，可使函数中的关系由单一的解析式推广到非空数集中数x、y的对应关系，使函数的定义更深更广。通过比较可让学生理解到，以前学习的函数只是函数中的一类，是局部，更多的函数关系是不能简单地用一个x、y的等式来表示的，从而引导学生把旧知识并入到新概念中，产生正迁移。

再如，讲解平面向量中的向量运算时，从向量的概念出发，结合位移的定义得出向量相加的结果还是一个向量，与实数的加法与向量模的加法相对比，强调实数相加的运算结果仍然是实数，而向量模相加是两条线段长度的和即两个非负实数的和，可使学生清楚地认识到平面向量运算与实数运算是不相同的。在教学中及时与已有的相似概念、性质、定理加以对比，有利于正确理解新内容的实质，防止将新的认知结构并入原有认知结构中产生负迁移。

正反比较，揭示实质

正确理解概念是学习数学的基础，把握概念的实质是准确运用知识的前提。讲解概念时，从正反两方面进行强烈对比，勾勒出概念、定理的本质属性，可使学生更准确、更深刻、更完整地理解概念，把握概念的精神实质，避免使学生局限于对概念表象的了解，看似懂了，但遇到问题时就会失之毫厘，谬之千里。

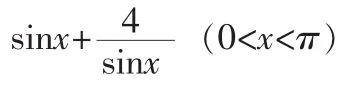
在课堂教学中尤其是对于概念定理的教学，不仅要正面引导，还要反面示错，通过正反比较、讨论、分析，深化对数学概念的认识，揭示概念的实质，真正使学生既知其然，更知其所以然，培养学生思维的深刻性。

是非比较，强化辨析

知识的学习是一个不断辨别正误、去伪存真的过程。鉴别是非的能力是数学能力的重中之重，只有在与谬误的对比中才能彰显正确。让是非同现一处进行比较，更易使学生在茫茫雾海中在灯塔的指引下坚定不移地驶向彼岸。

在课堂教学中巧妙地设计是非判断，通过比较使学生走出想当然的误区，可养成良好的学习习惯，做到遇事仔细斟酌，据理分析，从而切切实实地提高学生的鉴别能力。

共异比较，总结规律

数学问题千变万化，但万变不离其宗，总有规律可循。只要通过比较，细心找出不同问题的共同之点和相异之处，去其伪装，把握本质，分类归纳，摸索规律，就能收到事半功倍的效果。

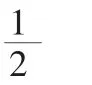
再如，解下列问题：（1）6个学生站成一排，其中甲乙不相邻，则不同的排法有几种？（2）6个人按照某种顺序排好，再插入2个人，有几种不同排法？

分析：两个问题的共同点都是要在“空”中插入人，属于分步问题；不同点是：问题1中两人不相邻；问题2中没有要求不相邻。所以：问题1中除甲乙外的4个人全排列，然后在4人形成的5个空位中任选2个位置插入甲乙，不同的排法数为；问题2中则需要在6人形成的7个空位中任选1空插入1人，然后在7人形成的8个空位中任选1空再插入1人，排法数为 7×8。

在课堂教学中，通过对题目或知识点的共异比较，可以使学生较深地认识知识的区别与联系，总结规律，归纳经验，能更准确、快捷地运用知识。

简繁比较，勇于探究

探究是数学的生命线，对数学题从不同的角度思考，可得到不同的解题方法。教学中应使学生掌握常规方法，还应有意识地引导学生思考寻求更美的解法，通过一题多解比较繁简，不仅可加深知识的纵横联系，还能培养学生的发散思维能力，挖掘创新潜能，形成探究意识，还能使学生在探究比较的过程中体验发现的快乐，体会到数学的美妙，从而懂得欣赏数学美。

例如，已知等差数列{an}中，前n项的和与前m项和相等，且n≠m，求sm+n。

函数方法：d≠0时，等差数列的前n项和公式可以归纳为二次函数式sn=An2+ Bn（n∈N*），其图像是函数y=ax2+bx图像上一群孤立的点。设A＜0，结合已知条件sm=sn，可标识出该数列中的几个关键点并画出图形，观察图形，可以清晰地看到：sm+n=0。

分析比较上面两种方法，常规解法思路顺畅，但运算繁杂。而换一个角度从数列与函数的关系入手，考虑sm+n=An2+ Bn的性质特征，结合抛物线的特性稍加思索，就能瞬间准确地解决问题。通过繁简比较，可引导学生转变视角，努力探索新途径，大胆探究创新，从而把数学学活。

总之，在课堂教学中根据教学内容、教学目标、教学要求，以及学生的知识结构、知识层次，灵活地采取比较教学法，可使学生思路清晰，思维严谨，思考深入，思想开阔，能收到良好的教学效果，并能提高教学质量。

[1]谢全苗.“由惑到悟”的数学课堂教学模式的构建与应用[J].数学教育学报，2009，（6）.

[2]魏良亚.加强学法指导，促进有效教学[J].中学数学月刊，2009，（1）.

[3]孙芸，曹军.剖析错解原因探究解题规律[J].中学数学，2006，（2）.

G712

A

1672-5727（2011）07-0115-02

王捧林（1974—），女，山西阳泉人，山西省阳煤集团职教中心讲师，研究方向为数学教育。

（本文责任编辑：王恒）