基于支持向量机的污水状态识别

张永利，朱艳伟

（1.河北理工大学 轻工学院，河北 唐山 063000；2.唐山师范学院 数学与信息科学系，河北 唐山 063000）

随着科学技术的发展，特别是微电子技术、集成电路及其设计技术、计算机技术、近代信号处理技术和传感器技术的发展，多传感器信息融合已经发展成为一个新的学科方向和研究领域。多传感器信息融合技术在军事领域和民用领域均得到了广泛应用。多传感器的信息融合层次有三种结构：数据层融合、特征层融合和决策层融合[1-2]。目前，信息融合常用的方法有，贝叶斯法、D-S证据理论法、聚类算法、人工神经网络法和模糊集合理论法等。但它们都存在着各自的缺点。支持向量机（support vector machine SVM）最初是由Vapnik提出的一种新兴的基于统计学习理论的学习机[3]。相对于神经网络的启发式学习方式和实现中带有的很大的经验成分相比，SVM 具有更严格的理论和数学基础，不存在局部最小问题。小样本学习使得SVM具有很强的泛化能力，不过分依赖样本的数量和质量，从而成为当前机器学习的一个研究热点。本文提出了一个新的多传感器信息融合方法：基于SVM的多传感器信息融合，并把此方法应用于污水状态的识别。

1 信息融合

多传感器信息融合方法多传感器信息融合要靠各种具体的融合方法来实现。在一个多传感器系统中，各种信息融合方法将对系统所获得的各类信息进行有效的处理或推理，形成一致的结果。多传感器信息融合目前尚无一种通用的融合方法，一般要根据具体的应用背景而定。归纳起来信息融合方法[1]主要有：估计方法、统计方法、信息论方法和人工智能方法。在人工智能方法中，人工神经网络方法是一种被广泛采用的方法。

基于神经网络的多传感器信息融合具有如下特点：具有统一的内部知识表示形式，通过学习方法可将网络获得的传感器信息进行融合，获得相关网络的参数（如连接权矩阵、结点偏移向量等），并且可将知识规则转换成数字形式，便于建立知识库；利用外部环境的信息，便于实现知识自动获取及进行联想推理；能够将不确定环境的复杂关系，经过学习推理，融合为系统能理解的准确信号；神经网络具有大规模并行处理信息的能力，使得系统信息处理速度很快。但是，神经网络也存在着缺乏严格的理论、数学基础，有局部最小值问题，训练过程难以掌握等缺点。因此，本文将一种新的理论——支持向量机，引入到信息融合中。

2 支持向量机

2.1 支持向量机

支持向量机是由线性可分情况下的最优分类面发展而来的。它的基本思想采用图1的二维情况说明。图中，实心圆点和实心三角分别代表两类样本，H为分类线，H1，H2分别为过各类中离分类线最近的样本并且平行于分类线的直线，它们之间的距离称作分类间隔（margin）。最优分类线指的是不但能将两类正确分开（即训练误差为零），而且能使分类间隔最大。

图1 最优分类平面

对于线性可分的样本集

满足：

支持向量机的数学表示式[4]为

其中，n是训练样本数。上面的问题被称为原问题。该问题能够通过标准的二次规划来解决。使用拉格朗日优化方法可将原问题转化为对偶问题得：

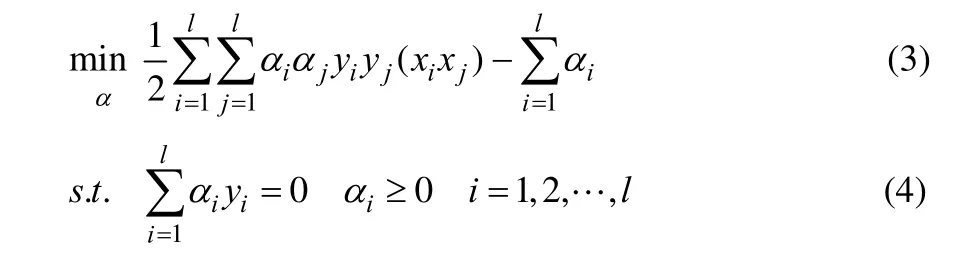
解出

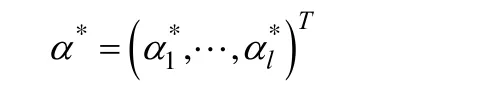
后，利用

并且选择α*的一个大于0的分量所对应样本(xi⋅xj)（即支持向量所对应的样本），根据

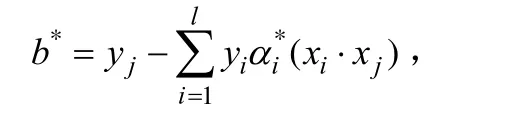
计算w和b以确定最优超平面 (w*⋅x) +b*= 0，由此求得决策函数

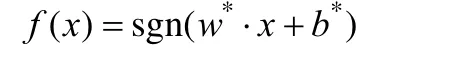
或

2.2 序列最小优化算法（sequential minimal optimization，简称SMO）

1998年，Platt提出了序列最小优化算法（SMO）来解决大训练样本的问题[5]，并和 Chunking算法进行了比较。该算法可以说是Osuna分解算法[6]的一个特例，工作集B中只有两个样本。其优点是针对两个样本的二次规划问题可以有解析解的形式，从而避免了多样本情形下的数值解不稳定及耗时问题，同时也不需要大的矩阵存储空间，特别适合稀疏样本。其工作集的选择也别具特色，不是传统的最陡下降法，而是启发式。通过两个嵌套的循环来寻找待优化的样本变量。在外环中寻找违背 Karush-Kuhn-Tucker条件（简称KKT条件）最优条件的样本，然后在内环中再选择另一个样本，完成一次优化。再循环，进行下一次优化，直到全部样本都满足最优条件。SMO算法主要耗时在最优条件的判断上，所以应寻找最合理即计算代价最低的最优条件判别式，同时对常用的参数进行缓存。

2.3 最小二乘支持向量机

为了使支持向量机能够对大样本情况进行学习，Suvkens J.A.K在1999年提出了一种新型支持向量机方法，最小二乘支持向量机（Least Squares Support Vector Machines，LS-SVM）[7]。该方法采用最小二乘线性系统作为损失函数，用等式约束代替传统方法中的不等式约束，通过求解一组等式方程，得出最优分类超平面，从而避开了求解计算量相对繁重的二次规划问题，并应用到模式识别和非线性函数估计，取得了较好的效果[8]，其运算简单，收敛速度快，精度高。

2.4 SVM多类分类器

一般SVM仅能够进行两类分类，目前，将SVM机器学习方法延伸到多类分类问题还处于初步研究阶段。已提出的解决该问题的思路有：1）构造多个2类分类器并组合起来完成多类分类，分成“one against one”和“one against all”两种类型；2）只使用一个SVM实现多个分类输出，这种思路涉及十分复杂的优化问题。

2.5 基于SVM的多传感器信息融合

多传感器的信息融合可以降低信息不确定性或降低信息模糊度，提高识别的正确率。在采用融合方法前，需对每个传感器的测量数据作相应处理（数据预处理和特征提取），然后利用SVM方法进行决策层的融合和分类。其过程为：根据实际系统要求，确定输入传感器的个数，采集各传感器数据，生成训练样本与测试样本，然后使用支持向量机对样本进行分类。

3 实验结果

城市污水处理厂日常监控数据来自 UCI数据库，数据库中有527组38维数据，共有污水状态13种。对数据进行预处理后得到全部属性和属性值都完整的记录有375个。由于记录中有些状态过少，为研究方便这里把性质相同的状态合并，合并后共有4种状态。首先，将样本分成两部分，其中245个样本用来训练分类机，130个样本用来测试分类机的分类识别效果。所有实验都是在个人计算机上进行的，计算机配置为，Intel(R) Core(TM)2 Duo T5470双核CPU，主频1.66GHz，1G内存和Windows XP操作系统，使用Matlab 7.0软件进行处理。

首先，使用信息融合常用的人工神经网络方法，选用BP网络进行实验，训练设定的目标值为0.01，训练次数设定为10000次。实验发现训练完10000次后目标还是没有达到。BP网络的测试结果：训练时间为118.92秒，仿真（测试）时间为0.063秒，测试样本的类别预测正确率为83.23%。

然后使用基于SVM的信息融合方法，支持向量机使用两种分类算法SMO算法和LS-SVM算法，因为合并后的污水状态为4种，这里采用“one against all”的多类分类方法。核函数选择的是Gauss径向基核函数：

通过实验对两种算法进行参数选取，得到实验结果见表1。

表1 BP神经网络与支持向量机的实验结果

4 结束语

BP神经网络算法的训练时间比较长，它的训练时间是支持向量机算法中的LS-SVM训练时间的420多倍，是支持向量机算法中的SMO算法的训练时间的7倍。花费了这么长的训练时间，但是得到的样本类别预测的正确率并不是很高，仅为83.23%。而SMO算法的正确率为90.77%，LS-SVM算法的正确率为 92.15%。可见支持向量机算法，在面对污水处理监测数据的这样的模式识别问题有很大的优越性。因此，将支持向量机引入到信息融合问题中具有可行性。