兆瓦级变速恒频风电机组转矩PI控制策略
刘 琳, 董祖毅
(上海电气输配电集团,上海200042)
作为解决能源和环境问题的有效途径,风力发电正在世界范围内得到快速发展,已日益成为当今世界速度增长最快的能源[1]。自20世纪90年代后,变速恒频风电机组得到迅速发展。与定速风电机组相比,变速风电机组可以有效提高风能利用效率,并保证了风力机输出功率平稳[2]。变速控制指的是发电机转速可以随风速而变化,从而实现最大风能捕获;额定风速以上时,变桨控制可以有效调节风力发电机组吸收功率及叶轮产生载荷,使其不超过设计的限定值[3]。
变速恒频风力发电机组的控制主要为额定以下的转矩控制和额定以上的变桨控制。如何从转矩控制区过渡到变桨控制区,是非常关键的技术问题,常用的方法是采用转矩-转速斜线控制。然而,让风力机运行在这条很陡的斜线上是非常困难的,转矩对转速的变化非常敏感,势必造成在此运行区域附近转矩上下波动很大。近年来,比例积分(Proportion-Integral,PI)控制器越来越多地应用到转矩控制中,是目前的主流研究趋势。相比于很陡的斜线过渡区,转矩PI控制策略可以在更宽的风速运行范围内工作在CPmax点附近,与同样最大工作转速相比能吸收更多的能量,同时保持了风力机控制系统的一致性[4]。
本文在建立风力机模型以及传动链模型的基础上,设计了额定风速以下的转矩区控制策略。分为3个运行区域:最小转速运行区、最佳叶尖速比区和额定转速运行区。其中,最小转速运行区和额定转速运行区均为PI控制,其控制结构和参数相同,最佳叶尖速比区根据理论公式以及机械损耗计算发电机转矩。以某2MW风力发电机组的系统参数为例,对建立的模型和控制系统进行了仿真研究,取得了良好的控制效果。
1 变桨距风电机组建模
1.1 风轮模型
当自然风以风速v轴向流向风轮时,风轮从风能中捕获的功率[5]为

式中,Pr为风力机实际获得的轴功率,W;风能利用系数CP为风力机从自然风中吸收能量的利用率大小;β为桨距角;叶尖速比λ为风轮在不同风速中的状态,用叶片的叶尖圆周速度与风速之比来衡量,其表达式为

式中,fW为风轮的转速,r/s;ωW为风轮角速度,rad/s;ρ为空气密度,kg/m3;v为风速,m/s;R为风轮的半径,m。
1.2 传动链模型
在传动链中,齿轮箱是传动柔性的主要来源,故将风力机与齿轮箱等效为一个质量块,发电机转子等效为另一个质量块,而将传动柔性等效至高速轴,从而建立两质量块模型[6]。模型示意图如图1所示。

图1 轴系两质量块模型示意图
图1中,JW为风力机转动惯量;DW为风力机阻尼系数;TW为风力机转矩;θW为风力机转角;Ts为传动轴转矩;k为传动轴刚度;JG为发电机转动惯量;DG为发电机阻尼系数;TG为发电机转矩;θG为发电机转角;ωG为发电机角速度。
根据轴系振动原理,可以得出传动链的轴系运动方程,各参数均已经折算到高速轴侧。

2 变速恒频风电机组的控制系统设计
在额定风速以上时,设计变桨PID(比例-积分-微分)控制器实现恒定的最大功率Pmax输出;在额定风速以下时,设计转矩PI控制器实现并网最小转速运行区和额定转速区的平滑控制,保证了整个工作区的控制系统一致性,图2为控制系统原理图。

图2 控制系统原理图
图2中,T′W为经传动链之后的机械转矩;ω为发电机转速;S为拉氏算子;β′为变桨控制器的输出桨距角;ωset为发电机转速设定;KP为变桨控制器比例系数;KI为变桨控制器积分系数;KD为变桨控制器微分系数;βmax为桨距角上限;βmin为桨距角下限;ξ为变桨系统等效阻尼比;ωn为变桨系统等效自然振荡频率。
2.1 变桨距控制
当风速变化时,风力机运行点要相应改变。额定风速以上时,为了实现恒功率输出,同时保持传动系统良好的动态特性和稳定性,风力机将调节其桨距角,发电机转矩需求设置为额定值。风力发电机组的桨距控制系统通常采用转速PID控制器,其参数根据实际风力机参数进行调整,P控制可以快速跟随输入信号变化,I控制消除稳态误差,D控制抑制动态扰动。
2.2 转矩控制
本文重点设计额定以下的变速区域的转矩控制策略,以及在额定点附近转矩控制器与变桨控制器的切换:通过逻辑开关控制在额定以下时转矩控制器工作、额定以上时变桨控制器工作,当风速变化剧烈时,两个控制器一起配合工作。通常,根据风力机物理特性和现场需求设计具体的逻辑开关。转矩与转速的关系曲线如图3所示。
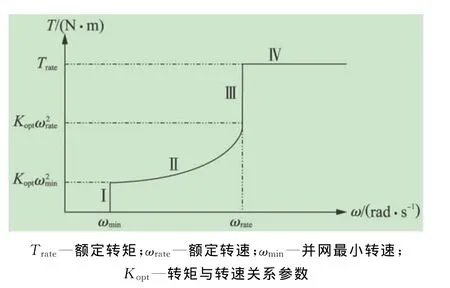
图3 转矩-转速关系曲线
如图3所示,在额定风速以下时,发电机运行在变速控制方式。该工作区域的主要目的是调整发电机转速以期实现最大风能追踪控制。但是由于受到本身物理特性的影响,发电机的输出受到两个基本限制:转速限制和功率限制;因此,该阶段风力机运行在3个阶段:最小运行转速区(Ⅰ)、最佳叶尖速比区(Ⅱ)和额定转速运行区(Ⅲ)。最佳叶尖速比运行区内,转矩与转速的平方成正比例关系,可以根据理论公式以及机械损耗计算。对于最小运行转速区和额定转速运行区的转矩控制,目前常用的方式是用很陡的过渡斜线来表示转矩与转速的关系,该方式简单易行。但是,在这个很陡的过渡斜线上,转矩对转速的变化非常敏感,影响了输出功率的平稳性。
本文设计的转矩PI控制器,特别是额定转速区的PI控制器,可以显著改善机组性能。风力发电机组可以在很宽的风速范围内工作在CPmax附近,比同样最大工作转速时吸收更多的能量。转矩PI控制器实现了控制系统的一致性,在额定风速附近的转速控制更加平稳。
在最佳叶尖速比运行区,理论上的发电机转矩计算如下:

式中:λopt为最佳叶尖速比;CPmax为最大风能利用系数;n为齿轮箱变比。

本文设计的转矩PI控制器的基本结构如图4所示,其中,Δω为转速偏差,T为PI控制器输出转矩,Tmax为转矩上限,Tmin为转矩下限。在转矩PI控制策略中,PI控制器的输入为发电机测量转速与额定转速的偏差,PI输出值受到上下限约束,上限为额定转矩,下限根据式(5)以及机械损耗进行计算。

图4 转矩PI控制器原理图
3 仿真分析
本文基于Matlab/Simulink环境进行仿真,根据风机的气动方程以及传动链模型搭建了线性化模块。对转矩PI控制器的仿真主要在额定风速附近进行湍流风仿真,PI控制器参数根据某2MW变速恒频双馈机组实际参数调试得到,风力机参数见表1所示。
图5~7分别为平均风速为9、10、11m/s,湍流密度为10%的湍流风仿真结果,仿真时间600s。

表1 风力机参数

图5 平均风速=9m/s时的仿真结果


图6 平均风速=10m/s时的仿真结果

图7 平均风速=11m/s时的仿真结果
结果表明:转矩PI控制器的效果显著,转速比较平稳,没有完全随风速变化而快速波动,避免了高频振动,提高了机组的稳定性。在额定风速以下,运行在最佳叶尖速比区,额定风速以上运行在变桨区,在额定风速附近时转矩PI控制器与变桨控制器相互配合作用,发电机运行在额定转速,保证了在较宽风速范围运行在最佳叶尖速比,提高了发电效率。
4 结 语
本文在分析变速变桨距风力机组工作原理的基础上,建立了风力机气动模型以及传动链模型。从工程优化设计角度出发,设计了额定风速以下的转矩PI控制器。将额定风速以下的风力机工作区域划分为3区:最小运行转速区、最佳叶尖速比区和额定转速区,使得风力机在较宽的风速范围内运行在最佳叶尖速比,并获得了更多的能量。在Matlab/Simulink环境下,搭建了单台风电机组仿真模型。以2MW风力发电机组为例,在多种风况下进行了仿真测试,结果表明该转矩PI控制器具有良好的稳定性和动态性能。
[1]World Wind Energy Association.Worldwide wind energy capacity at 39.151MW-7.981MW added in 2003[EB/OL].(2004-03-05)[2007-11-16].http://www.wwindea.org.
[2]叶杭治.风力发电机组的控制技术[M].北京:机械工业出版社,2002.
[3]刘湘琪.风力发电机组电液比例变桨距控制系统的研究[D].杭州:浙江大学,2004.
[4]Bossanyi E A.Electrical aspects of variable wind speed operation of horizontal axis wind turbine generators,ETSUW/33/00221/REP[R].Harwell,UK:Wind Energy Group Ltd,1994.
[5]贺德馨.风工程与工业空气动力学[M].北京:国防工业出版社,2006.
[6]李东东,陈 陈.风力发电机组动态模型研究[J].中国电机工程学报,2005,25(3):115-119.

