《直线与圆的位置关系》的教学反思

◆顾凤光

(吉林信息工程学校)

《直线与圆的位置关系》的教学反思

◆顾凤光

(吉林信息工程学校)

《直线与圆的位置关系》应用比较广泛，是几何知识的一个综合运用，在今后的解题及几何证明中，将起到重要的作用。虽然内容比较简单，相对比较容易理解，但是仍然有些让学生感觉困惑的地方，对此进行了教学反思。

直线与圆 位置关系 教学反思

教学目的:

1.使学生理解直线与圆相交、相切、相离的概念，掌握直线与圆的三种位置关系的定义及其判定方法和性质。

2.通过直线与圆的三种位置关系的研究，向学生渗透对比、数形结合的思想，培养学生观察、分析、总结及解决问题的能力。

教学重点:

掌握直线与圆的三种位置关系的性质与判定及应用。

教学难点:

引导学生得到两个数量d和r，并加以比较，从而达到直线与圆的三种位置关系的性质和判定的正确运用。

关键:

根据点和圆的位置关系，即点到圆心的距离d和半径r之间的大小关系，从而推导出用圆心到直线的距离d和半径r之间的关系来确定直线与圆的三种位置关系。

教学手段:

多媒体教学的运用。

一、教学过程

1.复习提问:

点与圆有几种位置关系?如何判断点与圆的位置关系?

其中:r指的是圆的半径，d指的是点到圆心的距离。

2.引入

问:让学生自己动手画图，过圆外一点做一条直线，此直线与圆有几种位置关系，各有几个公共点?

引导学生总结归纳:

定义:由直线与圆的公共点个数，得出直线与圆的三种位置关系:

①相交。直线与圆有两个公共点时，叫做直线和圆相交，这时直线叫做圆的割线。

②相切。直线与圆有唯一公共点时，叫做直线和圆相切。这时直线叫做圆的切线，唯一的公共点叫做切点。

③相离。直线与圆没有公共点时，叫做直线与圆相离。

强调:直线与圆有唯一公共点时，直线和圆相切是指直线与圆有且只有一个公共点，它与直线与圆有一个公共点含义不同。

例1:判断直线2x－3y+1=0与圆x2+y2=1的位置关系?

分析:数形结合可以看出，通过圆心到直线的距离d与圆的半径r进行比较即可

解:圆心(0，0)，圆半径r=1，圆心到直线2x－3y+1=0的距离为

因此所给直线与所给圆相交

练习:判断下列各直线与圆的位置关系?

1.直线x－3y+2=0与圆x2+y2=2

2.直线3x+4y－20=0，圆(x+1)2+(y－2)2=9

3.直线 x+2y－10=0，圆 x2+y2－3x+5y+7=0

练习中第1、2题可根据例1求出圆心及圆半径，然后进行比较判断，练习中第3题所给圆的方程是一般式，可将方程经过配方化为标准式，然后再解。

解题关健:利用点到直线距离公式，准确求出圆心到所给直线的距离。

解题过程略。

答案:1.相交 2.相切 3.相离

变形:已知:如图示，∠AOB=300，M为OB上一点，以M为圆心，5cm长为半径作圆，若M在OB上运动，

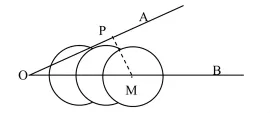
问:①当 OM满足____________时，⊙M与OA相离?②当OM 满足____________时，⊙M与OA相切?③当OM满足___________时，⊙M与OA相交?

分析:结合图形可以看出，此时圆的半径固定，圆心是动点，导致圆心与射线OA的距离在变化，当⊙M与OA相交时圆心到射线OA的距离小于圆半径;当⊙M与OA相切时圆心到射线OA的距离等于圆半径;当⊙M与OA相离时圆心到射线OA的距离大于圆半径，因此，要判定射线OA与圆的位置关系可由M点向射线OA做垂线段MP，因为∠AOB=300则MP=，若0＜MP＜5cm=r时，则⊙M与OA相交。若MP=5cm=r时，则⊙M与OA相切，若MP＞5cm=r时，则⊙M与OA相离，故可相应推出OP的值。

解题过程略。

例2.求过点p(1，－1)的圆x2+y2－2x－2y+1=0的切线方程

总结:过一点求圆的切线方程时，一定要先判定点所在的位置，点在圆上还是圆外的解法是不同的。另外，点在圆上时切线只有一条，点在圆外时切线一定有二条。

练习:

1.求经过直线x+3y+7=0与3x－2y－12=0的交点，圆心为(－1，1)的圆的方程

2.求经过原点的圆(x－2)2+y2=1的切线方程。

课堂小结:

本节课主要学习了直线与圆的三种位置关系即相离、相切、相交及直线与圆的位置关系的判定和性质，让学生完成下表。

?

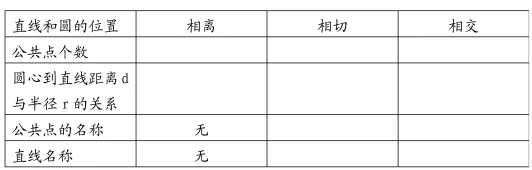
分层作业:

1.求过点p(1，－5)的圆x2+y2+2x－y=17的切线方程。

2.求过点p(－1，2)的圆x2+y2+4x=1的切线方程。

3.已知 Rt△ABC 的斜边 AB=5cm，AC=4cm

(1)以点C为圆心作圆，当半径为多长时?AB与⊙O相切

(2)以点C为圆心，分别以2cm和3cm的长为半径作两个圆，这两个圆与AB分别是怎样的位置关系?

4.求与x轴相切，圆心在直线3x－y=0上，且被直线x－y=0截得的弦长为的圆的方程。

前两道作业题面向全体学生针对本节课的知识加以巩固训练，后两道题的综合性比较强。可以培养学生综合解题的能力，适应高考的需求，满足他们的求知欲，培养学生分析解决问题的能力。