套餐商品分析的实践意义
——以河北某肯德基餐厅套餐为例
闫静怡
套餐商品分析的实践意义
——以河北某肯德基餐厅套餐为例
闫静怡
套餐商品不是简单的商品组合,其独立性和完全分解性决定了它具有不同于联产品、复合商品和产品组合的独特性质,对它的研究应从其性质出发,不拘泥于传统数量分析和模糊数量分析,应针对套餐商品的组合性,将离散数学中的组合论引入研究。以肯德基套餐商品为例,运用集值函数、集值分析、集合运算和集合关系等方法,对套餐商品的投入成本进行数量分析,并以此证明在经济管理学研究和实践中,不仅应开拓套餐商品这一新的研究领域,而且应让组合论这一数学分析方法占有一席之地。
套餐商品;特殊性;组合论;数学分析方法
套餐商品是指打包销售、具有独特价格和种类构成的一些商品的组合。本文将“商品”指代为可以按照特定价格交易的物品。
一、套餐商品的独特性质
套餐商品所含商品具有独立性和完全分解性的特征,这使套餐商品完全区别于联产品、复合商品与商品组合。
(一)套餐商品所含商品的独立性和完全分解性
第一,套餐商品所含商品具有独立性,套餐商品中的任何商品的存在都不依赖于套餐商品的存在。例如肯德基“香辣鸡腿堡套餐”中所含的汉堡、薯条和饮料中任意一种,都不是依赖于其他两种才能存在,没有了薯条和饮料,汉堡并不消灭;同时,套餐商品所含的所有商品价格的确定也都不依赖于套餐商品 (相反,在大多数情况下,套餐商品的定价要以组成它的商品单价的总和为基础),例如中国电信的“3G手机上网业务套餐”,其中包含的通话服务和上网服务可以单独销售,但其价格不能以套餐内价格为基础。这种独立性使得套餐商品不同于商品组合。对套餐商品的研究立足于其独立性,探索独立商品组合到一起后产生的价格节余会给包括生产销售者和消费者在内的市场主体带来怎样的激励。而商品组合是由一个厂商经营的全部商品构成,它本身是一个生产销售者的概念,出发点是如何对产出或销售的商品进行合理的结构设计,来取得最大化收益。因此,套餐商品和商品组合的研究目的和研究方法大不相同。
第二,套餐商品所含商品具有完全分解性。套餐商品中所含的所有商品都具有独立的商品价值,可以脱离套餐商品,以独立价格销售。仍以肯德基“香辣鸡腿堡套餐”为例,汉堡、薯条和饮料在一次交易中可能被组合到一起当作套餐出售,也完全可以各自分开,当作单品销售。首先,这种完全分解性让套餐商品区别于联产品。联产品是联合生产中的不同产品所构成的产品组合。“联”的意义就在于生产过程中,不同商品会同时被生产出来(如生产香蕉果肉必然会生产香蕉果皮),从而构成联合或连带关系。而套餐商品所含的商品之间不存在这种连带关系,它们随时可以分开成为独立商品。其次,这种完全分解性让套餐商品区别于复合商品。“复合商品”指不同用途、不同效用的复合体。“复合”可能指的是商品使用价值的复合,如一根木棍既可以擀面,又可以做撑杆;也可能指的是商品由不同零件复合,如一盏台灯由灯座、灯管和插销复合而成。无论是哪种复合,均与套餐商品的完全分解性大相径庭。套餐商品所含每个商品均有独立使用价值,可以拆分成单独的使用价值进行交易,而要以使用价值把一个复合商品分解开来在大多数时候做不到;套餐商品所含商品分开之后,完全不影响各自的使用价值和交易价格(而且一般分出的商品单卖要比在套餐中时价格高,这也正是套餐商品价格节余的意义所在),复合商品的零件拆分后会完全丧失其在复合商品中才能产生的使用价值,从而其交易价格也会大打折扣。
套餐商品构成的独特性质,使我们有必要将它作为一个新的研究对象作进一步研究。在研究方法的确定中,套餐商品所导致的消费成本的特殊性是必须重视的问题。
(二)套餐商品消费成本的非理性和不可加性
首先,价格节余必然导致消费成本的不可加性,也就是若干个消费的独立支付成本之和不恒等于这些消费的共同支付成本。套餐商品的价格低于组成它的所有单品价格之和,这就使我们研究套餐商品及含有套餐商品的商品混合时,不能按数量乘以单价再简单相加的办法去确定需求的消费成本。这种不可加性使我们无法以传统的数量方法研究套餐商品,因为该方法应用的重要前提正是“可加性”,严格要求需求中每种商品独立支付的成本之和等于它们共同支付的成本,以此为基础讨论需求和供给。由此可见,虽然套餐商品的价格结余带来了经济效用的提高,但也致使传统的数量方法在其研究上无用武之地。
其次,价格节余导致了套餐商品消费成本的非理性。非理性是指一个需求较大的消费可能具有低于某个需求较小的消费的成本。套餐价格低于组成它的较小商品价格之和,正是非理性的一种体现。这种非理性使得模糊数量分析方法亦不适用于对套餐商品的数量研究。因为模糊测度虽不要求标的具有可加性,却严格要求测度对象具有有序性,即较大集合的度量不能低于较小集合的度量。也就是说,要将模糊数量分析方法引入套餐商品研究,套餐商品的价格必须大于等于组成它的全部或部分商品之和,而这个前提无法成立。
二、将组合论方法引入套餐商品研究
下面以肯德基的套餐商品为例,说明套餐商品及其数学分析方法的实践意义。既然是从商品的“组合性”出发,那么需要细化研究对象的组合性质。肯德基套餐商品有这样的性质:它由主菜(各类汉堡或炸鸡)和配菜(饮料和小食)组成(“肯德基套餐”指的是“蔬果搭配餐”,不包括“儿童套餐”)。其中,每款套餐的主菜各不相同,而配菜却完全相同。主菜不同使套餐之间具有不可替代性,也就是说,对特定的消费需求,如果不选择相对应主菜所在套餐,就只能单点主菜;而这却不一定意味着单点配菜,因为各套餐配菜完全相同,所以单点主菜后剩余的配菜需求可以通过其他套餐来满足。
针对上述特点设计这样一个消费需求:它含有2种可组成套餐的主菜,并且所组成的2种套餐的价格节余不相同;同时,它含有的配菜需求不小于每种配菜的需求并不大于2种主菜需求的总和。这样设计的目的是既保证套餐可以选择,又限制套餐选择的数量,以观察在一个需求不能完全被套餐所满足时,如何组织商品结构才能使消费达到最小化。将套餐商品价格与其所含商品单点价格之和的差额称为价格节余,为阅读方便,以表格的形式列出消费需求,可选套餐和单品价格,以及商品组合方案:

表1 商品需求表 (单位:个)
针对上述需求,将可选商品列入表2,并按价格节余从大到小的顺序自左向右排列。其中,嫩牛五方套餐中含1个嫩牛五方,1包薯条,1杯九珍果汁;香辣鸡腿堡套餐中含1个香辣鸡腿堡,1包薯条,1杯九珍果汁。
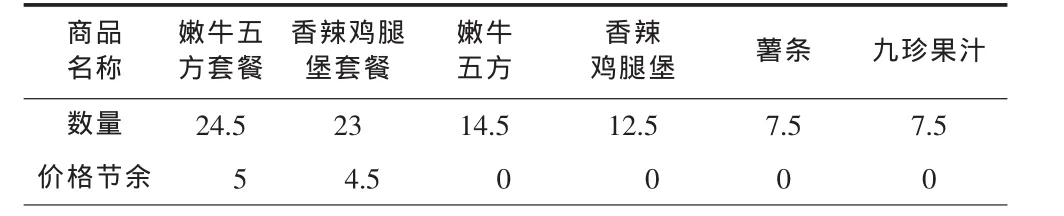
表2 商品价格表 (单位:元/个)
商品投入方案及其总成本如下:
可以看出,方案“一”是消费成本最小的方案,其特点是:它优先投入了嫩牛五方套餐,尽可能多地使用这种价格节余较大的套餐;之后,在剩余的产品需求中,又优先投入并尽可能多地使用价格节余第二大的香辣鸡腿堡套餐;最后,在没有价格节余的套餐商品后,以单点的方式,投入没有价格节余的商品,最后实现需求全部满足。
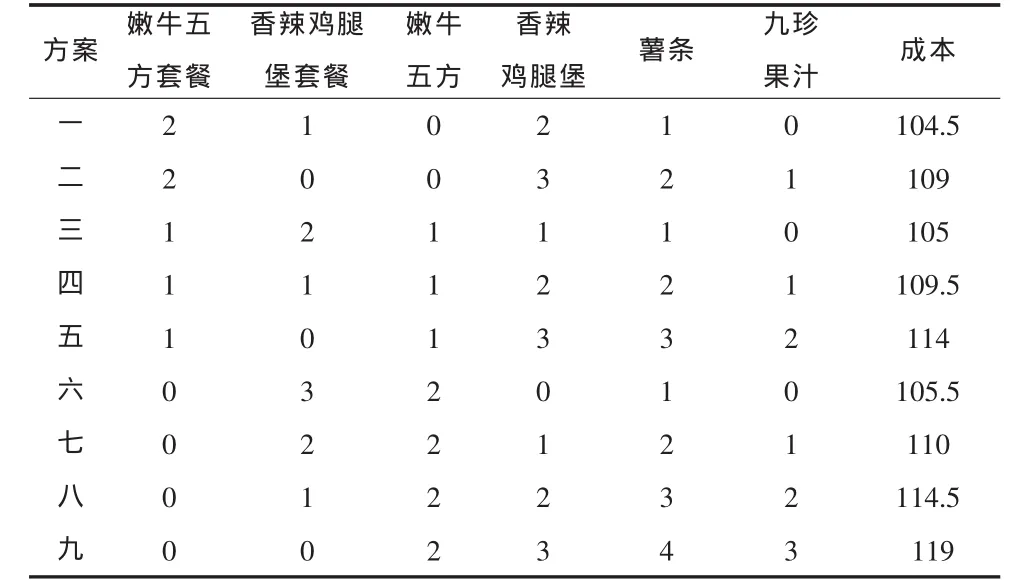
表3 满足需求的商品投入方案及其总成本
这种结果的出现不是偶然的,可以通过数学方法去证明它。肯德基套餐可以分为主菜和配菜两部分。设一个消费结构中有两种套餐商品1和2,其中主菜的价格节余为X1和X2,配菜价格节余为Y1和Y2,对它们投入的数量为N1和N2,则该投入总的价格节余为:
N1+X1+N2X2+N1Y1+N2Y2
设套餐1价格节余大于套餐2,即
X1+Y1+X2+Y2
因为各套餐中配菜完全相同,即它们具有相同的价格节余,Y1=Y2。 那么,上式两边同时减去Y1和Y2,得到:
X1〉X2
也就是说,套餐商品价格节余差异来源于套餐中所含主菜的价格节余差异。既然套餐中配菜的价格节余是无差异变量并恒等于一个常数,在讨论套餐投入方案而进行价格节余比较时,就可以将配菜的价格节余设定为0,即认为套餐的价格节余全部出在主菜上,其配菜本身没有价格节余,但只有购买配菜才能享受主菜的价格节余。此时总价格节余量的式子可以简化为:
N1X1+N2X2
最优的投入方案,就是能让上式取得最大值的方案。因为肯德基套餐之间不可替代,每种主菜不包含在其他套餐中,所以可以确定,此时X1和X2也都是常数,即它所在套餐的价格节余。所以,需要确定N1和N2的投入数量,使上式取得最大值。
配菜虽然在价格节余上对投入无影响,却在需求数量上影响投入方案设计。我们已经设定配菜需求不小于每种配菜的需求并不大于2种主菜需求的总和。有了这种限制,就不能通过套餐完全满足主菜需求,按主菜需求点相应数量的套餐,必然导致超出需求的配菜出现。在此情况下,两种套餐投入数量之和的最大值只能是配菜需求的最小值。设配菜需求最小值为N,则有:
N1+N2≤N
设优先投入价格节余较大的套餐商品时,N1=a1,N2=a2,总价格节余为:

我们只需证明上面的价格节余大于其他任何方案产生的价格节余即可。优先投入的意思是“尽可能多地投入价格节余较大的商品”,而套餐投入的总数量受配菜需求量的限制,所以容易看出,在上式中,a1+a2=N,也就是N1+N2的最大值。 即:
N1+N2≤a1+a2
商品1因价格节余较大而被优先投入了,所以此时a1是a2可取的最大值。即在其他投入方案中,商品1的投放量N1=(a11)(0≤n≤a1)。 将这个式子代入上式,得到:
N2≤a2+n
因为N1值已经确定,所以要使总价格节余最大化,N2应取最大值,此时总价格节余为:

(1)-(2),得:
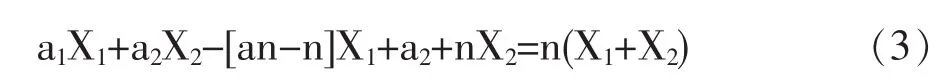
因为X1〉X2,所以(3)式恒大于0,即优先投入价格节余较大的套餐商品,才能实现总价格节余最大,消费成本最低。
不过,这个结论只适用于肯德基套餐结构下的商品。缺乏了“套餐间的不可替代性”和“配菜的完全一致性”这两个因素,套餐组成商品的价格节余就不那么清晰,从而使仅根据套餐商品价格节余的大小来决定优先投入的方法不一定能达到消费成本最小化。比如套餐间主菜有交叉时,设“嫩牛五方套餐”中多含2个香辣鸡腿堡,售价49.5元,此时两个套餐价格节余都未变,而优先投入“嫩牛五方套餐”的消费方案“一个嫩牛五方套餐、一个香辣鸡腿堡套餐,一个嫩牛五方,一包薯条”的成本109.5元,并不大于优先投入价格节余较小的“香辣鸡腿堡套餐”的消费方案“3个香辣鸡腿堡套餐,2个嫩牛五方,1包薯条”的成本105.5元。在这些情况下如何使投入方案最优,则是需要进一步探讨的问题。
三、套餐商品及其数学分析方法的实践意义
套餐商品及其数学分析方法开拓了经济管理学研究的新领域,同时,至少是在肯德基套餐这种类型的套餐商品交易上,也具有重要的实践意义。
第一,套餐商品的应用实现了信息的平等和公平。商家和顾客几乎在同一时刻掌握同样的套餐商品价格节余信息;所有顾客也通过“挂在墙上”的方法得到同样的信息,从而指导理性消费行为。
第二,数学分析方法的应用实现了信息的准确和对称。组合论的数学分析方法尽管在理论证明上复杂,在实际应用中却很简便易行,容易为商家和消费者运用。使他们能够在选择套餐商品时精确计算出价格结余,从而为供销行为做出理性指导。
第三,套餐商品能够实现商家和消费者的利益最大化,实现帕累托最优。因为信息的完美,消费者可以最少成本满足需求,而消费者消费需求的提高也为商家带来了收益。除此之外,套餐本身的结构设计也使得商家成本节约和消费者需求满足同时实现。
[1]Piero Sraffa.production of commodities by means of commodities[M].Cambridge Press,1963:50.
[2]约翰·贝茨·克拉克.财富的分配[M].邵大海,译.海口:南海出版公司,2007:201.
[3]Halmos R.Measure Theory[M].Paul Springer-Verlag Berlin Heidelberg,New Yark,1974.
[4]赵晓冬.集合商品投入分析[M].北京:科学出版社,2009:77.
[5]赵晓冬.联合生产与联合商品成本分析[J].数量经济技术经济研究,2001(12).
[6]帕尔格雷夫.经济学大辞典:第3卷[M].北京:经济科学出版社,1996:1053.
F760
A
1673-1999(2011)13-0094-03
闫静怡(1985),女,河北唐山人,硕士,燕山大学(河北秦皇岛 066004)政策与发展规划处实习研究员,研究方向为法律经济学、公共管理。
2011-04-19
河北省社会科学基金资助项目“河北省服务产品套餐及其效用优化研究”(HB10XGL172)。
——配菜
——配菜

