RHIC能区粒子分布特征与中心度关系的研究

魏新兵 冯笙琴

（三峡大学 理学院，湖北 宜昌 443002）

随着高能重离子碰撞的能量愈来愈高，人们普遍认为高能QCD能够进入一个新的量子态［1－5］，被称为色玻璃凝聚态（color glass condensate，CGC）.这种态的主要特征表现为强的相干胶子场，并由此导致碰撞系统的胶子饱和［1－5］.最早提出 CGC观点是 HERA实验组［6－8］，他们发现随着碰撞能量的升高，分数动量x的减小（或四动量转移Q的增加）胶子密度函数xG（x，Q2）迅速上升.胶子密度的迅速增加可以归功于QCD的非阿贝尔特性和胶子带有色荷.随着能量越来越高，对应的x将会越来越小和Q越来越大，相应的胶子密度将以log（1／x）形式增长.

由于QCD的非线性特征，胶子簇射会产生更多的胶子簇射，这将引起在小x区域，胶子数目快速增长，也即是强子内的每单位体积每单位快度的胶子密度随着x减小，呈现出指数增加.但是由于胶子作用的非线性特征，可以推测随着碰撞能量的进一步升高，胶子的横向密度在每一确定的Q2时，将达到饱和，这即是在足够高能量时的所谓胶子饱和现象［1－5］.

主要讨论高能重离子碰撞的胶子饱和，以及末态粒子的时空演化特征.随着对撞能量升高到超相对论量级，碰撞核在纵向的洛伦兹收缩效应越来越明显，碰撞核类似于带色胶子薄片，如图1所示（箭头表示极化的矢量胶子）.在图1中，胶子由带箭头的矢量表示，箭头方向表示胶子的极化方向.这两块极端相对论收缩的薄片很容易相互穿透，留下熔化的色玻璃态，形成夸克－胶子等离子体.

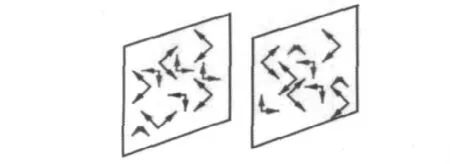
图1 两带色薄片碰撞示意图

对于饱和的色玻璃态，其固有形成时间标度τ为饱和动量的倒数.对应在 RHIC能区，1／Qs～0.2fm／c～5×10－25s.对于大动量（或大快度）的粒子，时间标度在纵向存在洛伦兹延迟.这意味着，慢（较小快度）粒子会先产生，并位于中心快度区域，而快（较大快度）粒子会后产生，并产生于远离中心快度的区域（见图2）.在文献［9－10］中，已建立了高能重离子碰撞的胶子饱和物理图像，并给出了胶子快度分布，文献［9－10］认为产生粒子时空演化作用对末态粒子分布影响有限，忽略了产生粒子时空演化作用.但通过认真分析他们拟合RHIC能区结果发现，文献［9－10］能较好解释中心快度区域的快度分布，但对偏离中心快度区的结果拟合的不好.本文通过考虑产生粒子流体力学时空演化对文献［9－10］的色胶子饱和模型进行了修正.

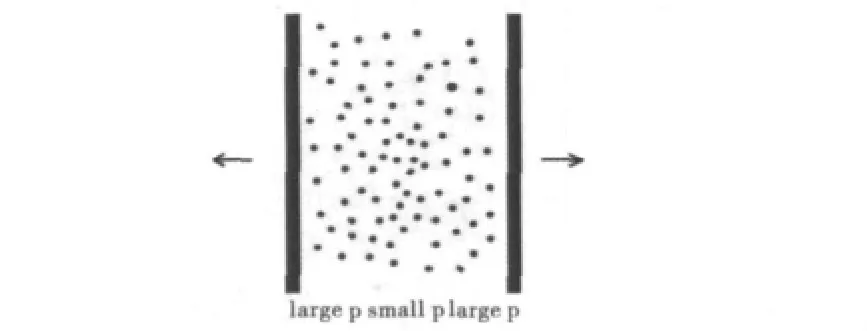
图2 两核碰撞后的粒子产生示意图

本文的具体安排如下，首先介绍胶子饱和模型，然后在此基础上引入强子流体的时空演化，给出粒子的快度分布特征；并在此基础上与实验进行比较.

1 考虑强子流体时空演化的胶子饱和模型

与上文所述，相对论重离子对撞机（RHIC）产生的高能量可以使物质进入了一个新的相－胶子饱和态［1－5］.胶子饱和态描述的是核在碰撞前的一种状态，通过核内带色的无质量胶子在不断发射胶子，胶子不断地聚集，使得胶子的相空间密度足够高，随着碰撞能量的升高，部分子将不断激发，核中部分子密度将会越来越大，部分之间的距离将会越来越小，最后将会趋近于一个定值，对应一个，此时系统达到一个临界态，即饱和态.此时用一个动量Qs来表征，为胶子饱和的标度动量.

对于两个相向运动（即将碰撞）的核来说，每一个核都有一个饱和度［9－10］，即 Qs（A1），Qs（A2），定义［9－10］：

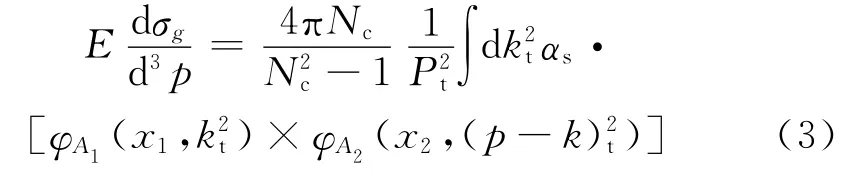
其中，x1，2＝，αs为跑动耦合常数；kt是碰撞前核中的胶子的横动量，pt是产生胶子的横动量；φ（x，）是描述了核中给定的横动量kt和动量分数x找到的胶子的几率［9－10］；φ（x，kt）与胶子结构函数之间的关系为

上式表明产生胶子的结构函数是碰撞前单个核中的胶子分布函数的在某一横动量区的平均值.

则胶子的快度分布为

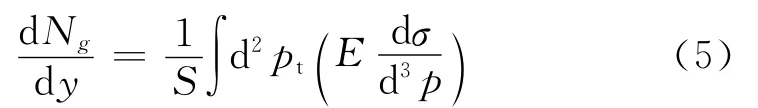
其中，S为非弹性散射截面.在式（3）中，kt积分区域分为两个部分，kt≪pt和，于是，

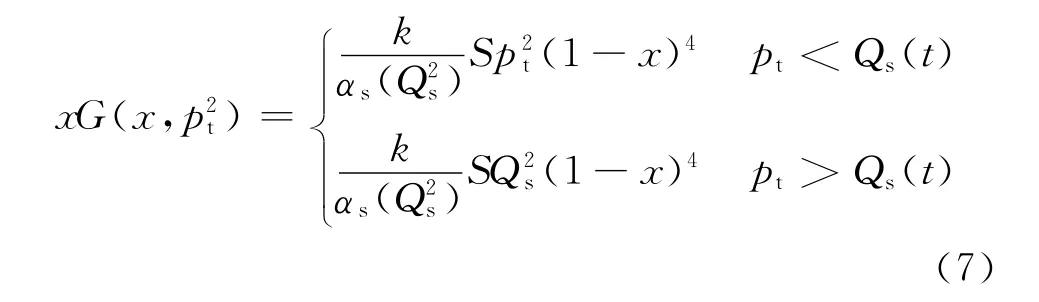
下面对pt区间进行分区：

（1）pt＜Qs，min.在这个区域内，核 A1与A2核都在饱和区；

（2）Qs，min＜pt＜Qs，max.在这个区域内，核A2处于饱和区，而核A1处于不饱和区；

（3）pt＞Qs，max.核A1与核A2都处于不饱和区.通过分区，将式（7）代入式（6）得到：

文献［9－10］认为，胶子的分布直接决定末态带电粒子数的分布，但是在与实验比较时发现在偏离中心区的大快度区域，由（8）的计算结果与实验值有差异.本文认为末态粒子的时空演化对粒子产生结果会有一定的影响.本文将采用流体力学的时空演化来描述演化特征，并将胶子饱和所得到的胶子分布作为流体演化的初始条件.近几年，笔者对相对论重离子碰撞的集体运动流体运动特性很关注［11－16］，讨论了一些实验结果.

在极端相对论能量，两个相向运动的核会发生洛伦兹收缩［17］.碰撞后的瞬间，它们会经历量子涨落（τ～（0－0.1）fm／c）和密度涨落、热化（τ～（0.1－1）fm／c）过程.对于相对论重离子碰撞，由于洛伦兹收缩效应，两个核收缩成薄板，流体在碰撞轴附近沿纵向运动.采用Bjorken假设［17］，认为y＝ηs，y 为能量动量快度，ηs为空时快度（ηs＝），根据式（8）给出点（τ0，y）的胶子数密度［18］

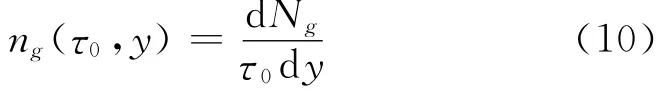
其中，τ0是碰撞后系统进入局域热平衡的时间，引入温度

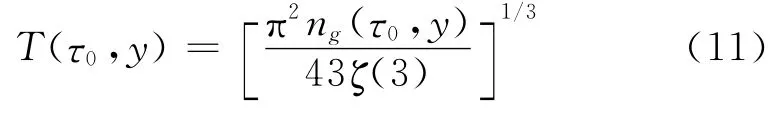
其中ζ（3）＝1.202 06.

Cooper－Frye理论中假定局域静止系中动量分布是各向同性的，并且可以用观测粒子的玻色分布或费米分布来描述［19－20］，不变单粒子在动量空间分布为

散射截面为

采用一个半径为R，长度为2η0的Bjorken柱，在没有横向流和温度变化不大的情况下，

所以末态带电粒子多重数分布为

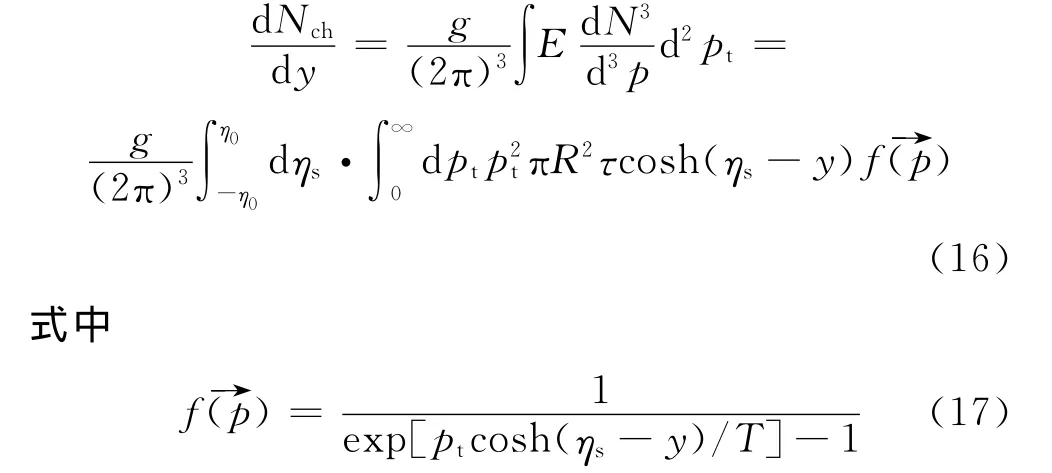
最后得到：

将式（11）和式（17）代入到式（16）中得到：

其中简并度g＝gg＋，胶子简并度gg＝8×2，（反）夸克简并度gq＝＝NcNsNf，色数 Nc＝3，自旋数Ns＝2，味数Nf＝3.

采用了以下代换：

2 高能重离子碰撞快度分布随中心度关系

高能重离子碰撞的中心区域带电强子多重数关系研究是一个重要研究课题.与核子－核子碰撞不同，核－核碰撞的多重数分布的中心度关系研究是深入了解核－核碰撞的一个重要课题，它可以帮助深入研究核－核碰撞一些特征.实验给出的赝快度分布与快度分布有一定的关系［21］，

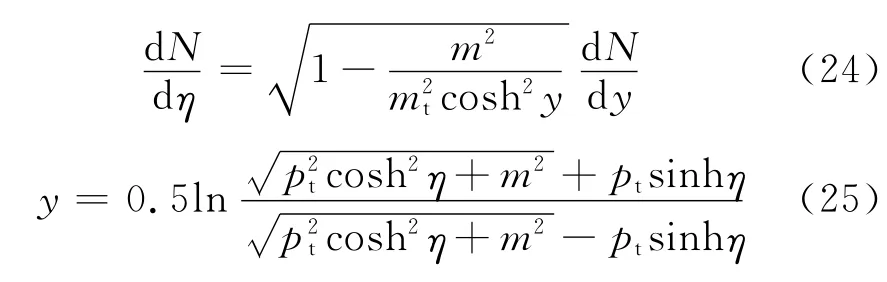
其中，dN／dy来自于式（23），从文献［9］，可以得到一些关系～N1／3part，m2～Qs，＝＋m2，pt＝Qs.

将胶子饱和理论和流体力学时空演化结合起来，拟合了RHIC能区的不同能量的末态带粒子分布随中心度变化关系.图3给出了中心赝快度区域（η＝0）RHIC能区Au＋Au碰撞质心系能量W 分别为19.6、62.4、130和200GeV的拟合结果，从图3可以看出：质心系能量越低，＜2／Npart且＞dNch／dη时随中心度变化越平坦，但随着质心系能量升高，越接近中心碰撞，每一对参加反应的核子对末态带电粒子多重数分布的贡献越来越大.还可以看出，在同一中心度情况下，随着碰撞质心系能量升高，每一对参加反应的核子对末态带电粒子多重数分布的贡献越来越大.同时，也拟合了中心赝快度区域（η＝0）RHIC能区Cu＋Cu碰撞质心系能量W 分别为22.4、62.4和200GeV的实验结果，图4也表现出类似于图3的分布特征.从图3和图4可以看出：把胶子饱和理论和流体力学时空演化结合起来所得到的理论结果可以很好解释RHIC能区的实验结果.

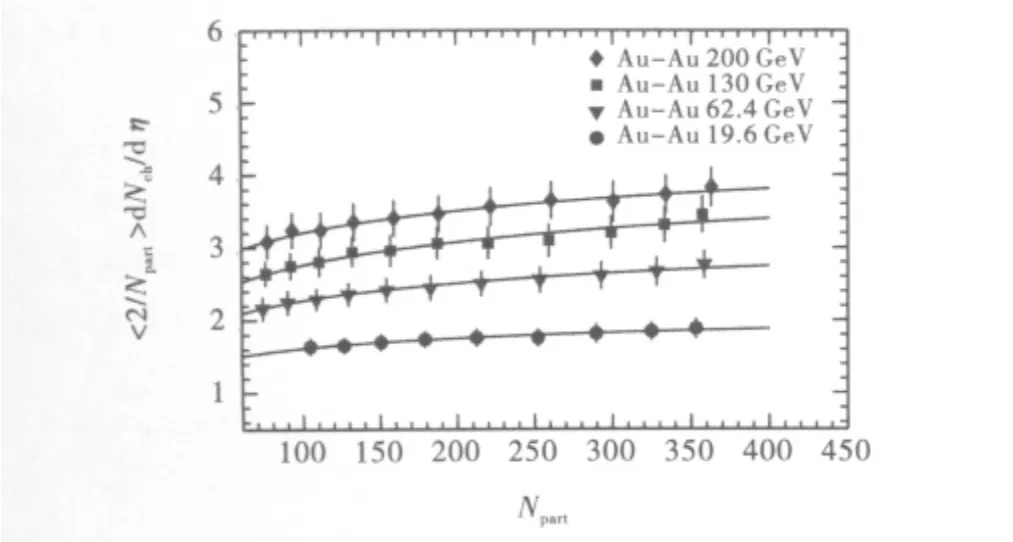
图3 RHIC能区中心赝快度区域（η＝0）Au＋Au碰撞质心系能量W 分别为19.6、62.4、130和200GeV的拟合结果，实验点来自于Phobos实验组［22］，实线是计算结果.

图4 RHIC能区中心赝快度区域（η＝0）Cu＋Cu碰撞质心系能量W 分别为22.4、62.4和200GeV的拟合结果，实验点来自于Phobos实验组［23］，实线是计算结果.

表1 Au＋Au碰撞系统中不同能量下流体力学演化参量与能量的关系

文中引入了Bjorken时空演化图像，2η0表示核－核碰撞洛伦兹收缩的色玻璃薄板的动力学范围.把Au＋Au碰撞系统中流体力学演化参量对能量的依赖关系进行拟合，得到（26）的关系曲线，其表达式为

从图5和上述表达式中可以看出η0随是递增的关系.

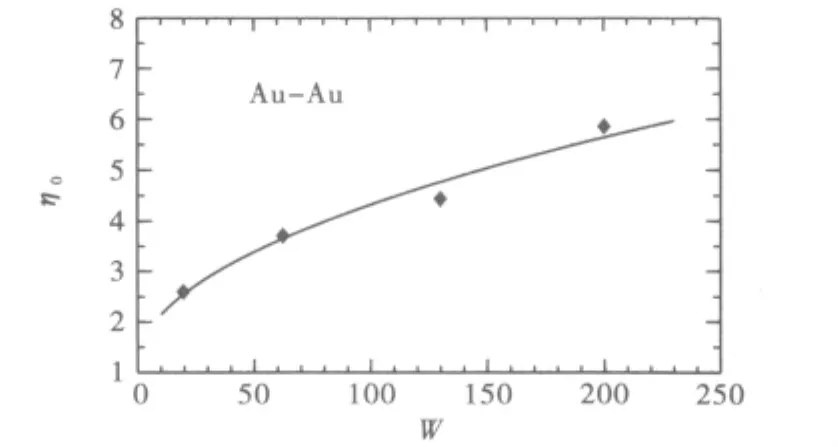
图5 Au＋Au碰撞统中流体力学演化参数对质心能量的依赖关系

填充点代表实验拟合时得到到参数，曲线代表参数拟合的曲线

3 结 论

将胶子饱和理论和流体力学时空演化结合起来，较好拟合了RHIC能区的不同能量的末态带粒子分布随中心度变化关系.发现：

（1）质心系能量越低，每一对参加反应的核子对末态带电粒子多重数分布的贡献随中心度变化越平坦，但随着质心系能量升高，越接近中心碰撞，每一对参加反应的核子对末态带电粒子多重数分布的贡献越来越大.

（2）在同一中心度情况下，随着碰撞质心系能量升高，每一对参加反应的核子对末态带电粒子多重数分布的贡献越来越大.

（3）在本文中，引入了Bjorken时空演化图像，2η0表示核－核碰撞洛伦兹收缩的色玻璃薄板的动力学范围.把Au＋Au碰撞系统中流体力学演化参量对能量的依赖关系进行拟合，得到了动力学范围随质心系能量关系η0＝0.319

［1］ Gribov L V，Levin E M，Ryskin M G.Semhard Processes in QCD［J］.Phys.Rep.，1983，100（1）.

［2］ Mueller A H，Qiu J.Gluon Recombination and Shadowing at Small Values of x.Nucl［J］.Phys.B，1986，268：427.

［3］ McLerran L，Venugopalan R.Compution Quark and Gluon Distribution Functions for Very Large Nuclei［J］.Phys.Rev.D，1994，49：2233.

［4］ Balitsky I.Operator Expansion for High－energy Scattering，Operator Expansion for High－energy Scattering［J］.Nucl.Phys.B，1996，463：99.

［5］ Jalilian－Marian J，Kovner A，Leonidov A，et al.The Wilson Renormalization Group for Low x Physics：Towards the High Density Regime［J］.Phys.Rev.D，1999，59：014014.

［6］ ZEUS Collaboration，Breitweg J，Chekanov S，et al.Measurement of Azimuthal Asymmetries in Deep Inelastic Scattering［J］.Phys.Lett.B.，2000，481：199.

［7］ ZEUS Collaboration，Breitweg J，Derrick M，et al.Measurement of the Diffractive Cross－section in Deep Inelastic Scattering Using ZEUS 1994data，Eur.Phys.J.C.，1999（6）：43.

［8］ ZEUS Collaboration，Breitweg J，Chekanov S，et al.ZEUS Results on the Measurement and Phenomenology of F（2）at Low x and Low Q＊＊2［J］.Eur.Phys.J.C.，1999（7）：609.

［9］ Dmitri Kharzeev，Eugene Levin.Manifestations of High Density QCD in the First RHIC Data［J］.Physical Letters B，2001，523：79－87.

［10］Dmitri Kharzeev，Evgene Levin，Marzia Nardi.Color Glass Condensate at the LHC：Hadron Multiplicities in pp，pA and AA Collisions［J］.Nuclear Physiscs A，2005，747：609－629.

［11］Feng S Q，Liu F，Liu L S.Thermal Equilibrium andNonuniform Longitudinal Flow in Relativistic Heavy ion Collisions［J］.Phys.Rev.C，2000，63：014901.

［12］Feng S Q，Yuan X B，Shi Y F.Collective Flow Distributions and Nuclear Stopping in Heavy－ion Collisions at AGS，SPS and RHIC［J］.Mod.Phys.Lett.A，2006，21：663.

［13］Feng S Q，Xiong W.Thermalization Component Model of Multiplicity Distributions of Charged Hadrons Measured at BNL （ENNlab＝2－11.6GeV），at CERN（ENNlab＝20－200GeV），and at BNL （√sNN＝19.6－200GeV）［J］.Phys.Rev.C，77，044906（2008）.

［14］Feng S Q，Yuan X B.The Feature Study on the and Proton Rapidity Distributions at AGS，SPS and RHIC［J］.Sci.China Ser.G 52，198（2009）.

［15］Cai X，Feng S Q，Li Y D，et al.Geometrical Description for the Negative Correlation Between Forward and Transverse Energies in Ultrarelativistic Heavy－ion Collisions［J］.Phys.Rev.C 51，3336（1995）.

［16］Feng S Q，Zhong Y.Baryon Production and Collective Flow in Relativistic Heavy－ion Collisions in the AGS，SPS，RHIC，and LHC energy Regions（GeV to 5.5 TeV）［J］.Phys.Rev.C83，034908（2011）.

［17］Bjorken J D.Highly Relativistic Nucleus－nucleus Collisions：The Central Rapidity Region［J］.Physical Review D 27，140（1983）.

［18］Tetsufumi Hirano，Yasushi Nara.Hydrodynamic Afterburner for the Color Glass Condensate and the Parton Energy Loss Hydrodynamic Afterburner for the Color Glass Condensate and the Parton Energy Loss［J］.Nucl.Phys.A743：305－328，2004.

［19］Fred Cooper，Graham Frye.Single－particle Distribution in the Hydrodynamic and Statistical Thermodynamic Models of Multiparticle Production［J］.Physical Review D 10，186－189（1974）.

［20］Phenix Collaboration.Systematic Studies of the Centrality and Dependence of the dET／dηand dNch／dηin Heavy ion Collisions at Midrapidity［J］.Physical Review C 71，034908（2005）.

［21］黄卓然，张卫宁，译.高能重离子碰撞导论［M］.哈尔滨：哈尔滨工业大学出版社，2002.

［22］Phobos Collaboration.Charged－particle Pseudorapidity Distributions in Au＋Au Collisions at＝62.4GeV［J］.Phys.Rev.C74，021901（2006）.

［23］Phobos Collaboration.Charged－particle Multiplicity and Pseudorapidity Distributions Measured with the PHOBOS Detector in Au＋Au，Cu＋Cu，d＋Au，and p＋p Collisions at Ultrarelativistic Energies［J］.Phys.ReV.C83 024913（2011）.