多学科优化设计在柴油机设计上的应用

徐 翔 周瑞平 汪萌生

（1.三峡大学 机械与材料学院，湖北 宜昌 443002；2.武汉理工大学 能源与动力工程学院，武汉 430063）

柴油机设计是典型的复杂机电系统设计，其涵盖了流体力学、热力分析、燃烧学、结构强度、振动力学、物理化学等多个学科的计算分析，而且各学科之间又相互影响，相互制约，有着复杂的耦合关系.柴油机的“传统设计”主要采用“设计－试验－修改设计－再试验”这种多次反复的方法，一个型号发动机的开发一般需要10年的时间，耗费巨大.

多学科优化设计方法 MDO（Multi－disciplinary Design Optimization）是从20世纪80年代由飞行器设计领域兴起的一种分析和求解复杂工程系统的理论和方法.目前应用主要集中在航天领域的飞行器设计，很少拓展到交叉学科较多的柴油机系统设计领域.NASA给多学科设计优化方法（MDO）的定义是［1］:在系统设计过程中，必须考虑其所涉及的几门学科之间的互相影响和耦合作用，并且设计者应同时在多门学科中进行设计，以使系统综合性能达到最优的一种设计方法.多学科优化方法集成了多种设计和分析工具，使产品设计从孤立的、串行的过程成为并行的、协同的过程，把产品设计的焦点从单独的部件级转移到产品系统级整体性能优化，可以显著提高产品设计的效率［2－3］.

MDO思想符合柴油机设计的要求，与现代系统论的整体优化思想一致.柴油机的总体综合设计需要设计的变量很多，包括机体、曲轴、缸盖、活塞、连杆、缸套、轴承、配气机构、燃油喷射系统和热力过程等多个组成部分和学科的相关参数，同时还要综合分析经济性、技术、性能、可靠性等指标.本文以MDO理论为指导，在柴油机设计中进行多学科优化设计方法的研究.

1 协调优化算法（CO）

协调优化算法是一种针对复杂系统设计问题的分布式、多级的多学科优化方法，对每个子空间不仅进行分析，而且进行设计优化.它将复杂的系统设计问题分解为一个系统级和并行的几个学科（子系统）级问题，并通过系统级约束条件来协调各学科之间的共享设计变量和耦合状态变量.其主要思想是:在优化时可以暂时不考虑其它学科的影响，只需要满足本学科的约束，学科级优化的目标是使该学科优化结果与系统级优化提供给该学科的目标值的差异达到最小，而各个学科级优化结果的不一致性由系统级优化来协调，通过系统级优化和学科级优化之间多次迭代，最终得到一个符合学科间一致性要求的系统最优化设计方案［4］.

协同优化方法采用系统层和学科层两层结构来求解MDO问题.其中系统层设计为系统优化器，针对系统的目标函数，对系统设计变量和耦合变量进行设计，以作为各学科设计的目标值，同时要求满足各学科的一致性约束和系统层约束.

系统层的优化问题可定义为:

学科层设计为各学科优化器，针对各学科的设计、分析参数与相应系统设计目标值之间的一致性函数，设计本学科设计变量及相关的耦合变量和系统变量输入值，同时满足本学科的设计约束.在系统层设计中，学科设计变量作为常数；在学科层设计中，系统层的设计结果作为常数.

其算法框图如图1所示，该图显示了协同优化求解思路:系统层负责规划协调，指挥优化的大方向，相容性约束负责进行间接解耦，子系统层主要负责相容性优化，研究优化的可行性.

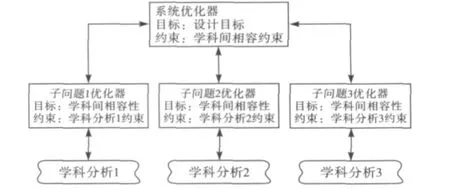
图1 CO优化算法结构图

从CO的寻优过程可以看出，这种算法结构与复杂工程设计的组织相当吻合，系统层代表总体组，学科级优化代表了实际设计过程中的某一学科领域，并且每个子系统优化时不受其他子系统的影响，学科专家可以灵活采用适合本学科的分析方法和优化方法进行学科设计，具有高度设计自由度.此外，CO将多学科优化任务进行分解，各子系统负责本学科相关设计变量的优化，系统级负责学科间不一致性的协调优化，所以，CO具有很强的工程适用性，能够处理大规模多学科优化问题.

2 柴油机设计系统的分层和建模

2.1 系统总体综合设计的多学科分析

建立系统模型是多学科设计优化的前提，按MDO思路和采用层次分解的方法将柴油机系统分解为两个基本层次:最顶层系统级优化指标为经济指标、技术性能指标、可靠性和使用寿命；根据柴油机的用途、设计功率及转速等参数，确定柴油机的总体参数.首先根据用途及功率确定柴油机是四冲程还是二冲程，是否采用增压，确定平均有效压力的范围，然后确定缸径及转速和气缸数.

分系统级（学科级）主要有柴油机结构尺寸设计、热力学经济性分析、动力学计算、排放分析和预估、振动和噪声分析和预估、可靠性和使用寿命分析6个学科，各学科设计和耦合内容如图2所示.

柴油机结构尺寸设计（学科1）:在满足柴油机功能和强度的前提下，合理配置各零部件设计参数，尽量减小结构的外形尺寸和重量，力求比质量最小，为其他学科分析提供结构尺寸模型.

热力学经济性分析（学科2）:柴油机工作过程的热力模拟计算是方案设计阶段获知结构参数与性能指标关联度的主要依据.凭借对柴油机工作过程的建模和数值计算，可以确定实现的性能指标最优的热工参数匹配，也可通过它来获取一些参数作为排放和其他计算的输入边界条件.

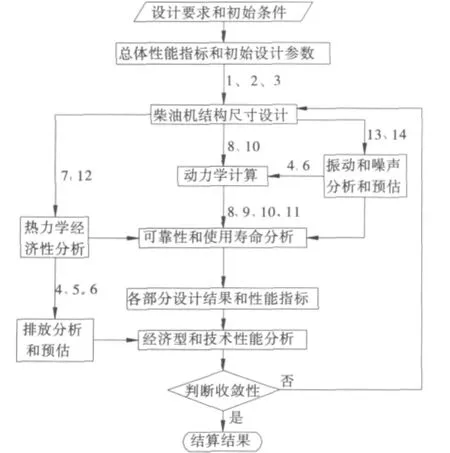
图2 柴油机多学科优化设计模型

动力学计算（学科3）:主要是通过曲柄－连杆机构以及整个轴系的运动学和动力分析，对各运动零部件和飞轮惯性质量结构尺寸参数的调整，改善轴系的平衡性能.另外还包括配气机构的结构设计和动力学分析，进行活塞、连杆和曲轴以及轴承等各个重要零部件的结构设计，在机械负荷和热负荷作用下零部件的强度计算分析，并为整机的振动噪声分析提供载荷和边界条件等.

排放分析和预估（学科4）:根据柴油机燃烧过程数值模拟计算，对有害排放物预估，优化配置压缩比、进气温度、进气压力、过量空气系数等参数以满足使用要求和规定的限制.

振动和噪声分析和预估（学科5）:主要根据柴油机各机构动力学计学分析提供的参数和边界条件，对轴系振动进行计算分析，再对整机的振动噪声进行分析和预测，来优化柴油机结构尺寸参数.

可靠性和使用寿命分析（学科6）:对柴油机关键零部件进行可靠性分析，依据主要零部件的磨损量预估使用寿命，通过优化设计参数，减少磨损量和变形量，以提高设备可靠性和延长的大修期.

学科间的耦合参数:（1）气缸直径，（2）活塞行程，（3）压缩比，（4）气体平均有效压力，（5）排气温度参数，（6）缸内初始工作状态参数，（7）燃烧室形状，（8）活塞曲轴连杆机构外形结构尺寸，（9）活塞曲轴连杆机构动力学参数，（10）配气机构外形尺寸，（11）配气机构动力学参数，（12）喷油提前角，（13）轴系振动参数，（14）整机振动参数等.

2.2 系统多学科数学模型的建立

下面给出一个通用的柴油机系统设计的MDO分析模型.

系统层的设计变量有:气缸直径D，活塞行程S，平均有效压力Pe，连杆中心矩L，转速n.系统层变量集:X0＝ ｛D，S，Pe，L，n｝.

学科1的设计变量集为X1，它含有气缸直径、气缸中心距、活塞行程、连杆长度、缸头的结构参数和机体结构参数等设计变量；学科2的设计变量集为X2，它含有气缸直径、活塞行程、理论平均气体压力，排气温度，有效功率，热效率，燃油消耗率，学科3的设计变量集为X3，它含有曲轴结构参数，活塞结构参数，连杆结构参数，曲轴轴承结构参数，飞轮结构参数，凸轮和挺杆结构参数等；学科4的设计变量集为X4，它含有喷油提前角，燃烧室形状参数，进气和排气道形状参数，学科5的设计变量集为X5，它含有轴系振动参数，整机振动参数等；学科6的设计变量集为X6，它含有活塞环结构参数，曲轴结构参数等.

在总体综合设计中，经济性E（平均有效压力、有效燃油消耗率）、技术性能M（比质量、振动噪声值、排放指标）和可靠性F为优化设计的目标函数，并假设各学科设计的约束与状态函数:

系统层的设计约束与状态函数为Gs和Hs，数学模型为:

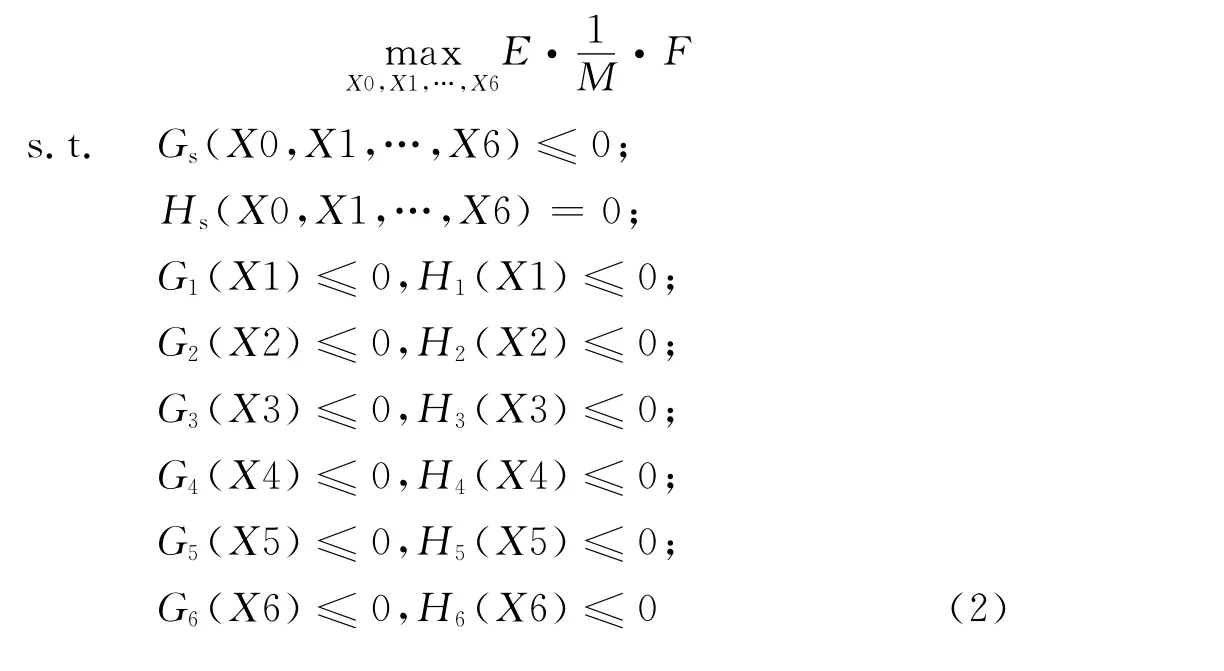
3 柴油机系统CO方法

根据上面的协调优化法（CO）原理，要求对系统设计变量和耦合变量进行设计，作为各学科设计的目标值，同时要求满足各学科的一致性约束和系统层约束；学科层设计为各学科优化器，针对各学科的耦合变量在系统层进行协调，再将协调值返回给各个子学科［5］.则数学模型变为:

式中，C1，C2，…，C6为各学科设计参数与系统目标值之间的一致性函数.

学科i的数学模型为［6］:

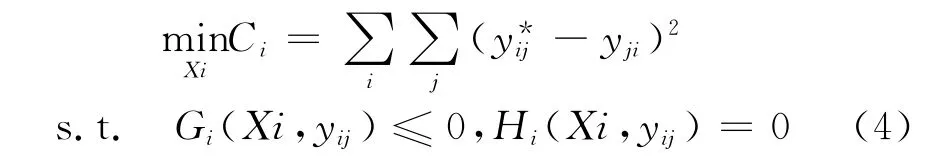
式中，yji为第i学科中第j个设计变量；为系统层与第i学科中第j个设计变量相对应的辅助变量.

CO协调优化模型如图3所示.

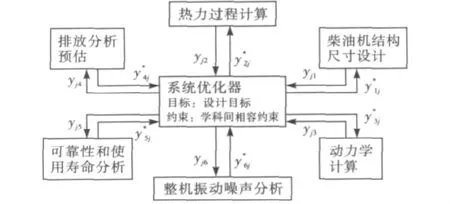
图3 协调优化计算模型

4 实际应用设计

根据上述的建模思路和优化方法对某型号的柴油机进行优化计算，考虑计算复杂性和优化计算过程需要的时间问题，将优化计算的过程进行简化，在额定功率和转速下，将其中的一些设计变量缸径、气缸数和气缸中心距作为常量，系统优化设计变量为活塞行程，连杆中心距，排气温度，平均有效压力，燃烧室形状参数，喷油提前角等，经济性、技术性能和可靠性的权重比都为1，各个学科分别建立数学模型，相关计算公式可参见文献［7］，进行数值计算和仿真，学科间的耦合变量通过系统层协调，则最后的计算结果见表1.由表1可见，优化设计后柴油机在经济型，可靠性和技术性能方面都有不同程度的提高.

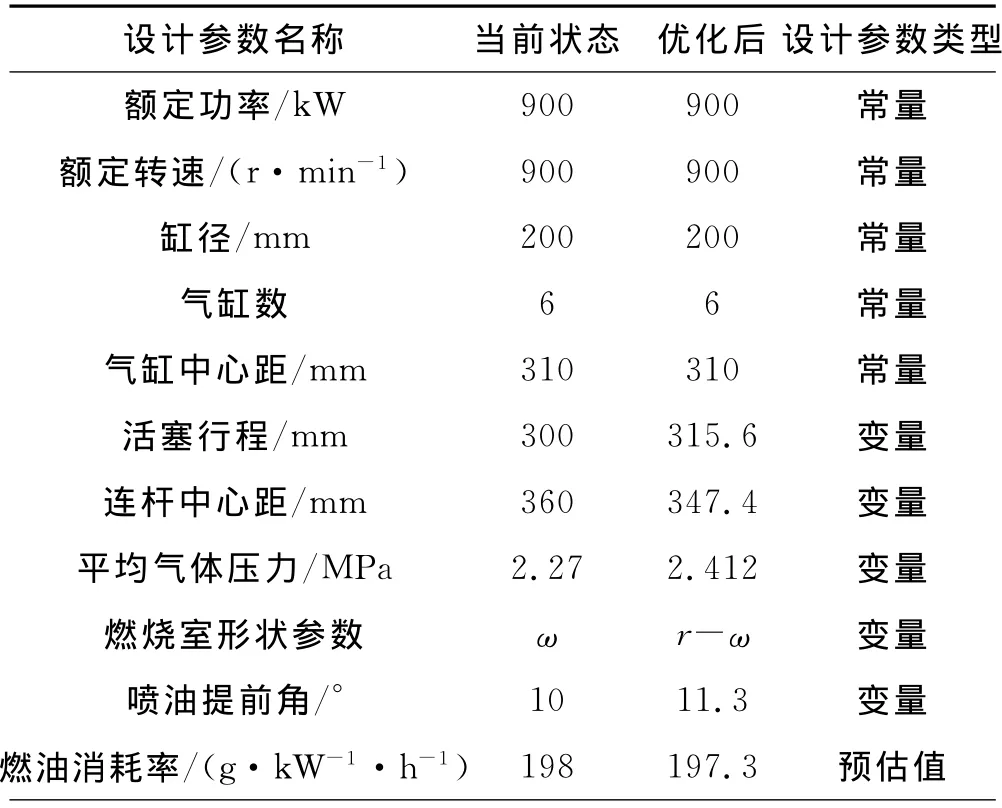
表1 优化计算结果

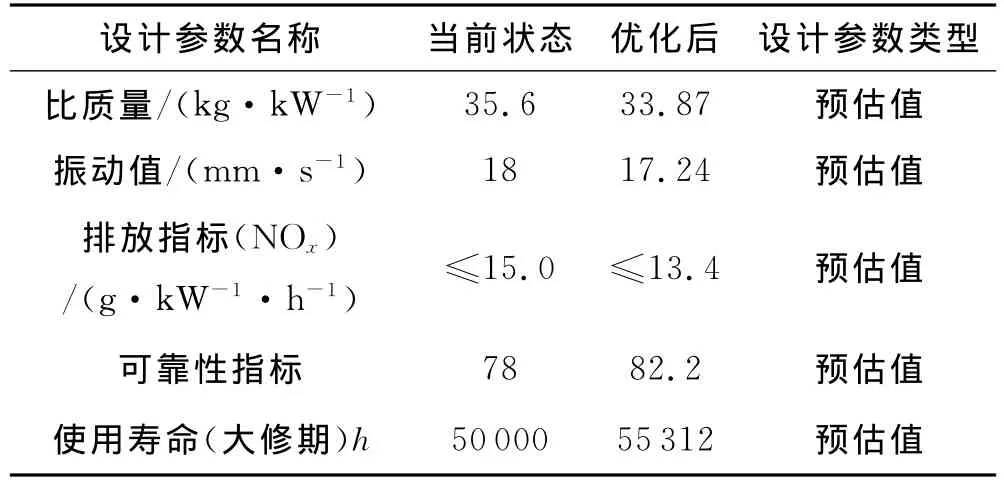
续表1 优化计算结果

5 结 论

传统的柴油机设计方法中，各个部分和各个学科独立进行设计，很少考虑相互间的耦合关系.本文在总体综合设计方法中使用了多学科协调设计优化方法，对其中的耦合关系进行了重点分析，并在目标函数中综合考虑了经济型、技术性能和可靠性等指标，通过设计参数的优化配置，使得系统的综合性能得到有效的提高.多学科设计优化的理论和方法在柴油机设计领域的应用还未见有相关的论文和报告.本文运用多学科设计优化方法对柴油机总体综合设计的建模和优化方法进行研究，既是对多学科设计优化方法一种新的尝试，也是对其应用领域的拓广，同时也需要对该方法的应用作进一步的深化与完善.

［1］J.Sobieszezanski－Sobieski，Haftka T.Mult－disciplinary Aero Space Design Optimization:Survey of Recent Developments［R］.AIAA 9620711，Nevada:AIAA，1996.

［2］陈柏鸿，肖人彬.复杂产品协同优化设计中耦合因素的研究［J］.机械工程学报，2001，37（1）:9－13.

［3］陈树勋.基于人工智能的机械系统多学科优化探讨［J］.现代工程制造，2004（5）:11－13.

［4］王振国，陈小前，罗文彩，等.飞行器多学科设计优化理论与应用研究［M］.北京:国防工业出版社，2006.

［5］卜广志，张宇文.使用多学科设计优化方法对鱼雷总体综合设计的建模思路研究［J］.兵工学报，2005（2）:163－168.

［6］操安喜，赵 敏，刘 蔚，等.Application of Multidisciplinary Design Optimization in the Conceptual Design of a Submarine［J］.船舶力学，2007（3）:73－77.

［7］周龙保.内燃机学（第2版）［M］.北京:机械工业出版社，2005.