一类二阶变系数非线性微分方程的通解及应用

冯录祥

（宝鸡文理学院 数学系，陕西 宝鸡 721013）

二阶变系数线性微分方程在常微分方程理论中占有重要地位，在工程技术及力学和物理学中都有十分广泛的应用.关于它的通解结构已有十分完美的结论，但其求解却无一般方法.因此，二阶变系数线性微分方程的求解成为常微分方程研究的热点问题之一.一般地，二阶变系数线性微分方程通常是不可积的，但是人们在一些特殊情形下仍然获得了一些可积性结果［1－8］.本文将研究一类二阶变系数非线性微分方程的可积性，在n＝0时得到一系列可积的二阶变系数非齐次线性微分方程及其通解公式，进一步丰富了二阶变系数非齐次线性微分方程的可积理论.特别说明，本文中“∫”表示被积函数的一个确定的原函数.

1 主要结果及证明

定理 设∃λ（x）∈C′，使得二阶变系数非线性微分方程（1）满足

则方程（1）可积，且

（i）当n＝0时，通解为

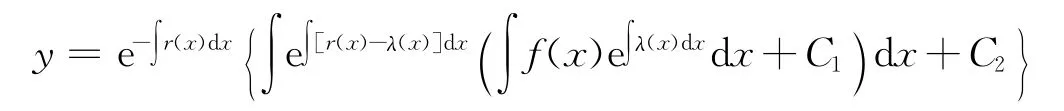
（ii）当n＝1时，通解为

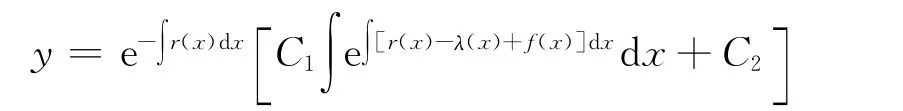
（iii）当n≠0，1时，通解为

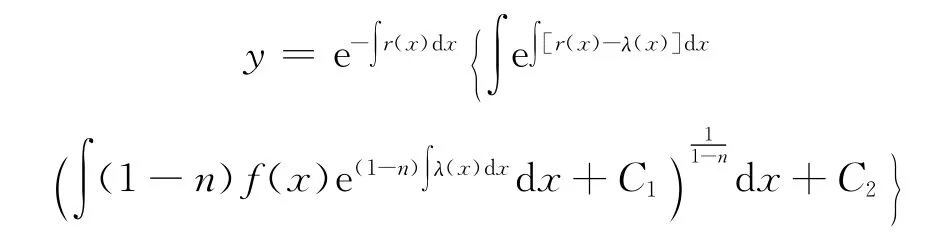
证明：由于p（x）＝r（x）＋λ（x），q（x）＝r′（x）＋r（x）λ（x），则方程（1）变为

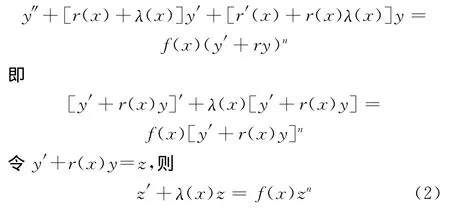
（i）当n＝0时，（2）是一阶线性微分方程z′＋λ（x）z＝f（x），其通解为

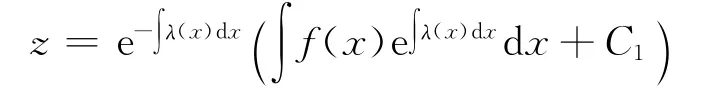
把上式代入y′＋r（x）y＝z，则原方程（1）变为

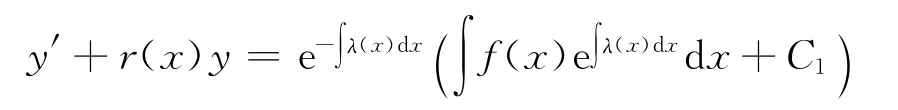
于是可积，且其通解为

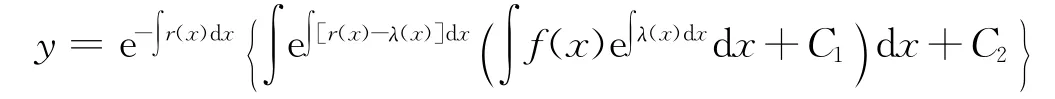
（ii）当n＝1时，（2）为z′＋［λ（x）－f（x）］z＝0，这是变量分离方程，其通解为z＝C1e－∫［λ（x）－f（x）］dx，把它代入y′＋r（x）y＝z，则原方程（1）变为

于是可积，且其通解为

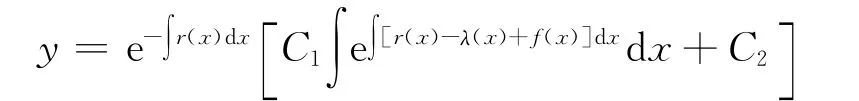
（iii）当n≠0，1时，方程（2）为贝努利方程，其通解为

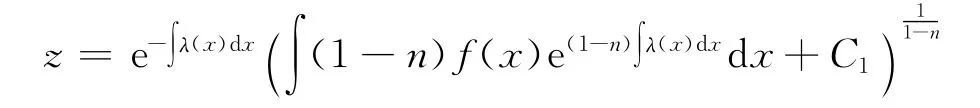
把其代入y′＋r（x）y＝z，则原方程（1）变为

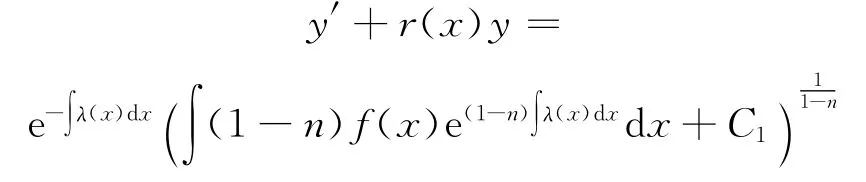
于是可积，且其通解为

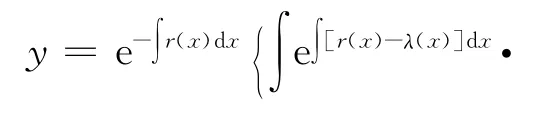
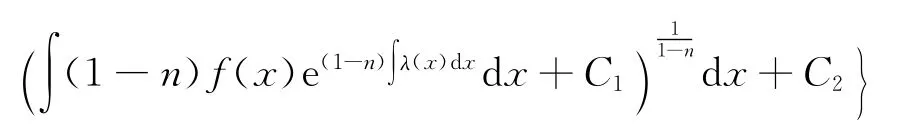
推论1 设a是常数，λ（x）∈C′，则二阶变系数非齐次线性微分方程

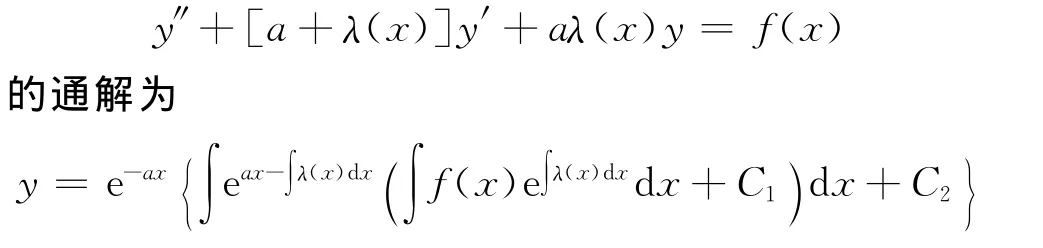
证明：在定理（i）中取r＝a为常数，立得.

推论2 设a是常数，则二阶变系数非齐次线性微分方程

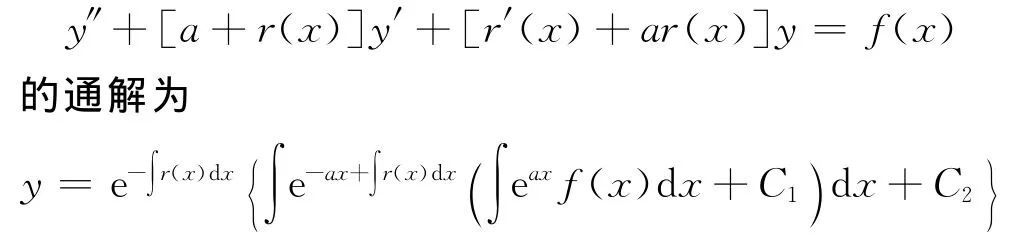
证明：在定理（i）中取，λ（x）＝a为常数，立得.

推论3 二阶变系数非齐次线性微分方程

证明：在定理（i）中取r（x）＝λ（x），立得.

推论4 二阶变系数非齐次线性微分方程

证明：在定理中取λ（x）＝－r（x），立得.

2 应 用

例1 解微分方程：

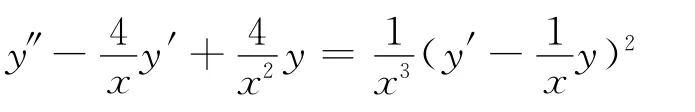
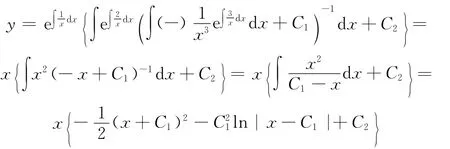
例2 解微分方程：

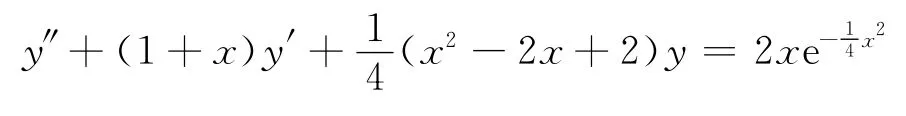
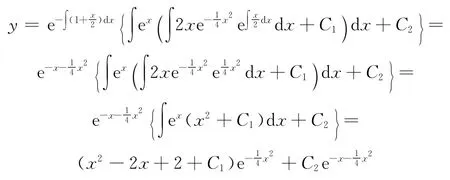
例3 解微分方程：

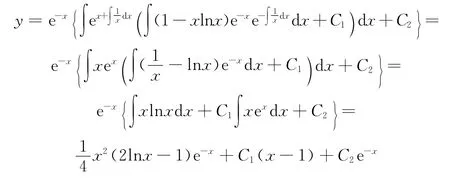
例4 解微分方程：

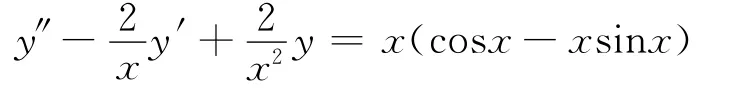
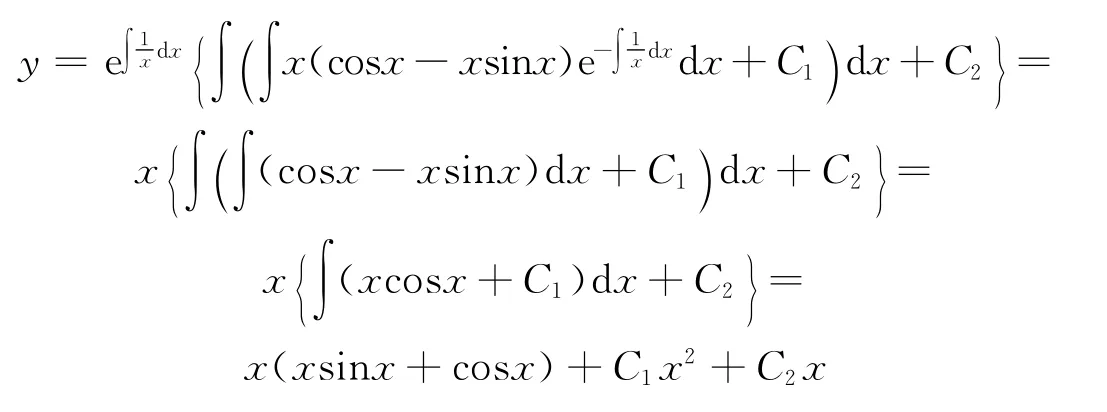
［1］ 孙晓莉.二阶变系数线性微分方程的几个可积类型［J］.大学数学，2010，26（6）：191－195.

［2］ 敏志奇.一类二阶变系数线性微分方程的可积定理及应用［J］.甘肃高师学刊，2010，15（2）：6－7.

［3］ 敏志奇.一类变系数微分方程通解公式的求法［J］.高等数学研究，2005，18（3）：16－17.

［4］ 伍锦棠.二阶线性微分方程的可积性判据［J］.大学数学，2010，26（4）：165－168.

［5］ 何基好.一类二阶变系数线性微分方程通解的解法［J］.贵州大学学报，2009，26（6）：1－3.

［6］ 李 高.关于二阶变系数线性微分方程求解法的研究［J］.河北北方学院学报，2010，26（6）：12－14.

［7］ 胡劲松.一种二阶变系数线性微分方程的求解方法［J］.重庆工商大学学报，2005，22（3）：96－98.

［8］ 李鸿祥.一类二阶变系数线性微分方程的另二种解法［J］.高等数学研究，2003，6（2）：18－21.