基于维纳滤波图像复原的设计与实现

魏 扬

（四川理工学院计算机学院，四川 自贡 643000）

基于维纳滤波图像复原的设计与实现

魏 扬

（四川理工学院计算机学院，四川 自贡 643000）

像复原的目的是从退化图像中重建原始图像，改善退化图像的视觉质量。维纳滤波能够较好地进行图像恢复。【关键词】维纳滤波；图像恢复；图象退化模型

图像在形成、传输和记录过程中，由于受多种原因的影响，图像的质量会有所下降，典型表现为图像模糊、失真、有噪声等，这一过程称为图像的退化。引起图像退化的原因有很多，比如大气湍流效应、传感器特性的非线性、光学系统的像差、成像设备与物体之间的相对运动等。

1 图像退化模型

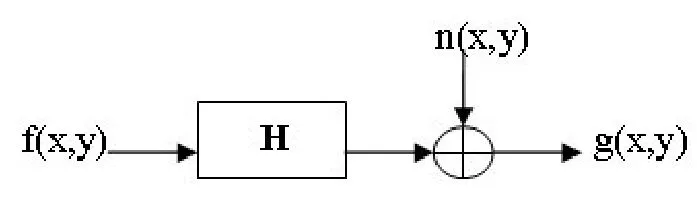
图1 图像退化模型

图像复原试图利用退化现象的某种先验知识，即退化模型。对已经退化了的图像加以重建和复原。但是实现图像复原需要弄清楚图像退化的原因，建立相对应的数学模型，并沿着图像质量降低的逆过程至原始图像进行复原。图1为简单通用的图像退化模型，原始图像f(x,y)是由于通过了一个系统 H和外来的加性噪声 n(x,y), 而使其退化为一幅图像g(x,y)。表现为数学公式为

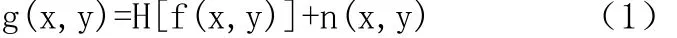
图像复原可以看成一个估计过程，因为加性噪声n(x,y)是一种有统计性质的信息，如果估计出系统 H，那么有给定的退化图像g(x,y)可以接近地恢复f(x,y)。由此可见，图像复原的关键是确定系统H。一般而言，H是由某些原件或部件以一定方式构造而成的整体，是输入型号和输出信号之间的联系。

2 线性复原算法

图像复原的主要目的是在假设具备退化图像 g(x,y)及H(x,y)的某些只是的前提下，估计出原始图像f(x,y)的估计

有约束维纳滤波：如果要求某种优化准则为最优的同时，还要考虑其他条件约束，这种复原方法有约束复原方法。图像恢复的原理：维纳滤波方法也就是最小二乘滤波，它是原

∧始图像f(x,y)及其恢复图像f(x,y)之间的均方误差最小的复原方法。

设原始图像为f(x,y)，退化图像为g(x,y),图像噪声为n(x,y)。他们之间的关系如下：

其中，f(x,y)、g(x,y)、n(x,y)是随即场，并假定噪声的统计特性已知。因此，在给定了 g(x,y),∧仍然不能精确求解f(x,y)，只能找出f(x,y)的一个估计值使得均方误差最小，即

∧

∧

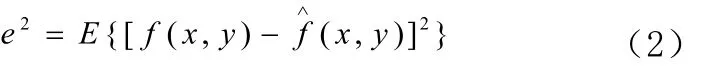
在总体建筑工程中，计算机的引用可以有效避免很多事故的发生，利用计算机编排的程序，可以快速检测建筑的各项数据以及对建筑的实际情况做具体研究。在建筑建设过程中，计算机对整体建筑系统的运作起着不小的作用。把建筑信息化，有利于建筑的整体规划，不妥的地方都可以直观地展现出来，并且在一些特定的地方，信息化的建筑还可以为工程师提供灵感，使建筑的综合性能得到提升。

其中f(x,y)是给定g(x,y)对f(x,y)的最小二乘方估计。对于上式通过傅立叶变化转换为频域 的计算，则误差函数的最小值在频域用下列表达式计算。

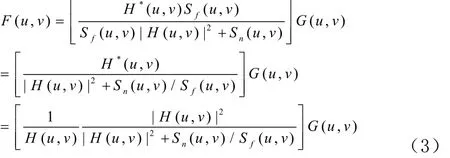
式(3)中H(u,v)为点扩散函数的傅里叶变换；H*(u,v)是H(u,v)的复共轭，|H(u,v)|2= H*(u,v)H(u,v); Sn(u,v)为噪声的功率谱；Sf(u,v)为未退化图像的功率谱。对式(3)进行傅立叶反变换可得

2.1 算法描述

关于维纳滤波方法的实现，首先仍要确定点扩散函数h，选取的h仍为

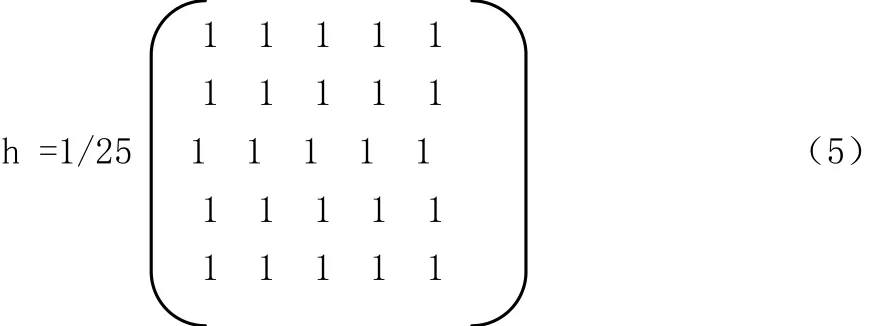
维纳滤波方法的实现步骤如下：

（1）对退化图像为g(x,y)及点扩散函数h(x,y)进行傅里叶变换，得到G(u,v)和H(u,v)；

2.2 VC编程实现维纳滤波方法的主要代码

}}

Fourn(fftSrc,nn,2,-1);//对结构图像进行反FFT//确定归一化因子for(){for(){

ffrSrc[(2*lLineByres)*j+2*i+1]=sqrt(fftSrc[(2*l LineByres)*j+2*i+1]*fftSrc[(2*lLineBytes)*j+2*i+1]+fftSrc[(2*lLineBytes)*j+2*i+2]*fftSrc[(2*lLineBytes)*j+2*i+2]);

if(MaxNum< fftSrc[(2*lLineBytes)*j+2*i+1])MaxNum = fftSrc[(2*lLineBytes)*j+2*i+1];}}

//转换为图像

for(;;)

{

for(;;)

{lpSrc=(char *)lpDIBBits + lLineButes * j + i;* lpSrc =(unsigned char )(fftSrc[(2*lLineBytes)*j+2*i+1]*255.0/ MaxNum);

}}}

上述代码实现了维纳滤波对图像的复原功能，对此进行了测试。维纳滤波方法能够有效地提高模糊图像的清晰度，而且复原后的图像没有出现白色斑点，结果好于原图片，对比结果如图a、b所示。

a 加噪的图像

b 维纳滤波复原后的图像

3 结论

在对图像缺乏足够的先验知识时，可以利用已有的知识和经验对模糊或噪声等退化过程做数学建模进行图像恢复。维纳滤波是假设图像信号可以近似看成平稳随即过程的前提下，按照使输入图像和恢复图像之间的均方误差达到最小的准则函数来实现图像恢复的方法。

[1] 刘海波,沈晶 郭耸.Visual C++数字图像处理技术详解[M].北京:机械工业出版社,2010.

[2] MariaPerrou赖剑煌译.数字图像处理疑难解析[M].北京:机械工业出版社,2005.

[3] 阮秋琦.实用数字图像处理[M].北京:电子工业出版社,2001.

The Design and Implementation of image restoration Based on wiener filter

WeiYang
(Sichuan University of Science& engineering,school of Computer Science,Zigong 643000)

The purpose of the image restoration of degraded image reconstruction from the original image, improve degradation image visual quality. Wiener filtering can well for image restoration.

wiener filtering、mage restoration、mage degradation model

TN911.73

A

1008-1151(2011)08-0052-03

2011-05-14

魏扬（1983－），男，四川自贡人，四川理工学院计算机学院教师，研究方向为计算机软件工程。