一级倒立摆仿真模型的建立
翟龙余
(江苏财经职业技术学院,江苏 淮安 223001)
一级倒立摆仿真模型的建立
翟龙余
(江苏财经职业技术学院,江苏 淮安 223001)
针对一级倒立摆系统,首先利用牛顿力学的知识建立了数学模型,然后利用Simulink及其封装功能建立了倒立摆系统的仿真模型,使模型更具灵活性,给仿真带来很大方便。
倒立摆;数学模型;仿真模型
倒立摆系统是研究控制理论的一种典型实验装置,具有成本低廉,结构简单,物理参数和结构易于调整的优点,是一个具有高阶次、不稳定、多变量、非线性和强藕合特性的不稳定系统。在控制过程中,它能有效地反映诸如可镇定性、鲁棒性、随动性以及跟踪等许多控制中的关键问题,是检验各种控制理论的理想模型。本文以一级倒立摆为例,首先建立了倒立摆系统的数学模型,最终利用simulink建立其仿真模型。
1 一级倒立摆系统的数学模型
经过小心的假设忽略掉一些次要的因素,如忽略了空气阻力、系统内部的摩擦,不考虑构件的变形,则可以将直线一级倒立摆系统抽象成小车和匀质杆组成的系统,如图1所示。这是一个典型的运动刚体系统,可以在惯性坐标系内应用经典牛顿力学理论建立系统的动力学方程。[1]
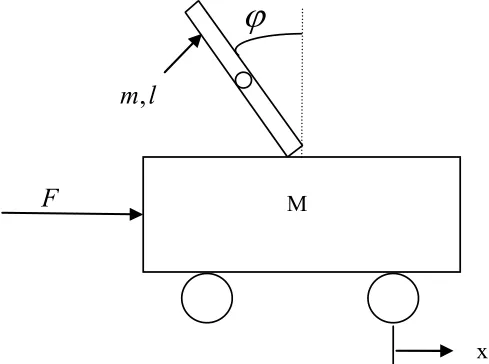
图1 倒立摆系统
各参数符号含义如下:

符号 含义单位M 小车质量kg m 摆杆质量kg b 小车摩擦系数N/m/sec l 摆杆转动轴心到杆质心的长度 m I 摆杆转动惯量kg*m2 F 加在小车上的力N x 小车位置m摆杆与垂直向上方向的夹角 rad
图2是系统中小车和摆杆的受力分析图,其中,N 和P为小车与摆杆相互作用力的水平和垂直两个方向的分量。矢量正方向如图2所示。
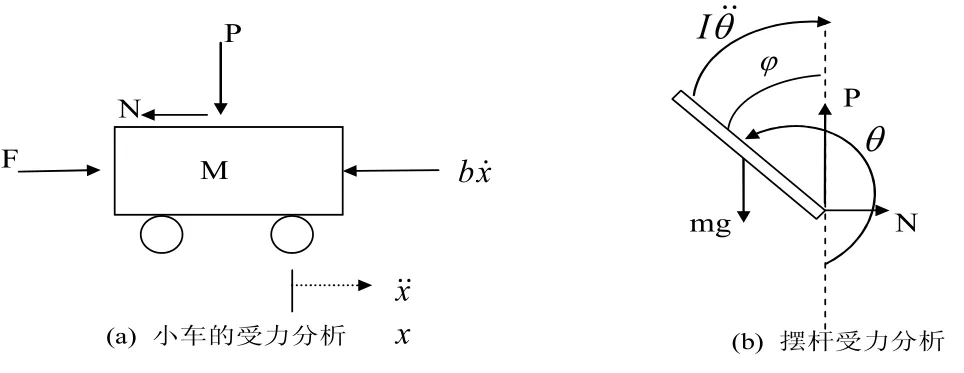
图2 小车与摆杆的受力分析
小车作平动,由小车的水平受力分析,可以得到以下方程:
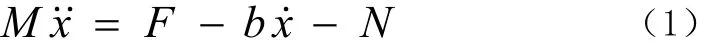
摆杆作平面运动,可分解为质心的平动和绕质心转动,由水平方向的受力分析,可以得到下式:
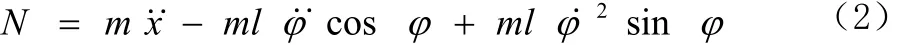
代入(1)式得:
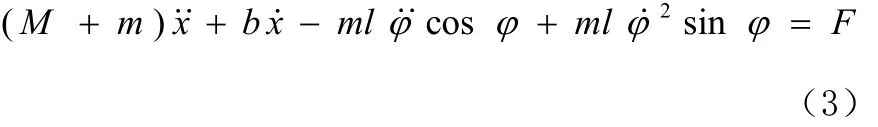
再由摆杆的垂直方向的受力分析,得到下式:
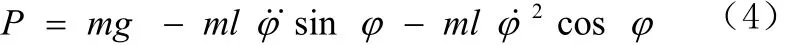
又由摆杆对质心的力矩平衡方程有:
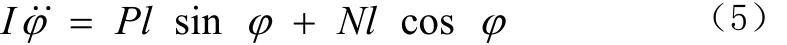
整理得:
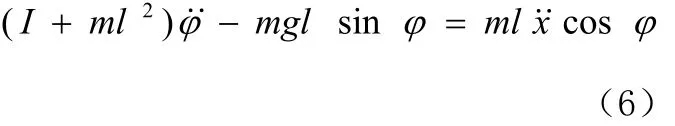
在 与 1(单位是弧度)相比很小,即 <<1时,则可以进行近似处理: cos ≈ 1,sin ≈ ˙≈0。用u来代表被控对象的输入力 F,线性化后得到两个运动方程如下:
可解得:
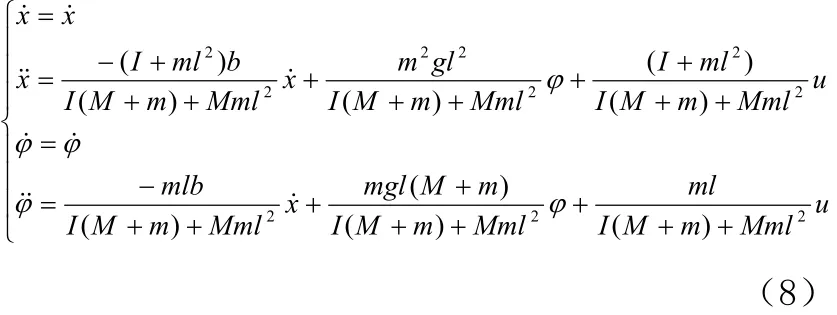
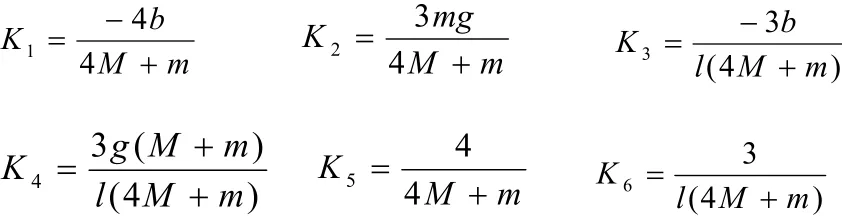
经整理后得到倒立摆的数学模型简化形式如下:
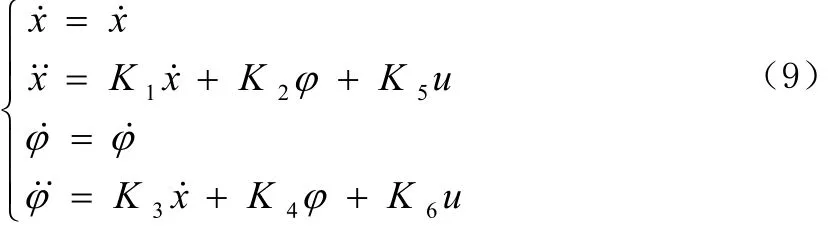
2 一级倒立摆系统的仿真模型
Simulink是Matlab最重要的组件之一,它提供一个动态系统建模、仿真和综合分析的集成环境。在该环境中,可以构造出复杂的仿真模型,下文根据倒立摆的数学模型,利用 Simulink的封装功能,构建了倒立摆系统仿真模型子系统。[2]
根据倒立摆的数学模型即表达式(9),在Matlab中,用Simulink构建一级倒立摆模块 SingleInvPend,具体步骤如下:
(1)双击Matlab图标,启动Matlab,在工具栏中双击Simulink图标启动Simulink 模块库浏览器窗口,然后再单击其工具栏中的新建(creat a new mode)图标,新建一个Simulink模型窗口。
(2)从Simulink模块库浏览器的菜单Simulink的子菜单端口和子系统模块(Port & Subsystems)下选中子系统Subsystem,并用左键拖入到新建的Simulink模型窗口中。左击系统框图下字符串“Subsystem”,删除后输入“SingleInvPend”,实现子系统的重新命名。结果如图3。
图3 SingleInvPend模块

图4 SingleInvPend模块
(3)双击图3中的SingleInvPend模块,从Port &Subsystems下在拖出三个输出模块out,把一个输入模块和四个输出模块分别重新命名为:u和 x 、x'、 a 、a',分别代表系统的输入向量u和输出向量 x、x˙、 、˙(Matlab中不支持公式编辑器和希腊字母)。结果如图4。
(4)双击SingleInvPend模块,然后从Simulink下子菜单“用户自定义函数模块”(User-Defined Functions)中拖出Fcn子模块,单击Fcn子模块下的Fcn,删除Fcn重新命名为K1;再双击Fcn子模块并将对话框中的“Expression”中的内容修改为:[ -4*b /(4*M +m1)]*u,然后按OK,这就定义好了K1。(说明:由于matlab子系统的变量名是不区分大小写,所以数学模型中的摆杆的质量m在matlab中用m1代替)
(5)重复步骤4)依次定义K2、K3、K4、K5、K6。
(6)在窗口中再加入四个积分模块和两个加法模块,双击四个积分模块,把“Initial condition”下的内容分别修改为“init_cond(1)、init_cond(2)、init_cond(3)、init_cond(4)”。它们表示倒立摆的系统的初始条件。
(7)把所有模块按公式(9)的运算关系连结起来,得到子系统的内部结构图,如图5所示。
(8)利用 Simulink的 Mask功能进行封装。右击SingleInvPend模块,选择Mask Subsystem(封装子系统)菜单,弹出子系统封装对话框,点击Parmeters标签,在参数对话框中,依次添加 init_ cond 、M、M1、l、b、g等各参数变量,结果如图6。
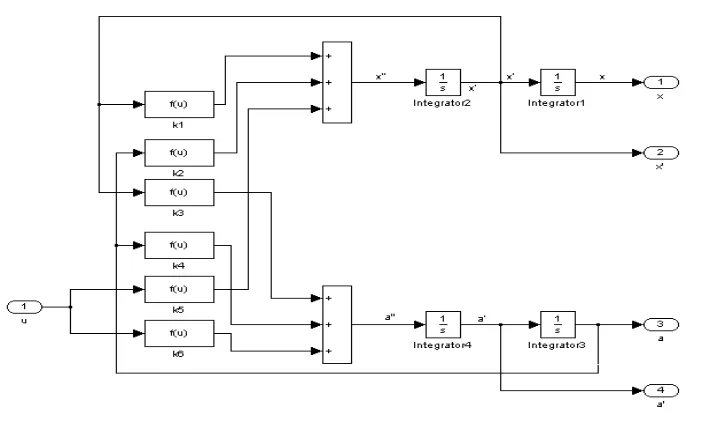
图5 子系统内部结构
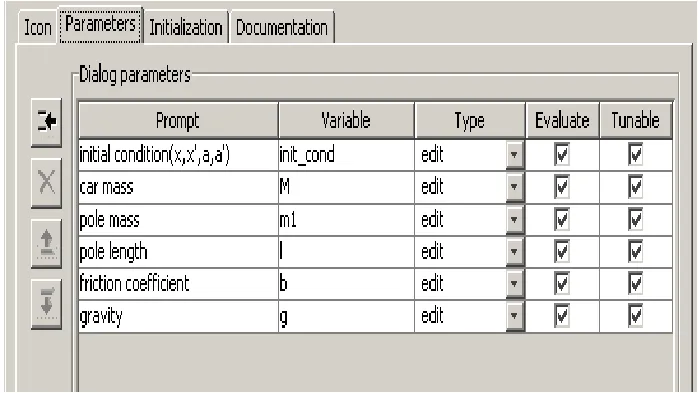
图6 子系统参数标签

图7 封装后的参数设计
3 结束语
在倒立摆仿真控制时,有时需要了解不同的初始状态下控制系统的响应,或者要了解系统在其他参数情况下的控制系统的响应,这时我们只要重新双击封装后的子系统模型,再重新输入新的参数值即可,从而使模型更具灵活性,给仿真带来很大方便。
[1] 固高科技(深圳)有限公司编著.倒立摆与自动控制原理实验[M].2005,24-27.
[2] 王正林,王胜开,陈国顺.MATLAB/Simulink与控制系统仿真[M].北京:电子工业出版社,2005.7:44-77.
Building the Simulation Model of an Inverted Pendulum
Zhai Longyu
( Jiangsu Finance and Economics College , Huai’an Jiangsu , China 223003)
This paper aims at an inverted pendulum system. It argues, after building a mathematical model on the basis of Newtonian mechanics, we can use Simulink and its MASK function to establish a simulation model of an inverted pendulum system,which can make the model more flexible and bring more convenience to the simulation.
inverted pendulum; mathematical model; simulation model
N945.12
B
1008-1151(2011)08-0268-03
2011-04-17
翟龙余(1966-),男,江苏姜堰人,江苏财经职业技术学院基础教学部副教授,硕士,从事高等数学与matlab应用教学。

