Excel在视准线小角法位移量计算中的应用

张付明，周 霁，何铁汉

（长江三峡勘测研究院有限公司，湖北 武汉430074）

1 引言

茅坪溪防护大坝是直线型的土石坝，主坝长为1 070m，坝顶高程为185m，防渗结构为沥青混土心墙，在大坝的迎水侧及背水侧分别布设了数条视准线，以监测大坝的横向水平位移。背水侧110m马道全长为574．2m。根据《混土大坝安全监测规范》和视准线的布设情况，按分段小角法进行施测。

Excel是一种“表格”式数据综合管理与分析系统，可以高效地完成多种多样的表和图的设计，进行复杂的数据计算和分析，良好的界面，强大的功能，便捷的操作已广泛应用于各行各业的办公系统的数据处理工作中，同样测量领域也能够发挥它的功效。基于上述优点，笔者将Excel用于计算长江三峡水利枢纽茅坪溪防护大坝视准线的水平位移，下面以茅坪溪防护大坝背水侧110m马道的视准线横向水平位移的计算为例，予以简述。

2 110m马道视准线的布设情况及观测方法

110m马道视准线长度为574m，在左右岸布设了两个端点及10个监测点，以视准线中间监测点AL05MP032为中间工作基点，将视准线分成左右两段观测。在AL05MP032上架设经纬仪，首先后视右端点，前视左端点，观测测站点至左、右两端点的大角（接近平角），然后分别以左、右端点为后视方向观测其它各监测点的小角。

3 110m马道视准线横向位移值的计算

3．1 两端点坐标旋转计算

在计算视准线横向水平位移值之前，首先要将两端点的大坝坐标系转换为茅坪坐标系，由茅坪坐标系计算各监测点的横向水平位移。茅坪坐标系的原点在大坝坐标系里是甲点，坐标为X0＝18 175．271，Y0＝50 630．278，茅坪坐标系的零方向在大坝坐标系的坐标方位角为A0＝276．142 1。

3．1．1 在“坐标旋转”工作表中设计“已知数据”表格

输入标题“已知数据”，在“已知数据”表中的B3、D3、F3中输入原点坐标值（X0、Y0）及起始方位角（A0）。为适应计算机计算，首先将A0角度60进制转换为10进制，公式为：

A＝Int（A0）＋Int（（A0－（Int（A0））×100））／60＋（（A0－Int（A0））×100－14）×100／3 600。

再将10进制角度转换为弧度。因此工作表中M5是将A0角度转换为十进制角度，转换后A0＝276．239 2，计算位移量时还要将十进制转换为弧度（图1）。

3．1．2 计算“原点”至“端点”的边长和坐标方位角

在“坐标旋转”工作表中设计“大坝坐标系”表格，输入标题“大坝坐标系”，将两端点的大坝坐标值（X、Y）分别输入B、D两列中，计算原点至各端点的距离和方位角，公式为：

Ai＝ATAN（（Y－Y0）／（X－X0））×180／PI（）＋360－A。

在Excel中建立2个工作表，分别命名为“坐标旋转”和“横向水平位移”。

图1 A0角度60进制转换为10进制计算

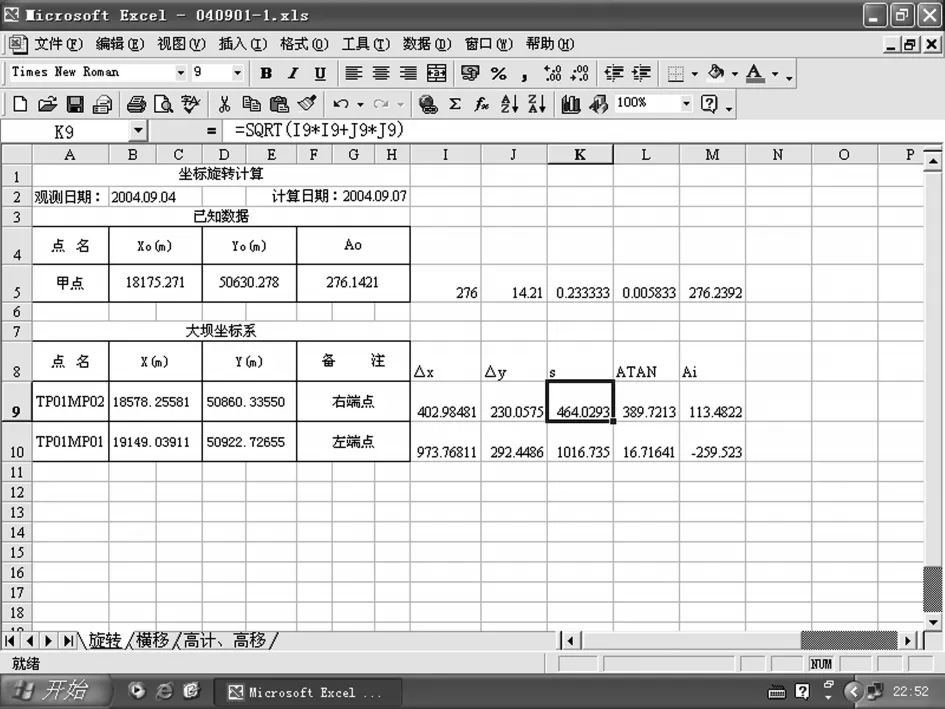
图2 原点至各端点的距离计算

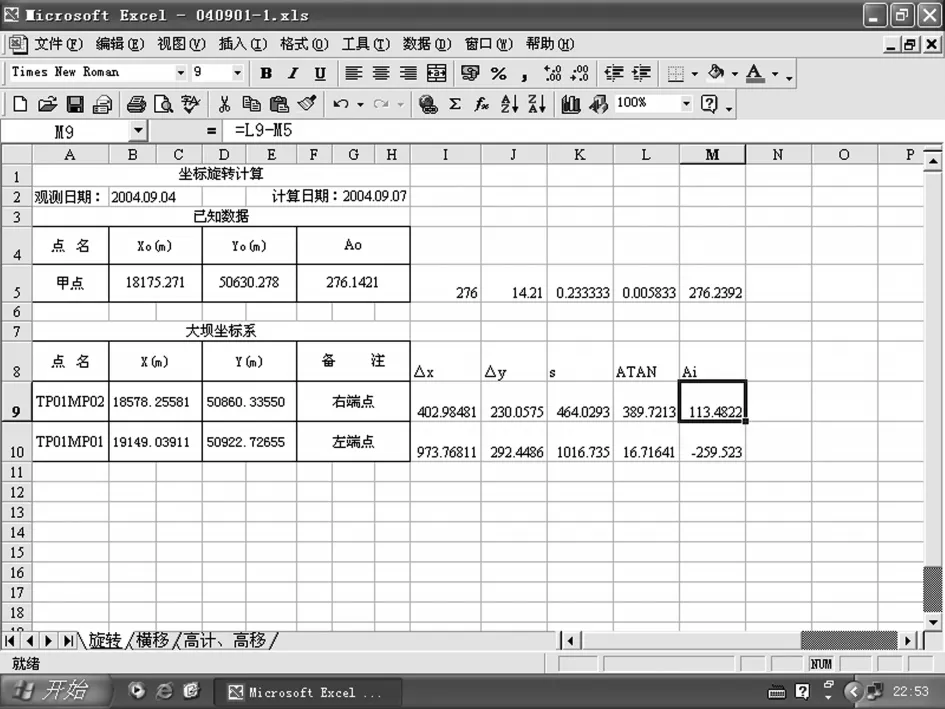
图3 原点至各端点的方位角计算

3．1．3 “大坝坐标系”转换为“茅坪坐标系”

在“坐标旋转”工作表中设计“茅坪坐标系”表格，输入标题“茅坪坐标系”，将两端点的大坝坐标利用坐标变换公式：

X＝S×COSAi，

Y＝S×SINAi。

计算得到两端点的茅坪坐标。输入标题“茅坪坐标系”，图中B列＝COS（M9×PI（）／180）×K9×1 000，D 列＝SIN（M9／180×PI（））×K9×1 000，B列、D列就为端点的茅坪坐标；如果有多个端点，拖拽下面各行列，就可得出其它端点的B列、D列值，见图4。

图4 “大坝坐标系”转换为“茅坪坐标系”计算

3．2 视准线横向位移值计算

3．2．1 视准线横向位移值计算的数学模型

数学模型见图5。

δ0＝（180°－r）×d1×d2／ρ×（d1＋d2），

Mi＝Ki×δ0±di×tgαi，

M＝Mi－Oi＋Ni（M左－M右）＋M右。

δ0为中间设站点的偏移值；r为左、右端点间的大角；d1为中间设站点至左端点的距离；d2为中间设站点至右端点的距离；Mi为监测点相对于设站点的偏移值；di为中间设站点至监测点的距离；αi为所测的小角；M为各监测点相对于两端点的偏移值；Oi为各监测点的首次偏移值；M左为左端点的偏移值；Ki＝K0×（d2＋di）／d2；M右为右端点的偏移值；Ni为系数；Ni＝（d1－di）／d1；ρ＝206 265″。

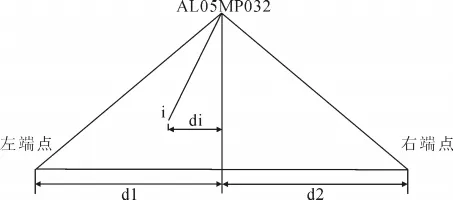
图5 视准线横向位移值计算的数学模型

3．2．2 视准线横向位移值计算

（1）计算两端点的累积位移量和月变化量。打开Excel中的“横向水平位移”工作表，设计“横向水平位移计算”表格，输入标题“110m马道视准线横向水平位移计算”。

端点的累积位移量＝X首－X本，

月变化量＝X上－X本。

在B6中输入端点首次值坐标X首，在C6中输入端点上月值坐标X上，在E6中输入端点本次值坐标X本，G6为端点的月变化量，G6＝C6－E6，H6为端点的累积位移量，H6＝C6－E6。如果有多个端点，可将其它端点的坐标值输入到相应的各行列中，将G、H列拖拽下面各行列，就可得出其它端点的月变化量和累积位移量。累积位移量和月变化量的计算见图6。

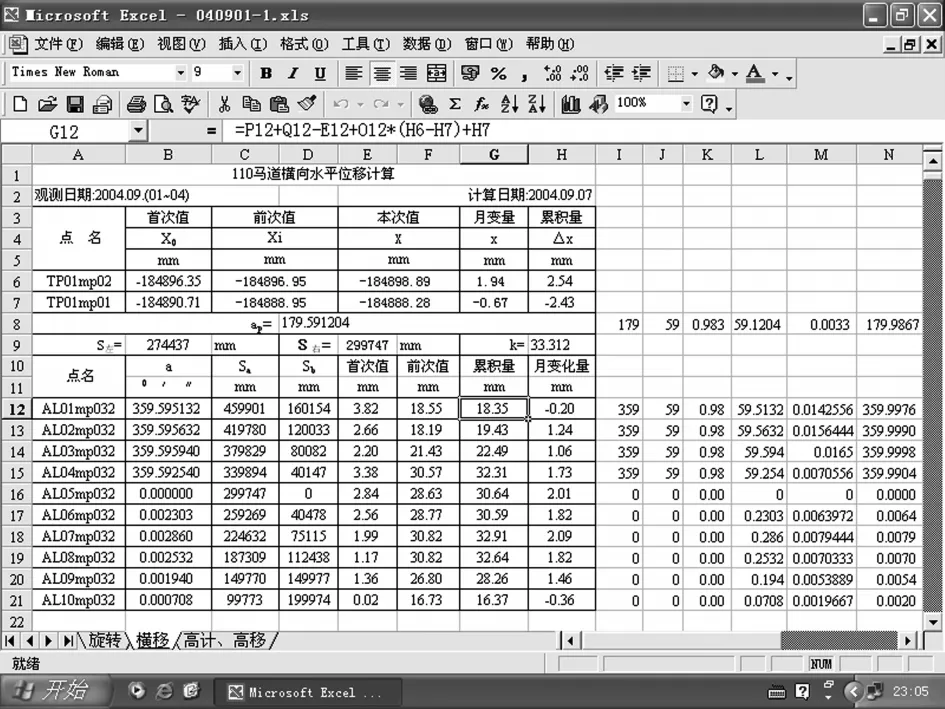
图6 累积位移量和月变化量计算表

（2）计算各监测点的横向位移。各监测点的横向位移计算公式前面已述，横向累积位移量＝M首－M本，横向月变化量＝M上－M本，表中A8为两端点的大角（AP），O8为对AP进行角度转换为弧度；H9为中间基点（AL05MP032）的横向水平位移量，A9中为左端点至中间基点的距离，C9为右端点至中间基点的距离，B列为所测各监测点的小角，C列输入所测各监测点至右端点的距离Sa，在D列为所测各监测点至中间基点的距离Sb，在E列为所测各监测点的横向位移首次值，F列为所测各监测点的横向位移上月值，

G列＝P12＋Q12－E12＋O12×（H6－H7）＋H7，（累积位移量的计算），

H列＝G12－F12（月变化量的计算）。

4 结语

通过对Excel的应用，可以很简便地进行表格的设计和函数公式编辑计算，可以重复进行计算和修改编辑，在测量中的运用最大特点是直观、简单、可以批量计算。

［1］王明华．中文Excel97培训教程［M］．北京：清华大学出版社，1998．

［2］李青岳，陈永奇．工程测量学［M］．北京：测绘出版社，1995．

［3］李 标．流溪河大坝采用全站仪进行水平位移监测的可行性研究［J］．科技创新导报，2009（35）：3～4．

［4］孙国峰．浅谈深基坑水平位移监测［J］．科技创新导报，2008（2）：49～50．