涤塔夫面料价格指数时间序列建模及实证分析

冯 岑，唐 琳，聂 博，刘炳娣，白 伦

(1.苏州大学 纺织与服装工程学院，江苏 苏州 215006；2.现代丝绸国家工程实验室，江苏 苏州 215123；3.中国丝绸工业总公司，北京 100034)

涤塔夫面料价格指数时间序列建模及实证分析

冯 岑1，2，唐 琳3，聂 博1，刘炳娣1，白 伦1，2

(1.苏州大学 纺织与服装工程学院，江苏 苏州 215006；2.现代丝绸国家工程实验室，江苏 苏州 215123；3.中国丝绸工业总公司，北京 100034)

就构建的涤塔夫面料价格指数及其市场运营数据曲线，采用经典的自回归移动平均模型ARMA和自回归异方差模型ARCH对涤塔夫产品系列各级指数进行时间序列建模和实证分析。经验证表明，已建立的时间序列模型对涤塔夫面料价格指数运行变化走势有很好的拟合效果，所建模型在置信理论区间内的预测值精度理想，可以进行对应的产品市场价格走势分析和预测。

数据采集；时间序列；预测模型；价格指数；涤塔夫面料

中国纺织品市场的统计数据多用于事后评估为主，因此对正在运行的市场分析预测存在时间滞后和定性为主的特点，如何充分运用已有的大量统计数据来即时判断市场发展趋势，值得研究和探索。本研究以实际区域市场运营为基础，就构建的涤塔夫面料价格指数曲线，通过单位根检验(Augmented Dickey-Fuller Test，ADF)序列测定时序的平稳性，经过平稳性转化、异方差效应检验、模型定阶等识别步骤，建立各自相应的时间序列模型[1-2]。对涤塔夫产品的单个品种和产品类价格指数走势的波动进行拟合和预测，实现对应的产品市场价格走势分析。

1 涤塔夫面料价格指数的数据采集

目前，区域市场已运营的化纤面料价格指数体系中，包括涤塔夫价格指数、轻盈纺价格指数、涤纶春亚纺价格指数等系列组成。其中涤塔夫价格指数又包含170T涤塔夫、190T涤塔夫、230T消光涤塔夫、260T消光涤塔夫等15个单品种价格指数。

以230T消光涤塔夫价格指数曲线获取相关数据。数据来源于中国绸都网(http://www.silkcapital.com/)，除国家法定节日外，230T消光涤塔夫价格指数每日在官网上公布，从中采集2009年8月1日到2009年12月31日230T消光涤塔夫价格指数，共100个数据。如图1所示，对应的100个数据组成了230T涤塔夫价格指数时间序列。同理，在相同时间区域内以各自曲线走势，获取其余14个单品种涤塔夫面料价格指数数据。

2 230T消光涤塔夫价格指数时间序列建模

运用Eviews软件[3]，对230T消光涤塔夫价格指数时间序列进行平稳性转换，作出自相关和偏关图，通过拉格朗日乘数检验(Lagrange Multiplier Test，LM)，判断此序列是否存在自回归异方差效应。根据相应价格指数波动特征建立自回归移动平均(Auto-Regressive and Moving Average Model，ARMA)模型或自回归条件异方差(Auto-Regressive Conditional Heteroskedasticity Model，ARCH)模型。

2.1 230T消光涤塔夫价格指数时间序列平稳性

时间序列的平稳性是时间序列建模的重要前提，选用ADF来判断时间序列的平稳性[4]。230T时间序列的平稳性转换结果如图2所示，对230T时间序列y进行二阶差分得到D2y时间序列，其检验值小于临界点的显著值，故D2y是平稳时间序列。

图1 230T消光涤塔夫价格指数时间序列变化曲线Fig.1 Time series curve of 230T delustering polyester tav price index fl uctuation

图2 D2y时间序列ADF检验图Fig.2 ADF testing of D2y time series

2.2 建立230T消光涤塔夫价格指数时间序列模型

2.2.1 230T消光涤塔夫时间序列相关性

图3表明，D2y时间序列的自相关、偏相关系数均显著，并呈现拖尾性。D2y时间序列模型可以尝试AR(1)、AR(3)、AR(4)、MA(2)、MA(3)、ARMA(3,2)、ARMA(3,3)、ARMA(4,2)、ARMA(4,3)等模型。通过各个模型参数比较和信息标准法则(Akaike Information Criterion，AIC)，获取最适合230T消光涤塔夫价格指数AR(4)模型为：

D2yt＝－0.884(D2yt-1－0.000 3)－0.771(D2yt-2－0.000 3)－0.582(D2yt-3－0.000 3)－0.357(D2yt-4－0.000 3)＋εtt＝1，2，3，…，T

图3 D2y时间序列自相关、偏相关图Fig.3 Autocorrelation and partial correlation fi gure of D2y time series

2.2.2 建立230T消光涤塔夫时间序列ARCH模型

图4为建立ARCH(4，1)模型过程，各项系数的概率均小于0.05，获得D2y时间序列ARCH(4，1)模型。

图4 D2y时间序列ARCH模型Fig.4 ARCH model of D2y time series

D2yt＝－0.000 553－0.878 370(D2yt-1－0.000 553)－0.731 068(D2yt-2－0.000 553)－0.627 641(D2yt-3－0.000 553)－0.330 686(D2yt-4－0.000 553)＋εtt＝1，2，…，T εt＝0.040 557－0.126 399ε2t-1t＝1，2，…，T

2.3 230T涤塔夫价格指数拟合和预测

图5为D2y时间序列ARCH的拟合图，将实际值与模型的预测值进行比较验证。从原先指数已经获取的100个数据基础上，继续按曲线走势摘取编号为101～110的10个数据作为实际值，表1显示了实际值与预测值的比较结果。统计表明：经过时间序列建模过程的数据处理和模型判断与选择，没有失去原始数据提供的信息，数据的绝对误差和相对误差呈波动增长趋势，预测精度达到较为理想的效果，特别适合市场波动的短期预测与指标统计。

图5 D2y时间序列ARCH拟合示意Fig.5 ARCH fi tting of D2y time series

表1 230T涤塔夫价格指数实际值与预测值的比较Tab.1 Comparisons between actual and predicted value of 230T delustering polyester tav

表2 各品种涤塔夫价格指数的ARCH模型系数Tab.2 ARCH coeff i cients for every kinds of polyester tav price index

3 各单品种涤塔夫价格指数时间序列模型

以230T消光涤塔夫的建模步骤和方式，分别对各品种涤塔夫产品的价格指数进行时间序列平稳性转换，取自相关和偏相关图，检查其自回归异方差效应是否存在。根据各自指数的数据波动特征及验证，分别建立ARCH和ARMA模型[5]。

ARCH模型：

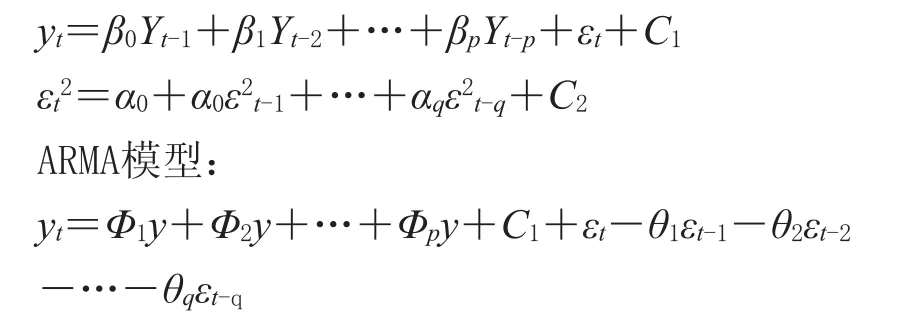
在15个单品种涤塔夫价格指数时间序列模型中，有10个具有ARCH效应，模型系数见表2。表明这些价格指数波动具有尖峰后尾的特征，即是均值附近与尾区的分布的概率值比正态分布大，而其余区域的概率比正态分布小；也表现出这些价格指数波动的群集性，即方差在一个集中时段比较小，在另一个集中时间比较大，波动的不确定性在不同的预测期间会有改变，且变化激烈。

5个单品种涤塔夫价格指数时间序列符合自回归移动平均ARMA模型，模型系数见表3。适合ARMA模型的单品种涤塔夫价格指数时间序列系统在n时刻的响应Yn和以前的响应Yn－1，Yn－2，…，Yn－p的相关性减弱，而与本身系统的扰动εn－1，εn－2，…的相关性增强。

4 涤塔夫面料价格指数时间序列模型

涤塔夫产品类价格指数是化纤面料指数中的二级指数之一，同前述方法获取相应的走势曲线和对应的时间序列数据，建立如图6所示的适合涤塔夫产品类价格指数走势的时间序列模型。

4.1 涤塔夫面料价格指数模型建立

由于涤塔夫产品类价格指数是由多个单品种涤塔夫价格指数综合加权平均得到，期间单品种价格指数波动尖峰被削去，变化曲线趋于平缓，所以涤塔夫价格指数时间序列也相对平稳。使用最小二乘法估计涤塔夫价格指数自回归模型系数，通过LM和模型识别，适合涤塔夫价格指数时间序列呈AR(5)模型，同时经验证不具备ARCH模型的效应。

D2yt＝－0.000 8－0.919 3(D2yt-1－0.000 8)－0.988 3(D2yt-2－0.000 8)－0.765 6(D2yt-3－0.000 8)－0.702 7(D2yt-4－0.000 8)－0.374 3(D2yt-5－0.000 8)＋vt

表3 各品种涤塔夫价格指数的ARMA模型系数Tab.3 ARMA coeff i cients for every kinds of polyester tav price index

表4 涤塔夫价格指数预测值与真实值比较Tab.4 Comparisons between actual and predicted value of polyester tav price index

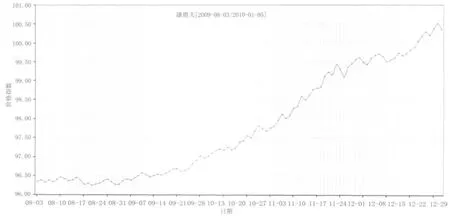
图6 涤塔夫系列面料价格指数时间序列变化曲线Fig.6 Time series curve of polyester tav fabric price index fl uctuation

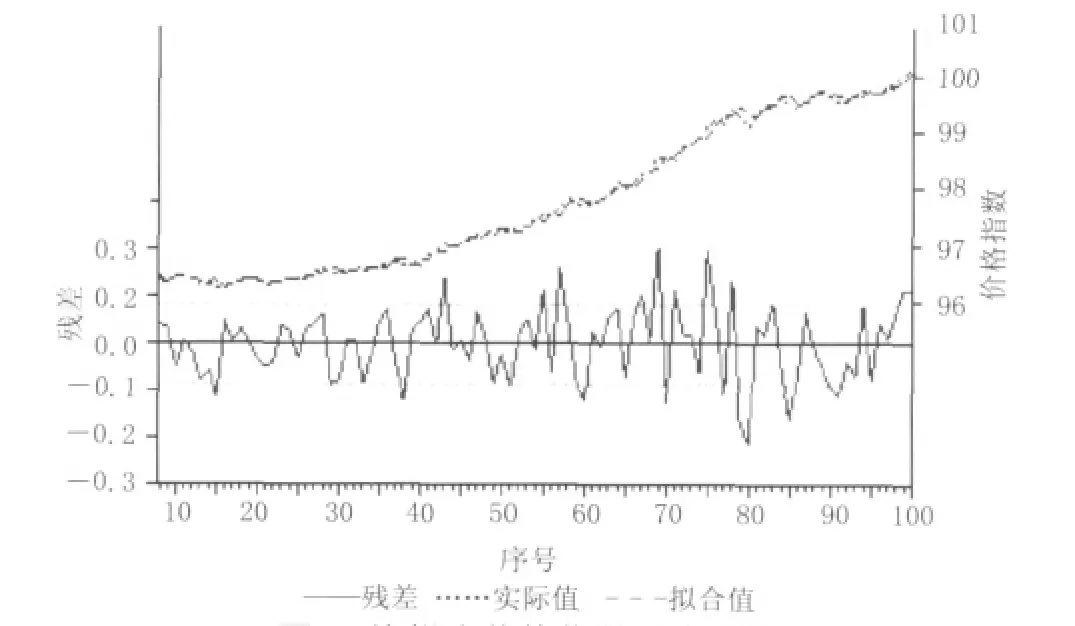
图7 涤塔夫价格指数拟合示意Fig.7 Fitting of polyester tav fabric price index

4.2 涤塔夫面料价格指数模型拟合和预测

图7为涤塔夫面料类别价格指数的拟合图。运用该模型预测获取5个数据呈拟直线增长，符合AR模型本身为线性模型的理论依据。由于涤塔夫价格指数数值变化区间小，其时间序列相对较平稳，将实际运营的统计数据与预测数值比较可看出，其预测精度很高，如表4所示。

从以上建模和分析可以看出，产品类别价格指数预测值的相对误差和绝对误差均小于单个品种的相关预测值，表明运用时间序列的建模方法更加适合于采集的每个数据包含大量信息的统计分析和预测。所有价格指数预测误差的趋势均随时间点延长逐步放大，因此该建模方法更加适宜于短期预测和分析。

5 结 语

通过采集单品种面料和产品类价格指数的相关数据，结合建模理论和Eviews软件，依时间序列模型识别步骤，可以建立经典的自回归移动平均模型ARMA和自回归条件异方差模型ARCH，并就运行变化走势的波动进行拟合和预测。

分析表明，单品种面料价格指数的相对误差和绝对误差均大于产品类别的相关值，表明运用时间序列建模预测方法更加适合于波动尖峰被削去、趋势变化平缓的曲线。由实际的检验证明：预测误差随时间的延长逐步放大，同时预测是在相对稳定的微观条件下进行，未考虑市场其他要素的变化，因此该建模方法更加适宜于短期预测和分析。

[1]BROCKWELL,PETER J.Introduction to time series and forecasting[M].北京：人民邮电出版社，2009.

[2]潘晓君.中国棉花产量的时间序列预测模型[J].统计与决策，2007(17)：59.

[3]张晓峒.Eviews使用指南与案例[M].北京：机械工业出版社，2007.

[4]高铁梅.计量经济分析方法与建模[M].北京：清华大学出版社，2009.

[5]张晓峒.计量计量经济学基础[M].天津：南开大学出版社，2007.

Time series modeling and empirical analysis on the price index of polyester tav fabric

FENG Cen1,2, TANG Lin3, NIE Bo1, LIU Bing-di1, BAI Lun1,2
(1.College of Textile and Clothing Engineering, Soochow University, Suzhou 215006, China; 2.National Engineering Laboratory for Modern Silk,Soochow University, Suzhou 215123, China; 3.China Silk Industrial & Trading Corporation, Beijing 100034, China)

This paper makes empirical analysis on Price Index of every level of Polyester tav fabric with classical ARMA models as well as ARCH models, which based on Polyester tav fabric Price Index and operating curve. The model validation suggests that there is good effect in running change of Polyester tav fabric Price Index for the time series models that has been established, the precision of the established model within the theoretic conf i dence interval is ideal.As a result, it can be used to analyze and predict for the corresponding market price trend.

Data collection; Time series; Predictive model; Price index; Polyester tav fabric

TS941.4；F224.0

A

1001-7003(2011)02-0028-04

2010-10-18；

2010-11-11

江苏省高校研究生科技创新计划(CX10B-037Z)；江苏省丝绸工程重点实验室项目(KJS0916)

冯岑(1964― )，女，副教授，博士研究生，研究方向为数字化纺织技术与产品开发。通讯作者：白伦，教授，bailun@suda.edu.cn。