工业集聚与劳动生产率的空间计量经济分析
——来自我国东北34个城市的经验证据
连 飞
(天津财经大学 统计系,天津300222)
工业集聚与劳动生产率的空间计量经济分析
——来自我国东北34个城市的经验证据
连 飞
(天津财经大学 统计系,天津300222)
本文以产业集聚与劳动生产率之间的关系为理论基础,将城市工业劳动生产率的空间相关性和异质性纳入分析框架,分别建立全域和局域空间计量模型,对我国东北地区城市工业集聚与劳动生产率之间的关系进行研究。研究发现,东北34个城市的工业劳动生产率总体上存在明显的空间溢出效应;工业物质资本和人力资本对工业劳动生产率具有积极的促进作用;工业劳动生产率对工业集聚规模的依赖性较大;工业的集聚发展产生了一定程度的拥挤效应。
工业集聚;劳动生产率;空间溢出效应;集聚规模;产业集聚
一、引言
产业集聚是当今国际上最为重要的经济现象之一,它指的是在一个经济区域内生产某种产品的若干个同类企业,以及为这些企业配套的上下游企业和相关服务业高密度地聚集在一起的产业现象和经济过程。越来越多的国家把产业集聚作为产业发展的战略方式,产业集聚已成为全球经济发展的潮流之一。通过实施产业集聚战略,促进产业结构优化升级,同样是我国“十二五”时期东北老工业基地全面振兴的关键。2009年我国政府发布的《国务院关于进一步实施东北地区等老工业基地振兴战略的若干意见》中明确提出,扶持东北地区重点产业集聚区加快发展,推动辽宁沿海经济带、沈阳经济区、哈大齐工业走廊、长吉图经济区加快发展,建设国内一流的现代产业基地。同年,相继批准实施的两项富有针对性的区域性政策文件《辽宁沿海经济带发展规划》和《中国图们江区域合作开发规划纲要》中也强调,加快老工业基地调整改造,必须遵循产业集聚规律。因此,在东北地区进入全面振兴的新时期,研究老工业基地的产业集聚问题具有重要的现实意义。
国内外学者对产业集聚与劳动生产率之间的关系已经进行了一些实证研究。Ciccone和Hall分析了美国各州的劳动生产率与就业密度之间的关系,发现经济集聚产生的规模收益递增对解释美国各州间劳动生产率的差异至关重要,一个地区的就业密度提高,劳动生产率也将随之提高[1]。Bode在对Ciccone和Hall的研究作了一定扩展后,利用德国的数据进行分析,发现用人口密度衡量的经济集聚水平对劳动生产率的影响并不显著[2]。范剑勇利用我国2004年各地级及副省级城市的数据分析得出,非农产业劳动生产率对非农就业密度的弹性高于欧美国家,且这一集聚效应在各省之间存在有差异和无差异两种情况,在非农产业分布极不平衡的情况下,扩大了劳动生产率在各省之间的差异[3]。柯善咨和姚德龙利用2005年的数据对我国地级及以上城市的工业集聚和劳动生产率进行了截面分析,结果表明我国城市就业的空间密度过高,其拥挤效应导致生产率降低[4]。
上述文献大多是直接借鉴Ciccone和Hall的理论模型,结合现实问题进行的经验分析,得出了有一定参考价值的结论,也证实了该模型对研究产业集聚与劳动生产率关系问题是有效的。然而,该模型对集聚经济的测度只有产出密度,没有集聚规模。事实上,工业集聚经济效应的大小在某种程度上也有赖于工业集聚规模,因为一个城市工业集聚规模越大,工业经济联系越紧密,在集聚经济效应作用下,工业劳动生产率可能越高。柯善咨和姚德龙用工业产值比构造工业集聚指数,并把它作为工业集聚规模的代理变量[4],但一个城市较高的工业产值比可能是由于单个或少数几个大企业的存在所导致的,即产值指标不能准确反映工业集聚规模。由于一个城市工业企业数的上升,表明在该城市发生了工业的集聚,所以本文认为可以用工业企业相对数指标反映工业集聚规模,以便更科学、系统地研究工业集聚规模经济效应对工业劳动生产率的影响。
由于知识、技术、劳动力以及中间生产部门会在城市之间流动或为邻近城市提供服务,因此经济外部性不仅存在于城市内部,而且会跨越城市边界,于是导致邻近城市之间的工业劳动生产率在一定程度上会互相影响,这意味着工业劳动生产率会溢出至邻近的城市。所以,在研究工业集聚与劳动生产率之间的关系时,如果仍像传统研究思路那样忽视空间维度的相关性和异质性,在模型设定上将会存在严重不足。为了得到关于工业集聚与劳动生产率之间关系的更准确的结论,我们应对其进行空间计量经济分析。本文拟借鉴Ciccone和Hall的产业集聚与劳动生产率的关系理论[1],并将城市工业劳动生产率的空间相关性和异质性纳入分析框架,通过分别建立全域和局域空间计量模型,对我国东北地区城市工业集聚与劳动生产率之间的关系进行研究。
二、理论框架
Ciccone和Hall认为集聚经济效应源于经济活动的分布密度,且集聚经济效应将带来经济效率的改进[1]。他们将集聚水平界定为单位土地面积的某产业劳动力数量,并用劳动生产率指标来反映经济效率的改进。考虑到影响劳动生产率的因素还包括物质资本、人力资本、技术进步和自然条件等,于是他们提出了如下研究产业集聚与劳动生产率之间关系的基础理论模型,本文将其应用到工业部门:

其中:i表示第i个城市;Y为工业总产出;S为土地面积;A为工业全要素生产率;K为工业物质资本存量;L为工业劳动力数量;h为劳动力质量,即人力资本;α为单位土地面积工业物质资本和劳动力的回报;1-β和β分别为工业物质资本和劳动力的贡献率;(λ-1)/λ为单位土地面积工业产出对外部性的弹性系数,表示单位土地面积工业产出对整体工业产出密度的反应。
上述模型能够比较全面地反映各生产要素及产出密度对劳动生产率的影响。然而,本文除了用工业经济活动的分布密度对工业集聚程度进行测度外,还加入工业企业相对数指标反映工业集聚规模,于是,式(1)扩展为:

其中:ri为工业企业相对数,等于城市i的工业企业数在所有城市工业企业数中所占的比重;γ为未知参数。
将式(2)两边乘以土地面积,并除以工业劳动力数量,再对其他因子做适当变换,即可得到工业劳动生产率为:

其中:当αλ=1时,不存在规模报酬递增,即工业就业密度对劳动生产率的净效应为0;当αλ>1时,存在规模报酬递增,即工业就业密度对劳动生产率的净效应为正,工业物质资本或人力资本由于趋利性而从外部持续流入该城市,城市工业集聚效应将进一步放大;当αλ<1时,存在规模报酬递减,即工业就业密度对劳动生产率的净效应为负,单位土地面积集聚的工业物质资本和劳动力过多,拥挤成本超过集聚效应,产生了负外部效应。

其中:y为工业劳动生产率;k为工业劳均物质资本;l为单位土地面积工业劳动力数量,即工业就业密度;β0=λln Ai,表示技术进步、自然条件、社会环境以及市场化程度等不可观测因素;β1=(1-β)αλ,表示工业劳动生产率对工业劳均物质资本的产出弹性;β2=βαλ,表示工业劳动生产率对人力资本的产出弹性;β3=αλ-1,表示工业集聚的正外部性与拥挤成本的负外部性相抵后的净效应;β4=γ(λ-1),表示工业劳动生产率对工业企业相对数的产出弹性。式(4)即为本文的实证模型。
三、实证分析
(一)数据及变量说明
本文以我国东北三省地级及以上城市的市辖区为研究对象,选取2008年东北三省34个城市的横截面数据,数据来源于2009年《中国城市统计年鉴》。其中,各工业指标的口径均为规模以上工业企业。下面对实证分析中各变量作一简要介绍。
1.工业劳动生产率y。工业劳动生产率用工业总产值除以工业从业人员年平均人数得到,单位为万元/人·年。采用工业总产值而非工业增加值计算工业劳动生产率的理由在于,工业总产值能更好地反映工业生产规模,同时考虑数据的可得性及相关指标口径的一致性,因而使用了总产值指标。
2.工业劳均物质资本k。本文用工业企业流动资产年平均余额与固定资产净值年平均余额之和表示工业物质资本存量,然后将其除以工业从业人员年平均人数,即得到工业劳均物质资本,单位为万元/人·年。
3.人力资本h。通常用劳动力受教育年限或成人识字率来测度人力资本,但本文无法得到所需的各城市相应数据;每万人大学在校学生数也经常作为人力资本较好的代理变量,但大学在校学生数在地级市的人口中所占的比重较小。因此本文借鉴张艳和刘亮、吴玉鸣等人的人力资本指标设定方法[5][6],采用城市每万人中的中小学在校学生人数作为人力资本的衡量指标,该指标能够较好地反映地级市的教育发展状况以及人力资本水平,它等于中小学在校学生人数之和除以年末总人口,单位为人/万人。
4.工业就业密度l。工业就业密度作为工业集聚程度的代理变量,反映工业经济活动在空间上的分布差异,它等于工业从业人员年平均人数除以城市建成区面积,单位为人·年/平方公里。
5.工业企业相对数r。工业企业相对数作为反映城市工业集聚规模的变量,它等于一个城市工业企业数占所有城市工业企业数的比重,单位为%。
(二)全域和局域空间相关性分析
首先,借助全域Moran’s I分析东北地区城市工业劳动生产率y的空间相关性。2008年东北34个城市工业劳动生产率的Moran’s I为0.299 6,而且Moran’s I的正态统计量Z值大于正态分布函数在1%水平上的临界值1.96,这意味着东北地区相邻城市之间的工业劳动生产率在地理分布上具有明显的正空间相关关系,工业劳动生产率在空间上不是分散分布的,而是表现出具有较高工业劳动生产率的城市相对地趋于和其他具有较高工业劳动生产率的城市相靠近、具有较低工业劳动生产率的城市也相对地趋于和其他具有较低工业劳动生产率的城市相靠近这样一种空间联系结构。
其次,利用局域Moran’s I散点图进行局域空间相关性分析。该相关性分析显示了2008年东北34个城市工业劳动生产率的局域空间分布情况。其中,沈阳、大连、鞍山、抚顺、本溪、锦州、营口、辽阳、盘锦、铁岭、葫芦岛、长春、吉林、松原等14个城市位于第一象限(HH),表现为正的空间相关关系,是工业劳动生产率较高地区的集群,且效率在不断强化;哈尔滨、齐齐哈尔、鸡西、鹤岗、双鸭山、伊春、佳木斯、七台河、牡丹江、黑河、绥化等11个城市位于第三象限(LL),同样表现为正的空间相关关系,但为工业劳动生产率较低地区的集群,且效率在不断弱化;丹东、阜新、朝阳、四平、辽源、白山、白城等7个城市位于第二象限(LH),通化、大庆等2个城市位于第四象限(HL),这两个象限均表现为负的空间相关关系,但位于这两个象限的城市相对较少。
通过Moran’s I散点图识别出2008年东北地区有25个城市表现了相似的空间关联,9个城市表现了非相似的空间关联,说明东北地区城市工业劳动生产率的空间局域相关性和异质性同时存在。此外,沈阳、大连、长春等东北中心城市及其附近地区大多位于第一象限,显示出了工业劳动生产率的“核心—边缘”空间分布格局,即局部高值(东北中心城市及其附近)地区的工业劳动生产率较高,而局部低值(偏离东北中心城市)地区的工业劳动生产率较低。因此,为全面提高东北地区整体工业劳动生产率,应充分利用中心城市对其他城市产生的空间溢出效应,特别是对偏离中心城市的地区,应进一步加大铁路、高速公路等交通运输基础设施建设的投入力度,不断增强城市之间的工业经济联系,从而有效发挥中心城市的高端辐射作用,引领东北地区向新型工业化目标迈进。
空间相关性检验证明了东北34个城市的工业劳动生产率存在明显的空间相关性,为此,我们将分别对式(4)进行全域和局域空间计量分析。
(三)全域空间计量分析
首先,对式(4)建立经典回归模型,并采用普通最小二乘法(OLS)进行估计,结果如表1所示。此时,工业劳均物质资本k、工业就业密度l和工业企业相对数r的弹性系数都通过了5%水平的显著性检验,但常数项c和人力资本h的弹性系数不显著。对经典回归模型的误差进一步计算空间相关指数Moran’s I,检验其空间相关性,结果表明,Moran’s I(误差)在10%的水平上显著,这说明经典回归模型的误差仍存在空间相关性。所以,就该问题而言,假定截面单元之间相互独立而采用OLS估计是不可取的,正确的做法是考虑空间相关性并建立空间计量模型。
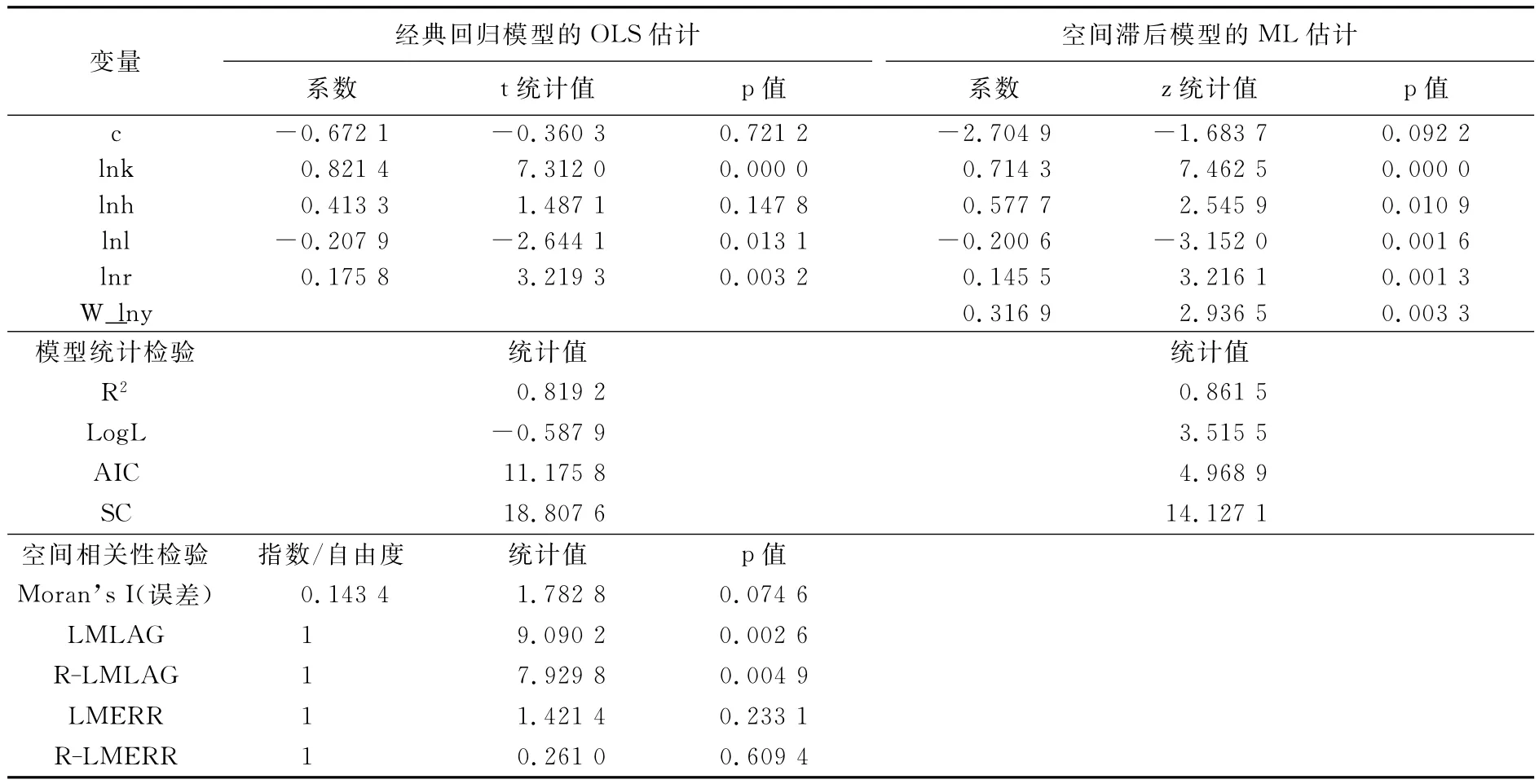
表1 经典回归模型和空间滞后模型的回归结果
为了进一步区分这种空间相关到底是内生的空间滞后还是空间误差自相关,我们进行了两个拉格朗日乘数的空间相关性检验[7](P104-112)。结果发现LMLAG在1%水平上比LMERR更为显著,且R-LMLAG在1%水平上较显著而R-LMERR不显著,因此,空间滞后模型(SLM)是更恰当的模型形式。
其次,对式(4)建立SLM,并采用极大似然(ML)估计,结果如表1所示。由表1可知,除常数项c外,其余各变量的弹性系数均通过了5%水平的显著性检验。而且,对比经典回归模型和SLM的检验结果,我们不难发现,SLM的拟合优度R2和对数似然值Log L均较大,而AIC和SC值则较小,因此,SLM相对更好一些。可见,SLM作为对忽视了地理空间效应的经典回归模型的修正,消除了模型误差的空间相关性,纠正了模型的设置偏误,结果更为准确可靠。下面,我们对SLM估计参数的经济含义作一简要分析。
工业劳动生产率对工业劳均物质资本k的弹性系数最大,达0.714 3,表明加大工业物质资本投入不仅能够带来先进的技术和管理,而且通过技术外溢和前后向关联可以提高整个城市的工业劳动生产率。振兴东北老工业基地战略实施以来,东北地区凭借优惠的引资政策、便利的交通条件和良好的工业基础吸引了大量的物质资本进入,不仅提高了工业企业自身的生产效率,而且通过各种渠道“外溢”给当地企业,推动了东北工业经济的快速发展。工业劳动生产率对工业劳均物质资本的弹性系数显著为正,正是这一实际情况的真实写照。
工业劳动生产率对人力资本h的弹性系数较大,为0.577 7,表明东北地区人力资本对城市工业劳动生产率具有积极的促进作用。事实上,通过培育人力资本优势,可以加快新知识、新技术的扩散,对东北地区城市工业发展具有重要意义。因此,这一分析结果同样是合理的。
工业劳动生产率对工业就业密度l的弹性系数为-0.200 6,这一结果正好说明随着工业经济活动的集聚,环境污染将不断加剧,要素成本也会上涨,东北地区工业的集聚已经导致一定程度的要素拥挤(特别是劳动力的拥挤)和边际报酬递减。究其原因,可能有三:一是虽然在东北地区的城市集中了大批工业企业,但专业化分工程度很低,并未形成真正意义上的工业集聚,从而严重影响了企业竞争力的提高和工业规模优势的发挥;二是东北地区国有经济占有很大比重,由于体制、管理等方面的原因,普遍存在适应市场能力低,从而生产效率低的问题;三是东北地区产业结构调整升级迟缓,导致许多老工业企业在走下坡路的同时,新的工业企业没有能够脱颖而出[8]。
工业劳动生产率对工业企业相对数r的弹性系数为0.145 5,意味着东北地区城市工业劳动生产率对工业集聚规模也有一定程度的依赖性,城市工业企业只有达到一定的数量和规模,集聚效应才能显现出来,即城市会从工业规模经济中获益。我国政府为实施东北振兴战略,积极加大对老工业基地的投入力度,东北地区涌现出一批新型工业企业,企业间联系更加紧密,极大地降低了企业生产成本,有效地提高了工业劳动生产率水平。我们的模型估计结果正好印证了这一事实。
邻近城市劳动生产率W_lny的空间自回归系数为0.316 9,表明东北地区城市工业劳动生产率在地理空间上确实存在较强的溢出效应,一个城市的工业劳动生产率不仅可以增强自身的竞争力,还会溢出到邻近城市,使邻近城市工业劳动生产率随之增强。
此外,常数项c为-2.704 9,且仅在10%的水平上显著,意味着东北地区的自然地理条件、对外开放以及市场化程度等其他一些未明确控制的因素,对工业劳动生产率的提高作用不明显。
(四)局域空间计量分析
空间地理加权回归模型(GWR)考虑了空间距离和局域的空间联系,能够将地理空间异质性纳入模型框架,使变量间的关系随着空间位置的变化而变化,通过对回归系数的局域分解获得差异化的估计结果。为此,我们利用加权最小二乘法(WLS)对式(4)进行局域估计。
经计算发现,分别以高斯距离权值、指数距离权值和三次方距离权值得到的3个GWR的参数估计结果基本一致,且它们的拟合优度R2均高于SLM,这说明假定回归系数随着空间位置的变化而变化更符合东北34个城市的实际,工业劳动生产率确实存在一定程度的空间关联及非均质性。同时,三次方距离权值的GWR整体拟合效果最好,R2达0.933 3,且模型中各变量的显著性水平也优于高斯距离权值和指数距离权值的GWR。因此,本文选择三次方距离权值的GWR进行分析。表2给出了东北34个城市三次方距离权值的GWR的参数估计结果。

表2 GWR参数估计结果
整体来看,局域和全域空间计量估计结果基本一致,但不同城市之间各系数的相对大小及显著程度有所不同,具体表现在:
工业劳动生产率对工业劳均物质资本k的弹性系数在各城市之间几乎均通过了5%水平的显著性检验,且估计值均较高,表明对东北地区多数城市来说,工业劳均物质资本是工业劳动生产率的重要决定因素。其中,白城、齐齐哈尔、大庆等3个城市的系数在5%的水平上不显著;抚顺、本溪、丹东、铁岭、长春、吉林、四平、辽源、通化、白山、松原、哈尔滨等12个城市的系数相对较小,其值在0.430 9~0.636 1之间;其余19个城市的系数相对较大,其值在0.730 6~1.102 9之间,说明物质资本作为工业生产的要素投入主体,承担着工业生产的主要角色,在提高工业劳动生产率中居于主导地位。
工业劳动生产率对人力资本h的弹性系数均为正,但其统计检验的显著程度在各城市之间差异相对较大。其中,锦州、阜新、朝阳、白城、哈尔滨、大庆等6个城市的系数相对较大,其值在0.859 5~1.775 7之间,说明其工业生产对掌握并积累了一定技能的劳动力以及受到良好教育的人力资本的依赖性较大;抚顺、本溪、丹东、辽源、通化、白山等6个城市的系数相对较小,其值在0.463 9~0.718 1之间;其余22个城市的系数在5%的水平上不显著,这一估计结果可能反映出这些城市的发展仍依赖于资本和廉价的劳动投入,人力资本对城市工业劳动生产率的贡献有限,以及大量毕业生异地就业等现实。
工业劳动生产率对工业就业密度l的弹性系数在各城市之间大部分通过了5%水平的显著性检验,且估计值均为负。其中,本溪、长春、吉林、通化、白山、松原、白城、齐齐哈尔、鹤岗、双鸭山、大庆等11个城市的系数在5%的水平上不显著;抚顺、四平、辽源、哈尔滨、鸡西、伊春、佳木斯、七台河、牡丹江、黑河、绥化等11个城市的系数相对较大,其值在-0.477 5~-0.152 1之间;其余12个城市的系数相对较小,其值在-0.893 0~-0.531 1之间,这意味着工业就业密度每增长1%,将使工业劳动生产率减少约0.531 1%~0.893 0%,说明其工业就业密度对工业劳动生产率的负面影响相对较大,即拥挤效应较大。
工业劳动生产率对工业企业相对数r的弹性系数在各城市之间大部分通过了5%水平的显著性检验,且估计值几乎均为正。其中,沈阳、鞍山、锦州、阜新、盘锦、朝阳、葫芦岛、通化、黑河、绥化等10个城市的系数相对较小,其值在0.113 91~0.155 8之间;抚顺、丹东、铁岭、四平、辽源、白山、松原、白城、哈尔滨、齐齐哈尔、大庆等11个城市的系数相对较大,其值在0.160 6~0.302 0之间,这意味着工业企业相对数每增加1%,将使工业劳动生产率增长约0.160 6%~0.302 0%,说明其工业企业相对数对工业劳动生产率具有较高的贡献;其余13个城市的系数在5%的水平上不显著。
四、结论及政策含义
本文的研究表明:东北34个城市的工业劳动生产率总体上存在明显的空间溢出效应,且空间局域相关性和异质性同时存在;工业劳均物质资本是东北地区城市工业劳动生产率的重要决定因素,且其促进作用在各城市均相对较高;人力资本对城市工业劳动生产率的提高同样发挥积极的作用,且其影响程度在各城市之间的差异相对较大;城市工业劳动生产率对工业集聚规模的依赖性较大,但工业的集聚发展也产生了一定程度的拥挤效应。
基于上述研究结论,我们认为:第一,为充分发挥沈阳、大连、长春等东北中心城市的辐射带动作用,形成一批具有核心竞争力的工业集群,必须加强东北地区铁路和公路运输等基础设施建设;第二,应进一步改善投资环境,增强企业吸收资本的能力,提高工业物质资本使用效率,实现从“粗放型”向“集约型”发展方式的转变;第三,应不断增强对高素质劳动力的吸引,加大对教育的投资力度,努力提高人力资本的规模和质量,充分发挥人力资本在工业经济发展中的作用;第四,应按照现代化大生产的要求,形成规范、稳定的有梯度层次的专业化分工协作,强化企业间的联系,建设一批有影响、有规模的特色工业园区,同时,要降低国有工业企业在整个工业中的比重,合理调整产业结构,发展县域工业经济,减少城市拥挤效应;第五,由于各城市自身条件的差异以及受到邻近城市影响的不同,各地政府有必要因地制宜制定差异化的城市工业发展战略,充分发挥自身优势,并利用邻近城市的有利因素发展本地工业经济,尽快实现东北老工业基地的全面振兴。
[1]Ciccone,A.,R.E.Hall.Productivity and Density of Economic Activity[J].American Economic Review,1996,86(1):54-70.
[2]Bode,E.Productivity Effects of Agglomeration Externalities[EB/OL].(2004-06-09)[2010-07-12]www.cournot2.u-strasbg.fr/sew/papers_sew/Bode_Eckhardt.pdf.
[3]范剑勇.产业集聚与地区间劳动生产率差异[J].经济研究,2006,(11):72-81.
[4]柯善咨,姚德龙.工业集聚与城市劳动生产率的因果关系和决定因素——中国城市的空间计量经济联立方程分析[J].数量经济技术经济研究,2008,(12):3-14.
[5]张艳,刘亮.经济集聚与经济增长——基于中国城市数据的实证分析[J].世界经济文汇,2007,(1):48-56.
[6]吴玉鸣.县域经济增长集聚与差异:空间计量经济实证分析[J].世界经济文汇,2007,(2):37-57.
[7]Anselin,L.Spatial Econometrics:Methods and Models[M].Dordrecht:Kluwer Academic Publishers,1988.
[8]吴月越.产业集聚:东北老工业基地的困境与出路——基于新经济地理学的分析视角[J].当代经济研究,2007,(1):38-41.
(责任编辑:胡浩志)
Spatial Econometric Analysis of Industrial Agglomeration and Labor Productivity:Based on Empirical Evidence of China's 34 Northeast Cities
LIAN Fei
(Dept.of Statistics,Tianjin University of Finance and Economics,Tianjin 300222,China)
This paper references the theory of relationship between industrial agglomeration and labor productivity and integrates the spatial correlation and heterogeneity of urban industrial labor productivity into the analysis framework.At the same time,the paper establishes a global and local spatial econometric model separately to conduct the research for relationship between industrial agglomeration and labor productivity of China's Northeast cities.The 34 Northeast city's industry labor productivities have obvious spatial spillover effect as a whole;industrial physical capital and human capital have positive promoting roles in the industrial labor productivity and industrial labor productivity largely dependent on industrial agglomeration scale.At last,agglomeration development of industry produced a certain degree of crowding effect.
Industrial Agglomeration;Labor Productivity;Spatial Spillover Effect;Agglomeration Scale;Industrial Agglomeration
F424.4
A
1003-5230(2011)01-0108-07
2010-11-18
连 飞(1983— ),男,吉林松原人,天津财经大学统计系博士生。

