银行客户信用评级系统合理性的检验——排序响应面板数据模型在银行风险管理中的运用

郑大川沈利生黄 震

（1．华侨大学 经济与金融学院，福建 泉州362021；2．华侨大学 数量经济与技术经济研究院，福建 泉州362021；3．中国社会科学院 数量经济与技术经济研究所，北京100732；4．奥特本大学 数学科学系，Ohio Westerville 43081）

银行客户信用评级系统合理性的检验
——排序响应面板数据模型在银行风险管理中的运用

郑大川1沈利生2，3黄 震4

（1．华侨大学 经济与金融学院，福建 泉州362021；2．华侨大学 数量经济与技术经济研究院，福建 泉州362021；3．中国社会科学院 数量经济与技术经济研究所，北京100732；4．奥特本大学 数学科学系，Ohio Westerville 43081）

贷款人信用评级是商业银行内部评级体系的基础，它对整个内部评级体系的效果有根本性的影响。银行的信用评级系统含有大量主观因素，会对评级效果产生影响。含随机效应（包含随机截距项和随机系数）的排序响应面板数据模型能够对现有银行信用评级系统的合理性进行检验和分析。实证结果表明，新模型可以发现现有系统的冗余指标，并为权重设置提供依据。据此为银行信用评级系统的修正提供了依据。

信用评级；面板数据模型；排序响应模型；随机效应

贷款人信用评级是商业银行内部评级体系的一个基础环节，它的准确程度对整个内部评级体系的效果有直接影响。信用评级的定义表述各有不同，但其核心理念是一致的：银行事先确定一系列影响信用风险的因素，通过定性和定量相结合的方法，对客户进行信用评级，这是判断客户偿债能力和违约概率的重要依据，也是商业银行提高管理水平、做到科学放贷、降低银行经营风险的重要内容。在《巴塞尔新资本协议》下，这更是银行进行资本监管和经济资本核算的基础。

中国各家商业银行已经积极投入内部评级体系的开发工作，开始研究和实施针对企业贷款申请客户的信用评级模型和系统。然而，新建立起来的各种信用评级系统有着诸多不成熟之处。坚持检验和改进现有信用评级体系，开发符合我国经济特点的信用评级模型，是我国银行业和银行监管部门的重要任务。本文将以国内某国有控股商业银行信用评级系统为例证，创新性地采用含随机效应的排序响应面板数据模型对其进行检验和分析，提出改进现有信用评级系统的思路和建议。

一、对银行信用评级系统进行计量模型检验的意义

目前银行的评级系统中包含了诸多主观判断成分，比如指标权重的设定和评议指标的分析判断，都是由专家打分得到，其结果难免有失客观性、公正性。为了科学合理地对客户进行信用评级，使评级结果更加准确，更有利于银行进行风险管理工作，合理分配银行资金，对现有信用评级系统进行科学计量检验就显得十分必要。然而对银行现有评级系统合理性进行研究的相关工作极为少见。现有文献更多的是直接探讨企业违约率预测模型的设定和选择，就评级系统检验工作而言，目前仅有王恒和沈利生所做的研究。王恒和沈利生使用排序多元离散选择模型对银行信用评级系统进行了研究和检验，并且根据实证结果提出了对现有信用评级系统的修正建议［1］。事实上，这一方面的研究工作是十分重要的，不仅具有理论意义，而且能更好、更直接地对实务工作进行指导。

首先，计量模型检验能够分析现有评级系统是否存在冗余指标。第一，如果某个指标对所有企业都可以得到大致相同的分数，该指标就不具备区分企业经营状态的能力，就是一种冗余指标。第二，由于信用评级所用指标由财务比率构成，分子或分母有可能是相同的财务指标，因此各个财务比率之间可能存在相关性，这样就容易导致冗余指标的产生。过多冗余指标增加了银行收集数据的难度，也增加了信用评级的成本，同时由于相关性的存在，也会造成最终评级结果统计推断上的偏误。第三，对不同企业，有些指标虽然取值不尽相同，但是它们对企业客户的最终评级结果影响甚微。如果某个指标的取值变化不能带来客户在信用等级上的显著变动，这也造成了指标的冗余现象。在统计计量模型中，指标的冗余直接表现为指标变量参数在统计上不显著或估计值过小。

其次，计量模型检验能够对现有评级体系的指标权重设置进行评估。现有评级体系的指标权重是专家打分得到的，掺杂了主观因素。这些权重是否合理，是否符合原先的设定原则，需要经过相应的检验才能知道。王恒和沈利生指出，根据排序模型的定量计算结果，既可以得到各指标的显著性水平，又可以得到各指标对评级的影响程度，这就有利于对信用评级系统做出客观评判，并为指标调整和分值调整指明方向［1］。

巴塞尔新协议的精神之一是允许银行根据自身情况开发、选择自己的风险预测模型，从而改变了旧协议“一刀切”的风险测量模式。对信用评级系统进行检验、调整，使其更加灵活合理地反映自身的市场特点和运营特点，这体现了巴塞尔新协议的核心精神，是内部评级领域的重要突破。

二、基于面板数据的离散选择模型

与基于截面数据的模型相比，面板数据分析带来的好处是明显的。首先，面板数据丰富了数据信息。它可以提供截面和时间序列两个维度的信息，增加了数据信息，使估计和预测的准确性得到很大提高。其次，面板数据分析在计算过程中允许缺失值的存在。因此，面板数据分析的估计结果更加有效，预测能力也更强。第三，面板数据分析降低了共线性的程度。由于信用评级数据存在观测对象的同质性，所以特别容易造成共线性的产生。正如Tucker指出的，各个财务指标之间可能因为相同的分子或分母，较容易产生共线性。将所有时期的数据简单纳入计算而不加以时序区分的做法是相当有害的［2］。面板数据模型能够增加各个变量的变异性，有效地减少共线性的危害。第四，最重要的是，面板数据能有效地把握观测对象的异质性。统计计量模型要求观测样本之间保证相互的独立性，然而在一般统计计量模型中，同一时期的观测个体不是绝对独立的，它们同时受到相同宏观经济环境因素的影响，面板数据模型综合地考虑了这些共同因素，并且在技术上将其进行区分。

面板数据模型使得经济计量分析更为全面、更为具体，因此得到了迅速的发展。然而目前大量的研究工作都是基于连续型因变量模型的。相比较而言，关于离散型因变量模型的面板数据研究少之又少。Ronghua和Hansheng指出：相对于大量关于连续响应的面板数据模型研究而言，二元响应面板数据模型研究要少得多；至于排序响应面板数据模型，相关的研究更是凤毛麟角［3］。而在实践中，后者又是有着现实意义的。

本文正是对这一领域的探索，将王恒和沈利生的检验思路扩展到面板数据分析领域，第一次引入含有随机效应的排序响应面板数据模型，以此对银行现有信用评级系统进行深入地分析和检验。Rabe－Hesketh和Skrondal等人将调适数值积分法和极大似然估计相结合，提出了解决离散响应面板数据模型的估计和预测方法［4］［5］。笔者将此方法用于模型参数估计和预测工作。

我们先介绍基于面板数据的排序响应模型基本框架。在这个基本框架中，暂不考虑模型中的随机效应。这实际上是一种“伪面板数据”模型。在现有使用面板数据的离散型因变量模型研究工作中，大多采用这一方法。

在我们设定的基本框架中，假定α和β并不随着个体或时期的不同而产生相应的变化。Xit包括了影响等级结果的所有可测因素。εit是模型的随机误差项，代表了那些无法观测的随机因素。εit服从logit分布，相互之间独立；εit和Xit之间也相互独立。然而在现实中，独立性假设无法保证。在企业经营方面，每年都有相同的因素（比如宏观经济背景）对各个企业产生影响。

在上文的模型中，我们假定自变量的斜率βk是固定不变的，同时假定不同残差εit之间相互独立。下面建立的随机效应模型考虑了随机系数的可能性，并根据现实情况放松了两个假定条件：一是βk不再是恒定不变的，它将具有时间效应，在不同时期自变量变化对因变量的影响程度将不再维持不变；二是我们把εit分为两个部分ζt和ξit，ζt代表了模型截距项的随机性，因此截距项不再是一个固定的值，它同样具有时间效应，将随着t的不同而变化，ξit则依然表示不同个体不同时期的不可测因素。即模型变化为：

模型参数βk是衡量发生比比率OR①的参数。在扩展模型中，所有自变量X分成了两部分：Z是那些因为时期不同而将产生不同影响的自变量，X＊代表了效应恒定的自变量。λt描述了带来时期差异影响的自变量对发生比比率的影响程度，也就是自变量Z的斜率的随机部分；β2表示那些并不随时间变化而改变的斜率。我们假定λt的条件期望E（λt｜Xit）为0，条件方差var（λt｜Xit）为ψt，这说明λt围绕0以的幅度波动，也就是表示当斜率有时间随机效应时，斜率将在范围内变化；ζt的条件期望E（ζt｜Xit）为0，条件方差var（ζt｜Xit）为φt，这说明截距项围绕α在的幅度内上下波动。同时假设ξit之间相互独立，ζt、ξit和Xit之间也分别相互独立。我们还必须对λt进行假定：λt和ζt、ξit、Xit分别相互独立；λt之间也相互独立。另外一个重要的假设是模型中的随机截距项和随机系数符合期望值为0的联合正态分布。

统计推断的原假设为H0∶OR＝exp（βk）＝1。这一原假设等同于H0∶βk＝0。和连续型线性模型一样，Wald检验和Z检验都可以用来对βk进行统计推断。

这样，带有随机效应的排序模型就把解释变量未能解释出来而实际上对个体有着不同影响的因素分离了出来。

三、含随机效应排序响应面板数据模型在银行信用评级领域的运用

由于整个信用评估系统复杂繁琐，在一篇论文中无法将其全部包括。从历史来看，绝大部分的研究工作都是致力于企业财务状况因素的分析。因此，本文也重点关注此方面。

本文以我国某大型国有控股商业银行为例进行实证分析，其是中国较早开始进行贷款申请客户信用评级工作的银行之一。该银行以企业评级标准值和不允许值为基础，对贷款申请客户进行客观、公正、科学地分析和判断。该行将客户信用等级划分为12个级别，分别为AAA级、AA级（AA＋、AA、AA－）、A级（A＋、A、A－），BBB级（BBB＋、BBB、BBB－）、BB级、B级。本文选取的数据是236家制造业中等规模企业②2005～2008年连续向该商业银行提出贷款申请时提交的企业相关财务信息③。由于该银行规定客户提出贷款申请时必须提供近三年的财务报告，同时银行也会根据历史数据对申请贷款的客户进行过往三年的信用等级评估，因此我们实际获得的数据包含了2003～2008年间的相关信息。在部分年份某些企业不能提供某些指标的有效信息，即存在数据缺失问题。

能够反映公司经营状况的财务指标非常多。Chen和Shimerda指出在大量的文献中有超过100个财务比率用于分析企业经营状况，其中大约50%至少在一项研究中被证实是显著的［6］。因此，要进行企业信用等级评定的有效研究，小心选择财务比率是至关重要的。本文根据财务比率的特点将全部财务比率分为四类：偿债能力状况比率、财务效益比率、发展能力比率和资产营运状况比率，具体所用财务比率见表1。

表1 模型所用财务比率

我们分别建立“伪面板数据”模型（模型一）和含随机效应的面板数据模型（模型二）。通过两个模型的比较，判断哪个模型能更好地对现有评级系统进行检验。模型的解释变量是各个财务比率，被解释变量是贷款申请客户得到的信用等级结果。在样本中没有出现信用等级为BB级、B级的情况，所以进入模型的信用等级一共是10级，模型设定的排序为10类等级排列，被解释变量的取值范围是“1，2，…，10”，依次代表 AAA、AA＋、AA、AA－、A＋、A、A－、BBB＋、BBB、BBB－。用 GLLAMM程序经过前向逐步回归调整模型后，发现无论是否考虑随机效应，模型估计结果都发生了很大变化。在两个模型中，资产负债率、流动比率、主营业务利润率、流动资产周转率、资本积累率、全部资本化比率、经营活动产生的净现金流量／总债务、成本费用利润率8个财务比率在统计上都表现出了显著性。模型二中，资产负债率、流动比率、主营业务利润率、流动资产周转率、资本积累率5个财务比率的系数表现出了随机性。经过模型调整，得到估计结果如表2所示。

我们用这两个模型进行预测估计，分别得到各个贷款申请客户获得不同等级的概率值pr（i）。期望等级是各个贷款申请客户信用等级的预测期望值，其计算公式为将期望等级与原等级相减，即可得到模型的预测误差。由于部分观测对象含有某些财务指标的缺失值，所以在模型预测时需要将这些观测对象剔除。最终，我们得到1 229个合格的预测对象，统计结果见表3。

为了更清晰地对两个模型的预测能力进行比较，列出了预测误差分布图（图1）。图1中，柱形图代表模型一的预测误差分布，而折线表示模型二的预测误差分布。横坐标表示模型预测期望等级和原银行评级系统所得等级结果的误差，纵坐标表示落入各个误差级别中的观察对象个数。

表2 含有／不含有随机效应的排序响应面板数据模型估计结果

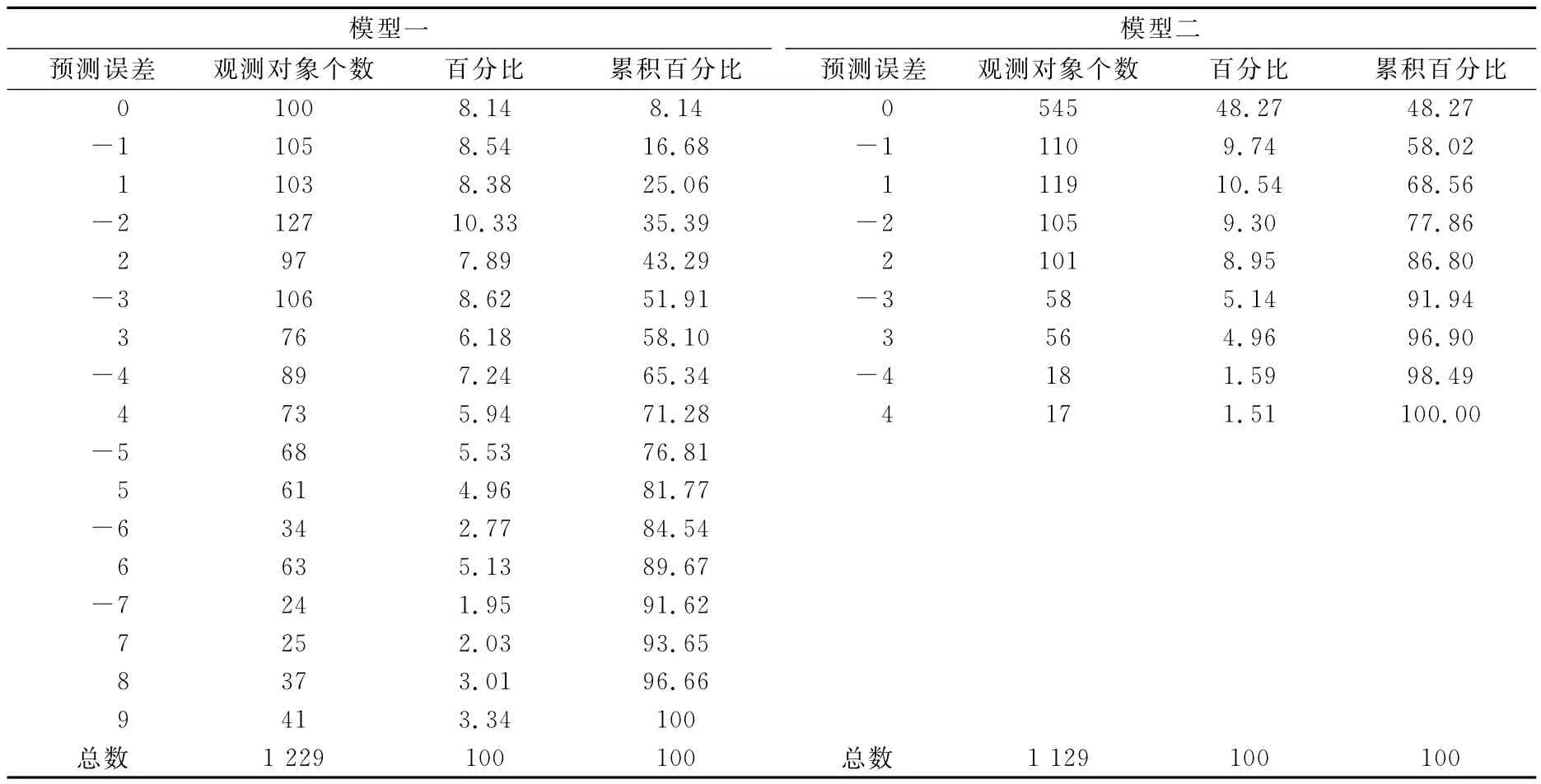
表3 模型预测误差统计

图1 模型预测误差分布图

针对模型所进行的全样本预测估计，实际上是对模型拟合度的检验。比较两个模型的结果发现，即便模型参数估计值差别并不大，其预测结果也是迥然不同的。对模型二而言，模型预测完全正确率为48．27%，而预测等级误差在两个等级之内的百分比达到86．8%。多元分类的预测正确率较二元分类模型要低得多④，本文采用的是10个类别的排序响应模型，因此模型二的预测效果是相当理想的，这也表明了模型二对现实情况的拟合程度相当高。

模型一的预测效果明显弱于模型二。首先，模型一的预测正确率大大低于模型二。通过表3可以看到模型一的预测完全正确率仅仅为8．14%，预测误差在两个等级之内的比率也只达到了43．29%。这样低的预测正确率说明该模型不能理想地拟合原银行评级系统，因此无法实现对原有系统的检验工作。其次，图1显示，模型二的预测误差分布图类似正态分布，左右对称，但是呈现“尖峰厚尾”特征，其最大误差等级控制在四级之内。这说明含有随机效应时，模型的预测误差是能够被有效控制的，且误差分布均匀对称。而不含有随机效应时，模型预测误差分散，最大等级误差达到了九级之多，误差分布有左偏现象，预测等级结果更偏向于低类别等级，因此模型更倾向于高估企业信用水平。

我们可以确定，由于考虑了数据的时间效应，在模型中增加了随机效应，预测能力得到了极大提高，因此模型二适合用来对现有信用评级系统进行进一步检验分析。

四、检验结果分析

第一，根据模型二的估计结果，即使进行信用等级评级的财务比率减少到8个，模型仍然能够很好地拟合原有的信用评级结果。这说明了原有信用评级系统存在冗余指标。这些冗余指标造成了多重共线性，直接影响了信用评级模型的估计结果和预测能力。

第二，我们发现估计结果中资产负债率和全部资本化比率两个指标对应的OR值超过了1，其中资产负债率对应的OR值为11．837，全部资本化比率对应的OR值为2．901。其余财务指标对应的OR值均小于1。这说明资产负债率和全部资本化比率对信用等级起到了正向的作用，资产负债率越高，企业所对应的信用评级也就越高，信用质量就越差。全部资本化比率也是同理。

第三，我们进一步发现，成本费用利润率对应的OR值相当小，仅为0．001。这说明成本费用利润率虽然在统计上显著，但是模型分析结果显示，它对信用等级的影响程度相当微小。同时，在现有评级系统中，该财务比率对应的权重设置也相当小，仅为0．02，这表明该财务比率在现有评级系统中没有被视为一个特别重要的指标；另一方面，从原始数据来看，对于各个观测对象，该财务比率的波动非常小，说明该比率不能很好地区分出各个观察对象的信用等级。因此，我们可以判断，成本费用利润率虽然在统计上显著，但确实是一个冗余指标，可以将其剔除出现有评级系统。

第四，根据该银行信用评级方法的规定，原信用等级评级系统中，各个财务比率所对应的权重大小排列顺序依次为：资产负债率、主营业务利润率、流动资产周转率、流动比率、资本积累率、经营活动产生的净现金流量／总债务、全部资本化比率、成本费用利润率。而通过模型，我们可以看到实际上各个财务比率对信用等级影响程度的绝对值排列顺序并不完全和事先设定的一致，其顺序依次为：资产负债率、全部资本化比率、流动比率、资本积累率、流动资产周转率、经营活动产生的净现金流量／总债务、主营业务利润率、成本费用利润率。因此，我们可以根据模型检验结果，在保证原有指标相对重要性顺序的前提下，对原有评级系统的权重设置进行相应修正，以便更科学合理地进行信用评级工作。例如，在现有评级系统中，主营业务利润率被视为第二重要的财务比率，而模型结果显示其影响程度远远不够，这意味着系统原来设定的权重并不足以反映其重要性，应加大其对应的权重设置，以增强它的影响力。

第五，含有随机效应的排序响应面板数据模型的一个重要特征是在模型中不仅考虑了某一时点上不同企业的财务状况，更重要的是它还综合考虑了同一企业在不同时点上的财务变化情况和信用等级变化情况。在考虑不同时点对各个企业共同作用的宏观经济因素时间效应后，模型能够从横截面和时间序列两个方面，更完整地描述银行信用评级系统的统计计量特征，从而更合理地对现有评级系统进行合理性检验。

五、总结

本文将面板数据模型和排序响应模型结合起来，建立了一个考虑时间效应的随机效应模型，将其运用在银行信用评级系统检验工作中。这一模型能够对贷款申请企业在随后若干年的信用等级变化情况进行初步评估，为银行授信工作提供更科学客观的佐证。这一方法克服了现有评价方法的不足，同时保留了logit模型便于操作和容易进行经济解释的优点，便于模型的检验和使用，因此具有很强的理论意义和实践意义。实证分析的结果表明，这一方法能够科学合理地对银行现有评级系统进行检验，为银行修正评级系统提供重要依据，并且能够对贷款申请进行初步评级，提供更为客观的信用等级结果，从而提高银行贷款的质量，提高商业银行管理和分配资金的效率。

注释：

①发生比比率OR指发生比Odd（yit＞s｜Xit）在xkit发生变化前后的值的比率。

②该银行对贷款客户企业规模大小和行业分类的划分标准是在国家2003年颁布的《国家经济贸易委员会、国家发展计划委员会、财政部、国家统计局关于印发中小企业标准暂行规定的通知》和1988年颁布的《大中小型工业企业划分标准》的基础上进行调整后制定的。

③因为涉及银行内部核心机密，本人承诺不以任何形式披露相关具体数据及敏感内容，但是这并不妨碍本文的思想和技术介绍。

④Huang等指出评价模型预测效果应该根据信用等级数进行调整，他们指出分类超过5级的分级模型，其预测正确率应该在55%～75%之间［7］。

［1］王恒，沈利生．客户信用评级系统的经济计量模型检验［J］．数量经济技术经济研究，2006，（6）：138－147．

［2］Tucker，J．Neural Networks versus Logistic Regression in Financial Modeling：A Methodological Comparison［Z］．Paper Published in Proceedings of the 1996 World First Online Workshop on Soft Computing（WSC1），Nagoya U－niversity，1996．

［3］Ronghua，Hansheng．A Composite Logistic Regression Approach for Ordinal Panel Data Regression［J］．International Journal of Data Analysis Techniques and Strategies，2008，1（1）：29－43．

［4］Rabe－Hesketha，S．，Skrondal，A．，Pickles，A．Maximum Likelihood Estimation of Limited and Discrete Dependent Variable Models with Nested Random Effects［J］．Journal of Econometrics，2005，128（2）：301－323

［5］Skrondal，A．，Rabe－Hesketh，S．Prediction in Multilevel Generalized Linear Models［J］．Journal of the Royal Statistical Society：Series A（Statistics in Society），2009，172（3）：659－687．

［6］Chen，K．H．，Shimerda，T．A．An Empirical Analysis of Useful Financial Ratios［J］．Financial Management，1981，10（1）：51－60．

［7］Huang，Z．，Chen，H．，Hsu，C．－J．，Chen，W．－H．，Wu，S．Credit Rating Analysis with Support Vector Machines and Neural Networks：A Market Comparative Study［J］．Decision Support Systems，2004，37（4）：543－558．

（责任编辑：易会文）

F224

A

1003－5230（2011）01－0062－07

2010－10－28

福建省数量经济学研究生教育创新基地资助

郑大川（1977— ），男，福建龙岩人，华侨大学经济与金融学院博士生；

沈利生（1946— ），男，北京人，华侨大学数量经济与技术经济研究院教授，博士生导师，中国社会科学院数量经济与技术经济研究所研究员，博士生导师；

黄 震（1955— ），男，福建莆田人，美国奥特本大学数学科学系教授。