供应链管理的激励资金博弈供给与分配

黎 明 （湖南现代物流职业技术学院，湖南 长沙 410131）

·供应链·

供应链管理的激励资金博弈供给与分配

黎 明 （湖南现代物流职业技术学院，湖南 长沙 410131）

供应链生产运行方式是以核心企业仅保持其核心技术和创新信息的制造或者经营资源，把其它业务外包给另外合作企业，链合供应商、生产企业、销售商而建立的一条商品生产网链[1]，每一个企业就是一个链点，相邻链点之间是一个需求与供应关系，故称之为供应链。图1为供应链点企业结构图。

在供应链环境下，各链点企业的利益都不应被忽视。但由于：第一，多条供应链间的激烈竞争，多表现在产品市场价格战，这就把销售成本压向供应链基础环节，挤压了弱势的企业利润空间。第二，供应链内部企业以签订合同相链合，各企业的收益和成本均由合同决定，无发言权的企业无法与核心企业相抗衡，因而供应链优化而产生的额外收益没有惠及基础企业，这会造成供应链的不稳定。稳定的供应链管理应以激励金的方式来均衡链点企业的利益，保证各链点都有合理的利润空间，以利于此供应链的巩固与发展。故激励金是供应链产业的完善剂和稳衡器。稳定的供应链内激励金是如何提供？如何分配？可按博弈论中 “公共物品私人自愿供给”的模型来模拟激励资金的供给问题。

1 激励资金的供给问题

设想一个由n个链点企业组成的一条供应、生产、销售的供应链，需要建立—激励资金库来完善，稳定并能使之增值。第i链点企业自愿供给激励金数gi，则激励金总额假设激励金机制使i产生的效用函数为ui=（xi,G ），反映i企业在激励机制中获得的利益函数，这里xi是订单激励的订单产品数。令pxi为订单产品的成本，pGi为单位投资成本，Mi为i企业的总收入。则i的最优战略 （xi,gi）以最大化目标函数Li，（λ为任意参数）：

最优化的一阶条件为：

供应链内最低约束条件为：

α,β是反映激励机制中订单与激励金的激励绩效的数值。

则：

由 （2）、 （3）、 （5）可得i企业提供的纳什均衡条件下的最优决策激励金：

激励金的博弈供给公式 （6）可以如下讨论：

1.1 供应链生产中获利Mi越大的链点企业 （核心企业），应提供更多的激励金。这比较好理解。如一小乡村集资修条好路，出资多的总是富户，穷户只是出极少资金。因为修好路对富户收益更多。供应链内各企业也是如此，此产业链越稳固，越完善，核心企业也就越能获利，当然收益多的企业也应多供给激励金。

1.2 在供应链生产中投资成本 （pGi）越小的链点企业需多提供激励金。pGi值大意味着在此供应链内是最重要、最薄弱的环节，是关键点处，尤其需多加重视。

1.3 （6）式等式右边的第二项表明，如同自然人一样，各链点企业存在 “心理意度”问题。假若其他企业提供的激励金多，则自己可以减少供给量。所以在激励金的提供过程中，应公开化和透明化。

激励金激励G的指数β值大，表明激励金激发了供应链内部所有企业的积极性，使所有企业都有激励效用。若α相对β值小到可以忽略，即α→0，这表明激励金效用达到极值。此时，供应链激励金的博弈纳什均衡供给就变为帕累托最优供给方式，这是最佳激励手段。

2 激励金的分配原则

激励金的分配要达到1.4中效应函数极大的原则，在实际中有两种方案可供参考。

2.1 激励金的供应链增值量分配法。由传统管理方式向供应链管理方式转变后，制造商的增值作用降低了。供应链的增值点发生的转移。图2是此过程的示意图。

因此，激励金应向增值效应高的两端即供应端和销售端分配倾斜，即 “重两头轻中间”。加大供应环节的激励力度，以保持供应链源头的高质量和高品位；加大供应环节的激励力度，以期扩大市场占有率，现实利润的获得与增加。

激励机制的管理经验来进行激励金分配，再加上订单激励；商誉激励；信息激励；淘汰激励；新产品/新技术开发激励；组织激励等手段，使得各企业的激励效用增大，使供应链运作更加顺畅，实现供应链企业共赢的目标。

2.2 激励金的博弈分配法。激励金的博弈分配与激励金的博弈供给为反比关系。

设Gi为i企业获得的激励金数，则有：

即供应链中收益越大，投资成本越低的企业提供的激励金gi越大，而获得的激励金Gi越少。

以河北石家庄三鹿奶制品 （简称三鹿）的供应链为例，证明激励金供给和分配是关系核心企业存亡的大问题。

三鹿虽形成了完整的供应链生产运作，但没有合理的产业链利润分配机制和风险共担机制，奶农 （奶站）、乳企、销售超市是三个利益体，奶农作为整个链条的基础没有发言权，原奶采购价格由乳企或者乳企与当地政府协商而制定，通过奶站实施。从整个产业链分析[3]，奶源供应环节的投入应约占整个奶业产业的70%，加工环节占20%，流通环节为10%，即：

从收益分配来看，其收益比例为1∶3.5∶5.5，即：

可见，奶制品供应链奶牛养殖链点的投入与收益分配严重倒置，这是导致乳制品质量安全问题的根本原因。其结果导致整个产业链断裂，三鹿宣布破产，奶农、奶站及销售超市都受到严重损失。

假设奶供应、奶加工与奶制品销售这三大块组成的供应链以 （8）、 （9）式模型运行，那么为维护此条供应链正常，稳定进行，作为合理利润调节剂的激励金的博弈供给和分配比例应如下比例关系：

设pG3=n，则pG2=2n，pG1=7n；设M1=m，则M2=3.5m，M3=5.5m，代人 （6）式，可得满足纳什均衡条件方程组：

仅讨论α趋向零时供给趋向帕累托最优水平情况：

即：

而激励金的博弈分配比例如下：

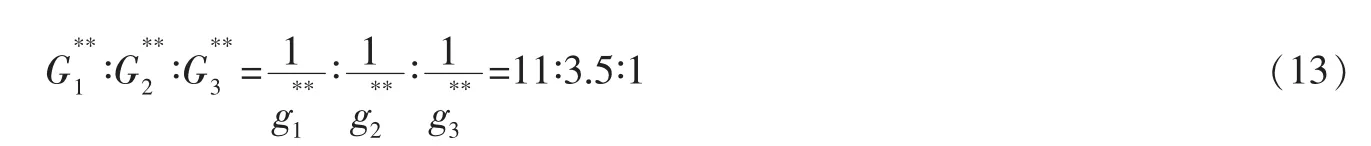
据CBN[4]记者报道， “每头牛每天要吃一捆干草需9元多，吃10多公斤饲料20元多。这样，饲草成本每天达30元。每年每头牛看病费用平均达几百元。而每头牛每天平均产奶20公斤左右，时下锡林浩特原奶价每公斤2.30元，实际上所赚无几。”激励金要使奶农户提供合格原奶的价格能在每公斤2.5元左右，确保奶农的利润，才能保证奶源的质量。销售环节要多让利给奶农；作为核心企业的乳制品加工公司则应以激励金发放形式，激励提供优质原奶的奶站和奶农。三鹿把主要资金花在了除加工设备外的市场营销和政府攻关上， “三聚氰胺事件”必然会爆发。忽视奶农利益，最终导致自身的覆灭。

稳定供应链管理中，激励金的供给和分配是极重要的管理环节。

[1] 马士华，林勇.供应链管理[M].北京：机械工业出版社，2008.

[2] 张维迎.博弈论与信息经济学[M].上海：上海人民出版社，2004.

[3] 赵剑峰.中国奶业结构—行为—绩效研究[D].北京：中国农业大学，2004.

[4] 华鹤良.奶业产业化经营中影响农民决策行为因素的实证研究[D].北京：中国农业大学,2004.

The Supply Chain Manages Incentive Funds Gambling Supplies and Assignment

LI Ming (Hunan Modern Logistics Occupation Technical College,Changsha 410131,China)

供应链管理中激励金的供给和分配是均衡链内各企业的利益空间，确保供应链得以稳固和完善。激励金效用函数ui=（xi,G ），可用博弈论中纳什均衡条件及预算约束方程求得各企业应供给的最优决策激励金额）及可分配的激励金总额（G*），激励金的博弈分配额度与供应量成反比关系。以石家庄三鹿乳制品集团案为例，计算了激励金博弈供给和分配的比例关系。

供应链管理；激励金的供给与分配；博弈纳什均衡

In the supply chain management,supply and distribution of incentive funds is balanced the interests of enterprises within the chain of space,to ensure that the supply chain can be a solid and improved.Incentive funds utility function ui=（xi,G ）,using game theory,Nash equilibrium conditions and budget constraint equations obtained by the optimal decision supply of various enterprises the incentive funds）and may assign incentive funds（G*）,the allocation of incentive funds game inverse relationship between amount and supply.Take Shijiazhuang's Sanlu Group dairy case as an example,has calculated the incentive funds gambling theory supplies and the assignment proportional relationship.

the supply chain management;supply and distribution of incentive funds;the game of Nash equilibrium

F273.7

A

2010-12-06

黎 明（1973-），男，湖南长沙人，湖南现代物流职业技术学院，讲师，经济师，研究方向：公交管理。

1002-3100(2011)03-0106-03