动态网络下多源多汇应急疏散问题算法

李金华 （华南师范大学 经济与管理学院，广东 广州 510006）

·产经研究·

动态网络下多源多汇应急疏散问题算法

李金华 （华南师范大学 经济与管理学院，广东 广州 510006）

在各种突发事件如火灾、地震、洪水、毒气泄露、恐怖活动等发生时或发生前，对人群进行应急疏散是减少生命财产损失的必不可少的应急措施，而疏散方案的及时制定是人群应急疏散的一个关键。

Hamacher和Tjandra[1]对疏散问题的数学模型进行了综述，将疏散模型分为宏观模型与微观模型两类。宏观模型强调对人群的建模，包括最小费用动态流、最大动态流、持续最大流、最快路与最快流等模型；微观模型强调对人群中的个体的建模，可以刻画个体特性及个体间交互对其行为的影响，包括社会力模型、元胞自动机模型、概率模型等。Gupta和Yadav[2]设计了基于网络优化理论的SAFE-R算法，用基于离散时间的动态流表示不同时刻疏散人员在各弧上的移动，动态的计算每条弧的实时流量。Lu、George和Shekhar[3]考虑多源多汇疏散网络的动态容量约束，将动态容量约束用时间序列方式进行描述，并给出了CCRP求解算法。Chen和Feng[4]提出了一种快速流控制算法应用于大型室内场所的应急疏散，可提高求解的速度。张江华等[5]研究了考虑存在有限顺序的多源点和容量限制下的应急疏散问题。

在各种突发事件发生时，往往很多事前确定的因素如路况、人流、资源可能会发生变化，人群疏散具有多源多汇、网络时变等特征，尤其是疏散网络的节点与边的容量可能是时变的 （或时间依赖的），如某道路或场所在某时段被堵，后又被疏通。离散的宏观模型往往采用时间扩展图 （time expanded graph,TEG）处理疏散网络的时变情况，这种方法具有较强的通用性，但是扩大了模型的计算复杂性，只能适用于一些中等规模的网络问题。文献[6-7]提出了一类表示离散时变网络的时间集合图（time aggregated graph,TAG），TAG比TEG更能节省存储空间，并且具有更高的计算效率，但是在求解精度上有所降低。

广东地处于珠江下游河网地区，船闸主要分布在上游北江和东江航道上。随着北江航道扩能升级工程的推进，清远枢纽二线船闸、飞来峡枢纽二三线船闸、白石窑枢纽二线船闸等由交通运输部门投资改扩建和新建的多线船闸也将陆续建成投入使用，如何协调与原枢纽船闸业主的关系、解决多线多梯级船闸联合调度的难题也迫在眉睫。为了推动船闸规范管理，2017年，广东省交通运输厅专门组织开展了《广东省船闸通航规范管理体制方案》研究工作，参照广西所采取的“三统一分”的船闸委托代管模式，结合广东实际，研究提出以北江为试点，将北江全线船闸由广东省航道事务中心统一管理，实现北江多线多梯级船闸联合调度。

一些研究如[2,4]将网络节点与边在最大容量限制下的动态流作为动态网络，这种对动态网络的认识存在着局限，有的研究如[5]虽然建立了时变条件下的数学模型，但是设计的求解算法只能适用于非时变情况，有的研究如[3]的算法存在许多的疏漏。本文借鉴TAG的思想提出了一个依赖容量约束的动态网络下多源多汇的人群应急疏散问题，设计了可根据路况变化即时输出疏散计划的启发式求解算法。

1 问题描述

1.1 问题假设

对于突发事件时的动态疏散网络，很多的时变因素可以通过时间依赖容量约束间接地反映出来，比如因边拥堵而导致旅行时间延长，可以转换为该时段边的容量降低甚至降为0，容量减少会引起边上的人流疏散产生拥堵。为此，本文仅考虑疏散网络上节点与边的容量约束是时间依赖的情况。

为了便于下面的建模，对研究问题提出如下假定：

（1）网络中每条边上的旅行时间为常数。

（2）网络中边和节点 （除汇点外）有容量限制，容量时间依赖，并且时变规律可知，但是不考虑节点容量时变对节点中已有人群的影响。

（3）边上的旅行满足先进先出 （FIFO）的原则。

时间过得真快呀！林强信扳着指头说，景花厂撑了七年，七年啊，居然在老子的围追堵截下存活了七年。七年之痒，哈哈，想想阿花这小娘们也不容易。林强信像公鸭似的嘎嘎大笑。

（4）疏散过程中只允许交叉节点有延迟，即边上的旅行是顺畅的。

（5）疏散过程中不允许返回和绕圈现象出现。

（6）网络中流量满足流量守恒规则。

下面介绍求最早到达时间路径的标号算法。节点vi标号用 （前驱节点pi，到达时间）表示，Q表示待处理节点的优先队列。具体算法如下：

（7）时间按离散时间单元来计。

1.2 符号与变量

（1）在所有的路径中R具有最早到达时间。最早到达时间的路径按下文提出的标号算法求取，人群按照该路径疏散所需的疏散时间最短。

GT=（V,E,T,TT,Cv,Ce ）： 表示动态疏散网络

V=｛vi| i∈[1,n]｝是节点集，n为网络总的节点数

E=｛eij|i,j∈V ｝是边集

T是疏散网络的疏散结束时间，疏散起始时刻设为0

TT=｛ttij｜（i,j）∈E ｝： 通过边eij的旅行时间

Cv=｛cvi（t）|i∈V,t∈ [1,T ]｝是时间依赖的节点容量集， 其中汇点容量为 ∞

Ce=｛ceij（t）|（i,j ）∈E,t∈ [1,T]｝是时间依赖的边容量集，由于每一条边的通过能力取决于通过该边的旅行时段内的最小边容量， 所以某时刻的容量取该旅行时段边的最小容量， 即ceij（t）=min｛ ceij（t'）:t'=t,t+1,…,t+ttij｝

S=｛si｜ i∈ [1,a]｝： 源点集S⊂V

vd：设置的超级汇点，与D中所有的点相连，并设超级汇点的容量为∞，与其相连的各边的旅行时间为0、容量为∞

D=｛di| i∈[1,b]｝： 汇点集D⊂V

本文算法允许人群在节点等待，路径中的节点具有到达时间与出发时间两个标识，最早到达时间的路径及时刻表的求取算法参考了TAG网络的最短路思想，能够适应时间依赖网络。由于多源点多汇问题复杂度高，故设置一个与各汇点相连的超级汇点，这在上文中已表述。再设置一个超级源点与所有的源点相连，设超级源点的容量为∞，与其相连的各边的旅行时间为0、容量为∞。这样就将多源点多汇问题转化为单源单汇问题。对各源点的待疏散人群采取分组疏散，每次迭代找到一条满足时变容量约束的网络最早到达时间的路径及时刻表，并得到该路径在疏散时段的最小容量，网络为人数为最小容量的该批次疏散保留容量，按照得出的时刻表及路径疏散出人数为最小容量的一组人群。反复迭代，直到所有源点的人群疏散完毕，即可得到各源点的分组数量、每组人数、疏散时刻表。

进水流道模型试验水力损失的测试结果如表1所示。由于相似准则采用了λΔp=1。因此，换算至原型设计流量及最大、最小流量时的流道水力损失与模型试验结果一致，列于表2。试验结果表明，肘形进水流道水力损失与流量的平方接近于成正比关系。在实型流道最大流量工况，即Qmax=30.39m3/s时，水力损失为0.059m，水力性能良好。

S（i）=｛si（i,j）∈E ｝：vi的后继节点集合

完成了数据库的连接以及各功能模块的设计后，需要进行包括工程项目管理、员工账号管理、基本权限管理以及人事信息管理等模块的软件设计。在这项设计中，最关键的是各模块的功能设计和界面设计。在功能设计方面，必须全面细致，因为它会影响整个ERP系统的结构。在连接数据库时，可以使用ODBC数据源对其进行设置，或者使用Web.config文件编写数据库。

2 算法设计

2.1 基本思路

文献[3]提出了分组思想，但是存在较大的不足： （1）该文献需要假定边的旅行时间包含了在交叉路口 （即节点）的等待时间，这在实际应用中难以实现； （2）由于该假定的存在，文献中算法的核心部分即最短路算法采用了一般化的Dijkstra算法，这难以适应对时间依赖网络的处理，可能导致求出的结果偏差过大。例如，一个显著的问题是：在某时刻、某节点，如果算法判断从该节点发出的某条边不满足可用容量大于0的条件，算法就会放弃该支路，而很有可能的情况是在该节点经过等待延迟后该支路仍可能是最短路。

Q=｛qi| i∈[1,a ]｝： 各源点待疏散的初始人数集和， 总人数为q

P（i）=｛pj｜（j,i）∈E ｝：vi的前驱节点集合

(4)内网计算机与外部交换数据，应由专职资料员负责，数据载体要在中间机上杀毒后才能交换数据，数据进出有登记。

2.2 求解方法

Input：

近期公布的这一序列，涵盖了94%的基因组（更早的版本为61%），更有助于将特定的性状与特定的基因联系起来，从而着手对其调整。

（1） 网络 GT=（V,E,T,TT,Cv,Ce ），包括节点及边、最大疏散时长，各边所需的旅行时间、各节点的时间依赖容量、各边的时间依赖容量。

（2）源点S、汇点D以及初始时刻各源点的待疏散人数。

（3）初始疏散时刻为0。

为了便于检测和防止滑移而引起漏播，充种带采用同步带，根据带轮和设计需求，带宽25mm。由于同步带较薄仅能满足传送需求，无法形成足够大的型孔以充种。所以，需要在带上粘覆一层软橡胶材料，以便做出型孔。带长370mm，设计型孔两排，每排37孔。同步带上每孔直径为2mm，以便检测，且种子不会漏出，如图4所示。

消费者团体也对如何标记基因编辑食品提出了警告。虽然美国国会通过了一项法律，要求食品制造商自2016年起需要明确标识食品的转基因成分，但是这些规定可能不适用于通过基因编辑技术新近上市的食品。

Output：

疏散方案：各源点的分组数量与每组人数、各组的疏散线路及时刻表、网络出清所需的疏散时间。

Method：

Step1：添加超级源点vs与超级汇点vd到网络G及GT，并设vs、vd的容量为∞，与其相连的各边的旅行时间为0、容量为∞。

Step2：检查任何源点si∈S中是否存在待疏散人群，如果存在则执行下列子步骤Step2-1～2-3，否则跳转到Step3。

Step2-1： 寻找 vs到 vd的路径 R=｛vs,v0,v1,…,vk,vd｜v0∈S,vk∈D ｝，R具有时刻表其中表示vk的到达时间，表示vk的出发时间，并且R满足条件：

G=（V,E ）： 表示静态疏散网络

12月1日，全国第六届“书香三八”读书活动颁奖典礼暨第七届“书香三八”读书活动启动仪式在北京举办。全国总工会女职工部领导参加颁奖典礼并致辞。兵团工会在第六届“书香三八”读书活动中，荣获优秀组织奖。

（2）R各边的可用容量available_cei（i+1）,∀i∈ ｛0,1,…,k-1 ｝。

（3）R各节点的可用容量available_cvi+1, ∀i∈ ｛0,1,…,k-1 ｝。

Step2-2：确定路径R的新增流量，fR=min（源点si的剩余人数，各边的可用容量，各节点的可用容量）。

Step2-3：对于所有的i=0,1,…,k-1，依次执行：

（2）available_cei（i+1）=available_cei（i+1

Step2-4：将R中的源点v0的待疏散人数减少fR，如果此源点的待疏散人群变为0，则将它与vs的连接边移除。跳转到Step2。

Step3：输出疏散方案。

文中涉及的记号与术语可参见[1,10-11]。若X是拓扑空间,F⊆X,F在X中的闭包记为clF,在涉及多个空间时,为区分起见也记作clXF。空间X的全体开集与全体闭集分别记为Ο(x)与Γ(x)。

Step1：初始时，节点vs的标号为（0,0），Q=｛vs｝，其他节点的到达时间为∞。

Step2：判断集合Q是否为空，如果为空则跳转至Step5，否则取出集合Q中最小的元素vi，并将它从Q中删除。

Step3： 对vi的后继点集合 ｛vj| j∈S（i ）｝中的所有元素， 循环执行如下操作：

Step4：跳转至Step2。

2.1 热水烫种消毒：先将蔬菜种子装入尼龙网袋中，再用30℃左右的温水浸种30分钟，促使种子上的病菌活化，这样容易杀死病菌。同时应不断搓洗，以洗掉种子上所带的抑制发芽的物质，而且也可使带茸毛（番茄）的种子湿透，以增加烫种效果。

Step5：根据标号从目的点回溯路径，得到最早到达时间的路径R。如果存在多条最早到达时间相同的路径，则选择流量最大的那条路径。

在数学教学过程中，加强课堂互动，必须讲究有效性，通过师生互动交流，教师能够充分发挥教育机制，能够在教学活动中对学生的各类表现以及意外情况、偶发事件进行及时反应，采取有效的措施解决问题。通过因势利导，结合学生的学习特点以及多元化需求、教材内容，引导学生进行思考探究，调动学生的兴趣，使学生扬长避短，通过循循善诱，切实提高课堂教学效率。在教学中，教师可以引导学生思考，通过举一反三，鼓励学生勇于质疑，切记不要采用包办代替的教学方式，如果仍然采用传统讲授式教学方式，学生只能够学习到相应的技能，而缺乏探究创新精神。

2.3 算法复杂性分析

本算法采用的是分组疏散的方法，每次迭代产生一个分组，那么迭代的次数在最糟糕的情况下等于待疏散人群的总人数q，即每次疏散1人，其计算复杂性为O（q ）。在每次迭代中需要寻找一次最早到达时间路径，上述标号算法的计算复杂性为O（n2），其中包含的一些子步骤的计算复杂性大致为O（n ），可以忽略。所以总的计算复杂性为O（q· n2），如果采用稀疏网络的最短路算法对最早到达时间路径算法进行优化，还可以将计算复杂性降为O（ q·nlogn ）。而在同样条件下，TEG动态网络疏散的线性规划算法的计算复杂性为其复杂性在一般情况下要远大于本算法，当然其结果是最优的。

科学技术的飞速发展使移动短视频平台更加方便地融入到了大众的生活之中，降低了内容生产的门槛，增加了用户对短视频平台的使用率，使用户可以随时随地分享生活，让更多的消费者有选择的空间。

3 应用分析

构造如图1所示的疏散网络图作为网络疏散场景。图中：vs为超级源点，vd为超级汇点，s1、s2为两个源点，除超级源点外两源点没有其它接入的边 （这样只是为了简化求解过程），源点的初始待疏散人数分别为20、30，d1、d2为两个汇点，边的上方标示的数值表示该边的旅行时间。初始时间为0，最大时间为30。

为简单起见，假设所有的边与节点 （除超级源点、超级汇点、源、汇点及与超级源点汇点所连的边外）的时间依赖容量约束满足同样的规律， 即为： ｛t=0～5:5;t=6～10:7;t=11～15:8;t=16～20:6;t=21～25:5;t=26～30:8 ｝。

为节省篇幅，各次分组计算的过程不详细展示，将各次的分组方案列成表1。两源点待疏散人群全部疏散完毕，疏散时长为15个时间单元。

4 结 论

时间依赖网络中的应急疏散问题具有一定的现实基础，然而对该问题的研究存在着一些不足，如对动态网络的认识存在着局限、基于TEG的疏散模型求解复杂性高等。扩大该问题的应用规模。降低该问题的计算复杂性具有较大的必要性。为此，本文提出了时间依赖容量约束的动态网络下多源多汇的人群应急疏散问题，基于分组疏散的思想和TAG时间依赖网络的最短路算法，设计了一个启发式求解算法，最后作了应用的算例分析。本算法具有思路简单、算法复杂性不高、解的满意度高的优点。

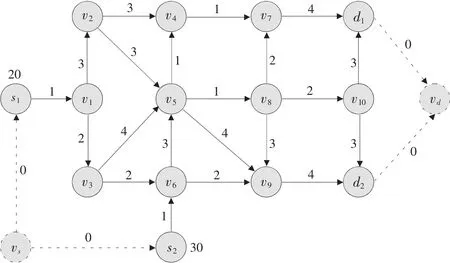
图1 疏散网络简图

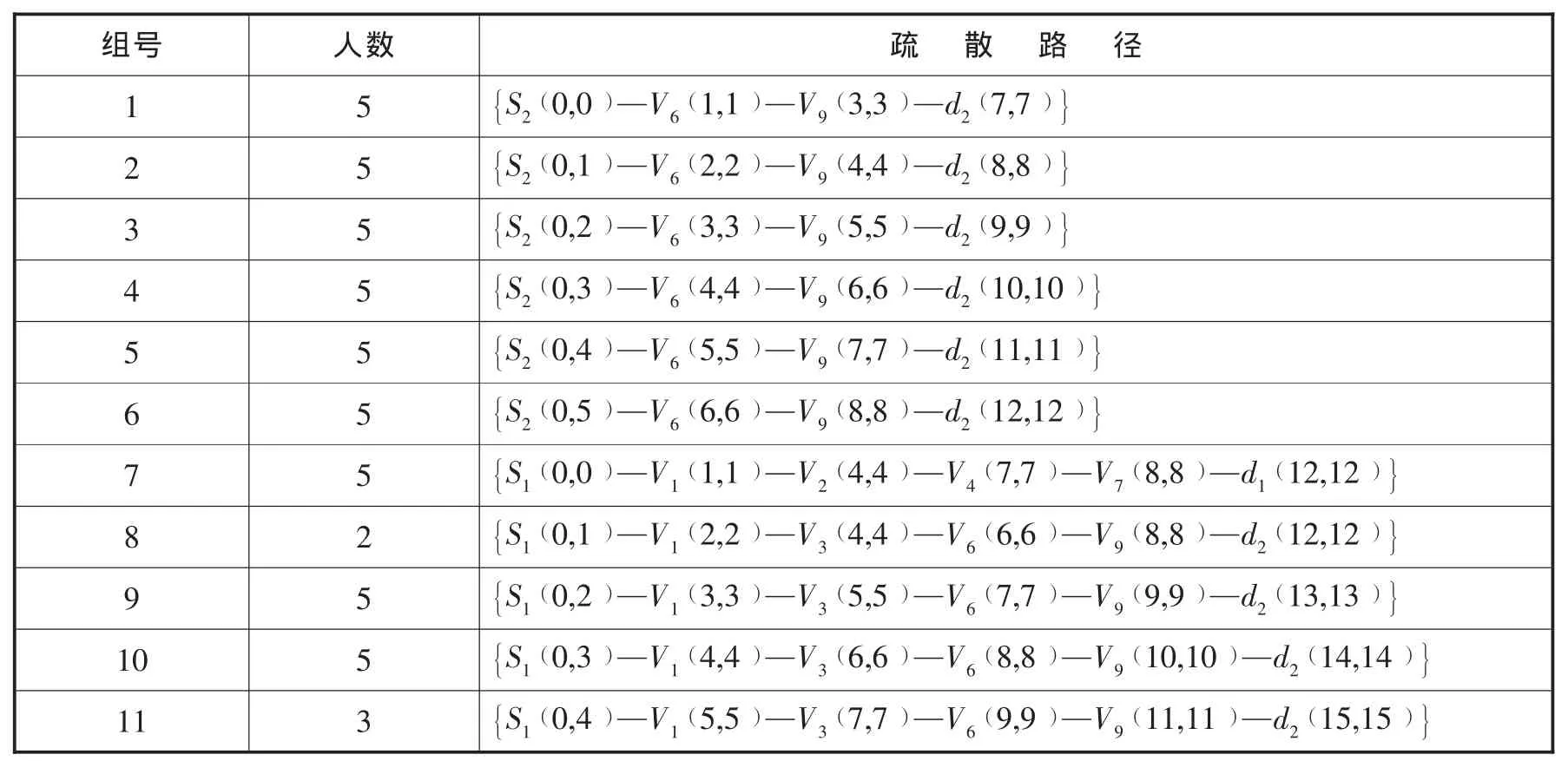
表1 分组方案列表

[1] Hamacher H W,Tjandra S A.Mathematical modeling of evacuation problems-a state of the art[M].Pedestrian and evacuation dynamics,Berlin:Springer-Verlag,2002.

[2] Gupta A K,Yadav P K.SAFE-R:a new model to study the evacuation profile of a building[J].Fire Safety Journal,2004,39(7):539-556.

[3] Lu Q S,George B and Shekhar S.Capacity Constrained Routing Algorithms for Evacuation Planning:A Summary of Results[C]//Advances in Spatial and Temporal Database Proceeding of 9th International Symposium on Spatial and Temporal Databases,Heidelberg:Springer Berlin,2005:291-307.

[4] Chen P,Feng F.A fast flow control algorithm for real-time emergency evacuation in large indoor areas[J].Fire Safety Journal,2009,44:732-740.

[5] 张江华，刘治平，朱道立.多源点突发灾害事故应急疏散模型与算法[J].管理科学学报，2009,12(3):111-118.

[6] George B,Kim S,Shekhar S.Spatio-Temporal Network Databases and Routing Algorithms:A Summary of Results[C]//Proceedings of International Symposium on Spatial and Temporal Databases （SSTD07）,2007.Berlin Heidelberg:Springer-Verlag,2007:460-477.

[7] George B,Shekhar S.Time aggregated graphs:a model for spatio-temporal network[J].Journal on Semantics of Data,2008,11:191-212.

The Algorithm of Multi-Source and Multi-Sink Emergency Evacuation Problem on Dynamic Networks

LI Jin-hua (School of Economics&Management,South China Normal University,Guangzhou 510006,China)

提出了一个时间依赖容量约束的动态网络下多源多汇的人群应急疏散问题，基于分组疏散的思想和TAG时间依赖网络的最短路算法，设计了一个启发式求解算法。算法将多源多汇问题转化为单源单汇问题，对各源点的待疏散人群采取分组疏散，并为每组人群找到一条满足时变容量约束的最早到达时间的路径及时刻表。最后进行了方法的应用分析。该算法能适用于大规模时变网络的人群应急疏散。

动态网络；应急疏散；分组；标号算法

This paper considers a multi-source and multi-sink emergencyevacuation problem on time-dependentcapacity constrained networks.Based on grouping evacuation idea and the shortest path algorithm on time aggregated graphs （TAG）,a heuristic algorithm is designed,which converts multi-source and multi-sink problem into single source and source sink problem,and takes grouping evacuation method.Each group is assigned the route with the earliest destination arrival time meeting time-dependent capacity constraint to evacuate.An example is demonstrated finally.The algorithm can be used to solve the emergency evacuation problem on large-scale timevariant networks.

dynamic networks;emergency evacuation;grouping;label method

TP202:U116.2

A

2011-01-12

李金华（1972-），男，湖北仙桃人，华南师范大学经济与管理学院，副教授，管理学博士，复旦大学管理学院博士后，研究方向：复杂系统理论与应用、物流管理。

1002-3100(2011)03-0136-04