基于鲁棒优化的多级多周期库存管理优化模型研究

刘宝兴，刘 亮，韩继方，许 波 （中国飞航技术研究院物资供应站，北京 100074）

·国防军工物流论坛专栏·

基于鲁棒优化的多级多周期库存管理优化模型研究

刘宝兴，刘 亮，韩继方，许 波 （中国飞航技术研究院物资供应站，北京 100074）

供应链管理建立在协同和共赢的信念基础之上，供应链成员在相互信任、互利及长期发展基础上，将最终消费者的需求转化为所有参与者的集体行动，每一个成员都在产品或服务的生产和提供过程中从事一部分活动，并且相互之间开展信息共享和合作行动，不但可以在相互支持、配合和协调中实现整体利益最大化，也会使每一个参与者从中获益。

1 假设与符号说明

本文选取串行链结构的供应链库存为研究对象，串行链结构如图1-1所示：

我们假设串行链是一个周期符合离散分布的动态系统，并用j表示供应链中级数，其中j=1,2,3,…,m；dt表示第m个节点企业面临的市场需求，其中t=1,2,3,…,n代表规划周期的期数[1-3]；至此，m和t分别为下一节将要建立的多级多周期库存模型的重要变量，供应链的级数由m体现，供应链的运行周期有t来体现，并且如无特例说明本文中提到的供应链级数都大于等于3，并且周期为10以上的周期数。我们定义初始的第j级供应链节点接受来自第j+1级节点的需求：＞0，而t时刻结束时第 j个节点企业的库存为，而每一个节点j的初始库存为，同时假设下一级对上一级节点的需求最终转化为在库存数量上各节点企业间传递；同时也假设在订单下达到订单完成存在非负的时间延迟[4-6]。在这里时间延迟分为3种：

（1）信息传递延迟：信息由下一级向上一级节点传递时发生的延迟，用I表示，且I为非负整数。

（2）生产延迟：订单完成直到订单完成或者某一节点企业组织好货源发生的时间延迟，用M表示，且M为非负整数。

（3）提前期：信息由市场需求开始直到传递到最上游节点发生的时间延迟，用L表示，且L为非负整数。

I m+（）1表示m级供应链接受来自市场需求的时间传递延迟，则库存关系一定满足下面的方程：

以上简单数学模型说明某级供应链在某周期发生的库存变化情况，这种变化就是原有库存减去市场需求的差额。当库存为负时，表示市场需求没有满足或者缺货。尽管缺货或者市场需求没有满足，但是库存在相邻节点企业间仍会连续传递，这种情况可以用 “借货”策略来解释，当某供应链无法满足 “市场需求”时，可以借用同标准同数量的货物来满足 “市场需求”，而“借货”可以随后补充给借方。这时自然会产生借货成本，同时也得假设在最终供应商之外有足够可借货源[7-10]。我们优化的目标为供应链总成本。总成本包括：

（1）购买或者生产成本，我们定义在t周期的j级供应链的每单位购买或者生产成本为，当规划周期t足够长的时候，我们必须考虑资金成本

（2）库存持有成本，在t周期的j级供应链的每单位货物的持有费用，我们定义为hjt；

（3）缺货成本，在t周期的j级供应链的每单位货物的缺货损失，我们定义为

2 模型建立及优化

2.1 模型建立及线性规划

如假设和定义规定的，系统动态的数量关系可以用方程 （1.1）表示，那么整个供应链的优化问题可以描述为如下的线性方程：

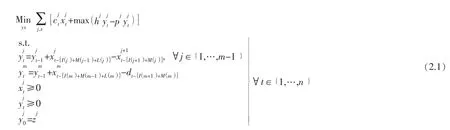
经观察发现，由于方程 （2.1）并非线性方程，所以需要把问题转化为线性问题 （Liner Programming,LP），我们替换目标函数中的max，这样方便我们引入辅助变量以简化问题，我们令TL（j）+I（j）+M（ j-1）+L（j）表示在j级供应链中订单下达直至到达的延迟，同时令TM（j）=I（ j+1）+M（j）表示订单从j级供应链节点到j+1级供应链节点的延迟。通过线性规划，我们可以把（2.1） 改造为：

2.2 鲁棒优化

现在采用广义鲁棒优化，假设dt和zj的正常范围分别为和定义式（2.3）中的标准为l1-标（）准 ，则线性规划系如下：

这里， μ2,t,j和为 “敏感参数” （先前用α表示），作为变量，为限制其变异，我们添加如下限制：

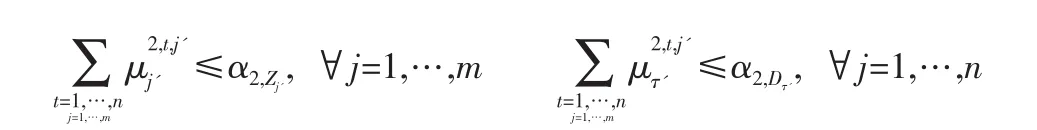
这一部分，我们用仿真方法来呈现由鲁棒优化得到的结果。为评价解决方案的优劣，我们选用 “乌托邦”方案作为基准[11]。对给定的虚拟需求轨迹和初始库存，乌托邦方案是相对应的线性系 （2.2）的决策方案。乌托邦最优值包含一个由最优控制得到的成本下限。本节所选用的特殊广义鲁棒优化可获得最低成本，是与α的上限 （一般由疏忽、错误操作所致）相对应的。我们将用几种不同的方法来检测不同虚拟需求下的解决方案的优劣性，其中两个重要方法为：成本最小法和偏差率法。偏差率其中，Ak是用A方案实现k的目标函数值，OPTk是实现目标的乌托邦方案值。

3 算例分析及仿真

正如前面章节所述，本优化方法的目的有二：系统稳定和总成本最小。下面我们从系统的稳定性开始，也就是检测优化方法消除牛鞭效应的能力。

我们选取一个供应链为3级，运行周期为20的例子，其他相关数据见下表：

表3-1 分析算例数据

基于以上数据，本文利用鲁棒优化，广义鲁棒优化和乌托邦优化等优化方法，并给出相应的仿真效果图，如图3-1和图3-3所示。

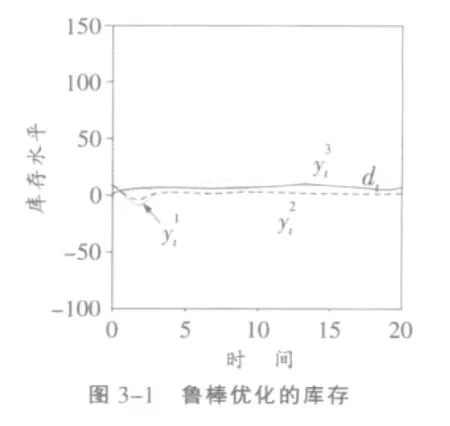
图中，实线dt代表库存的变化状况，分别代表3个不同节点的库存表现。从图中不难发现，3种优化方法优化的库存都不存在牛鞭效应，但有趣的是利用鲁棒优化时，零售商的库存波动幅度超过了制造商库存波动的幅度[12]。利用鲁棒优化，各级库存表现都很稳定，各级供应链的最高库存水平不超过30，在第三阶供应链最低库存为-20，每级供应链库存波动幅度均未超过外界需求变动的5倍。利用乌托邦优化时，在任何给定周期内，每级供应链的订货量都刚好等于其需求量，所以库存水平为0，也不存在持有成本和缺货成本。即便使用最有优化方法，在周期开始和结束阶段仍然存在 “边界特性”，应为初始阶段库存水平不为0，系统需要时间来稳定库存并最终实现0库存。

4 结束语

本文选取了一种广泛并普遍适用的供应链控制解决方案，试图在协同理论的框架下，从经济角度优化供应链库存。为达到这一目的，本文应用了广义鲁棒优化，这种方法可以较好地处理不确定性需求下的优化问题并能保证系统的稳定。本文选取了m=3，n=20的3级20周期供应链，其中大约包含了40 000个约束和25 000个变量，比较了广义鲁棒优化和鲁棒优化的方程，并选用了乌托邦优化这种并不实际的优化方法，试图找出在需求已知的情况下的最优库存。并把乌托邦优化值作为参考值，研究表明了鲁棒优化可以减弱牛鞭效应，并能得到近似于乌托邦值的优化结果。

[1] Blanchini,F.,Miani,S.,&Rinaldi,F..Guaranteed cost control for multi-inventory systems with uncertain demand[J].Automatica,2004(2):213-223.

[2] Braun,M.W.,Rivera,D.E.,Flores,M.E.,Carlyle,W.M.,&Ke.A model predictive control framework for robust managementof multi-product,multi-echolon demand networks[J].Annual Reviews in Control,2003(27):229-245.

[3] Robbins,H.,&Monro,S..A stochastic approximation method[J].Annals of Mathematical Statistics,2007(3):400-407.

[4] Blanchini,F.,Miani,S.,&Rinaldi,F..Guaranteed cost control for multi-inventory systems with uncertain demand[J].Automatica,2004,40(2):213-223.

[5] Kempf,K.G..Control-oriented approaches to supply chain management in semiconductor manufacturing[Z].In Proceedings of the 2004 American Control Conference,2004:4563-4576.

[6] De Brentani U.Innovative versus incremental new business services:different keys for achieving success[J].Journal of Product Innovation Management,2008,18(3):169-187.

[7] Harambos Sarimveis,Panagiotis Patrinos,Chris D.Tarantilis,Chris T.Kiranoudis.Dynamic Modeling and control of supply chain system:A reviem[J].Computers and Oprations Research,2000,24:1143-1149.

[8] Osear Rubiano Ovallea,Adolfo Crespo Marquez.The effectiveness of usingcollaboration Tools In the Supply chain:an assessment study with system dynamic[J].Journal of Purchasing&Supply Management,2003(9):151-163.

[9] Selwyn Piramuthu.Knowledge-based frame work for automated danamic supply chain Configuration[J].European Journal of Operational Research,2005(16):219-230.

[10] Martha.C.Wilson.The impact of transportation disruptions on supply chain performance[J].Transportation Research Part E,2007,43(2):295-320.

[11] Yossi A.Federgruen A.The operational benefits of information sharing and Vendor Managed Inventory programs[R].Olin School of Business,Washington University,1998.

[12] 谢五洲，郭成恒.物流企业库存周转率指标的分析与评价[J].现代物流，2007(5):66-67.

Research on the Multi-Echelon Multi-Period Optimization Model for Inventory Management Based on robust Optimization

LIU Bao-xing, LIU Liang, HAN Ji-fang, XU Bo (The Material Supply Station of China Aviation Technology Research Institute,Beijing 100074,China)

在考虑了供应链库存综合成本构成及假设的基础上，构建了基于鲁棒优化的多级多周期库存管理优化模型，在对模型优化的同时，利用算例分析和仿真分析呈现优化效果。

库存优化；鲁棒优化；仿真分析

This paper considers the integrated supply chain inventory cost structure and assumptions built based on robust optimization-based multi-level multi-period optimization model for inventory management,while in the model optimization,the use of analysis and simulation examples show the optimization effect.

inventory optimization;robust optimization;simulation

F224.0

A

2011-01-18

刘宝兴（1959-），男（满族），辽宁黑山人，中国飞航技术研究院物资供应站，研究员，硕士，研究方向：机械制造及其自动化；刘 亮（1966-），男，辽宁沈阳人，中国飞航技术研究院物资供应站，工程师，研究方向：市场营销；韩继方（1980-），男，贵州遵义人，中国飞航技术研究院物资供应站，工程师，研究方向：工商管理；许 波（1983-），男，黑龙江克山人，中国飞航技术研究院物资供应站，工程师，硕士，研究方向：物流与供应链管理。

1002-3100(2011)03-0016-04