基于相对熵原理的大型工程项目交互式多属性群决策方法研究

雷丽彩 ，周 晶 ，李 民

(南京大学工程管理学院，江苏南京 210093)

基于相对熵原理的大型工程项目交互式多属性群决策方法研究

雷丽彩 ，周 晶 ，李 民

(南京大学工程管理学院，江苏南京 210093)

由于大型工程决策涉及多元决策主体和多层次决策目标，不可避免会引起冲突。如何有效集结决策群体的偏好以协调决策者之间的冲突，是研究的主要目的。本文基于不确定多属性群决策理论的研究视角，分别利用交互式的线性规划模型和优化原理求解属性权重和专家权重，然后基于相对熵原理集结决策群体的不同偏好信息，最后用一个工程实例来验证该方法

多属性群体决策;相对熵;工程决策;大型建设工程

tion project;

一、引言

在工程活动中，决策活动贯穿于工程建设全过程［1］，文献［2］在研究综合集成管理职能时指出复杂决策是综合集成管理的重要职能，正确、科学和民主决策是大型工程各项工作成功的重要前提。由于大型工程的规模庞大、涉及的因素众多且相互关系复杂、后果影响重大［3］，大型工程决策问题是一类复杂的非结构化决策问题;尤其大型工程决策是一项涉及到多元利益相关者(Stakeholders)、多层次决策目标的复杂系统工程，工程建设过程中会面临各种来自工程本身和环境的错综复杂的不确定因素，其决策需要跨行业和多部门的专家进行群体共同决策，而各个专家由于心理、行为、文化、气质等之间的差异，对于同一问题的认识、思考、价值判断与评价不同，在决策过程中可能会存在一种对抗的心理;并且大型工程项目决策所需要的信息量极大，而有限理性的决策者［4］很难也不可能掌握决策所需要的全部信息，由此对同一问题可能出现完全不同的看法，从而不可避免地会产生矛盾，引起冲突，使得工程项目决策管理的复杂性急剧增加［5］。因此，如何在大型工程的不同利益主体间寻找一致或妥协的满意方案以协调大型工程决策者之间的冲突关系，建立大型工程的协商决策机制，使决策者由初始的“对抗”心理逐渐转变为“对话”心理，从而为正确科学的工程决策提供依据，是工程项目管理领域在理论和实践上发展的迫切需要。

全球迅速增长的大型工程项目，以及计算机科学与信息技术、运筹学等学科的迅速发展，都促进了国内外有关大型工程决策理论和实践两个方面的探讨和现代项目决策机制的建立与完善。例如，Hector等(2009)从哲学、心理和系统这三个维度分别探讨了大型基础设施可持续发展的决策问题并提出一种新的解决方法［6］。Lam(2009)等以中国的大型国有建筑公司为研究对象，基于遗传算法(Gene Algorithm)研究在模糊条件下建筑公司的多目标财务决策支持模型［7］。而Cheng和Roy提出由于大型工程复杂和多变的特质，其成功的决策在很大程度上依赖于决策者在实践中累积的经验和知识，他们利用支持向量机(Support Vector Machine)构建了大型工程的进化模糊决策模型［8］。同时，我国的学者卢广彦等(2008，2009)研究了重大工程决策的信息强依赖性、时机非敏感性、多元决策思维向度集成以及决策过程动态演化等特征，分析总结了国内外重大工程决策失误的经验教训，提出了构建我国国家重大工程决策机制的相关建议［9］，［10］。谢洪涛和王孟钧通过问卷调查，考察我国重大工程项目决策阶段工作的现状，分析存在的问题，并在此基础上探讨改善决策工作质量的方式和途径［11］。这些研究从不同的视角，利用不同的方法和思路，并结合各类大型工程项目的特点，将不同的决策理论与方法运用到项目决策中，为大型工程项目制定合理的决策提供理论指导和借鉴。虽然目前关于大型工程项目决策的研究成果比较丰富，但总的来说其还没有形成一个完整的体系，许多研究只是在单个问题及个别分析模型和方法上进行探讨，还存在一些问题需要进一步深入讨论与探索，主要体现在：现有的大型工程项目决策研究没有考虑决策主体的有限理性行为和决策问题的复杂性;没有建立引导决策主体进行科学决策的机制;更缺乏关于如何有效协调不同决策主体间的冲突关系的协商决策机制的系统研究。

虽然群决策研究日益受到国内外学者的广泛关注［12］，且已经涉及了众多领域，但在研究方法上总体而言，主要集中在群体的信息偏好集结上，主要包括：概率偏好集结、基于语言形式的信息集结［13］、模糊偏好关系集结［14］和多种偏好信息形式集结［15］。针对不同情境下的决策问题提出了丰富的决策分析模型和方法，如TOPSIS(Technique for Oder Preference by Similarity to Ideal Solution)法［16］、有序加权平均(Order Weighted Average，OWA)算子［17］、证据推理理论(Evidence Reasoning Theory)［18］等。在各种决策理论与方法中，利用相对熵方法能够衡量群决策中决策者偏好一致的程度，从而将不同专家的偏好评判值集结为群体一致的或妥协的偏好，有效协调不同决策者之间存在的利益或意见冲突关系，使群决策的一致性实现极大化，亦即极小化最终的群决策结果与个人偏好的不一致的可能性。但是在目前的研究中一般都假设专家权重和属性的权重相同或事先赋值，然而由于大型工程决策问题具有很强的模糊性和不确定性，且工程项目中不同专家的专业知识、认知能力以及实践经验都各不相同，简单假定属性权重和专家权重为已知参数，将对工程最终的决策结果带来很大的不利影响。现有文献对属性权重［19］和专家权重［20］的确定问题研究得较少。

目前，熵的应用已经涉及几乎所有学科领域，被爱因斯坦誉为“整个科学的首要法则”。许多学者已经将熵的概念和熵的优化原理成功运用于决策分析上［21］，［22］，并取得了许多很好的研究成果［23］。和信息熵类似，相对熵(Relative Entropy)也可以用于度量系统的不确定性和无序性。邱菀华等学者首先基于相对熵的概念得到一个新的群决策集结模型——相对熵集结模型(Relative Entropy Model，REM)并证明相对熵集结模型得到的集结公式与Bordely利用公理得出的集结公式在形式上非常相似［24］，［25］。因此，一些学者将相对熵应用于其他优化问题中，如Sandroni基于相对熵的思想研究了资产定价的决策模型［26］，Bao利用相对熵最小化方法预测生产系统中的生产提前期的随机分布［27］，而Xue利用相对熵理论集结工程供应链中各参与方的偏好信息，并提出改善谈判效率的有效方法［28］。另外，文献［29］针对传统的REM模型在确定专家权重方面的不足而提出一种基于熵可靠性的赋权方法。

本文在文献［28］的基础上，考虑大型工程决策问题的模糊性和不确定性特征，分别利用交互式的多属性群决策(Multi-Attribute Group Decision Making，MAGDM)协商模型和优化原理来求解大型工程决策的属性权重和专家权重，在不同利益主体间寻找一致或妥协的满意方案，使其赋权更加客观合理，从而客观反映每个属性的相对重要性以及专家的决策水平。然后利用相对熵理论将不同决策者的偏好信息集结为群体一致或妥协的偏好，有效协调不同决策者之间可能存在的利益或意见冲突关系，建立大型工程的协商决策机制。其基本思想在于利用相对熵方法来集结决策群体的不同偏好信息，极大化群决策的一致性，亦即极小化最终的群决策结果与个人偏好的不一致的可能性。最后以某跨界大桥工程中的隧道人工岛位置选择的决策实例来验证该方法，研究结果对于大型工程建设项目的复杂多属性群决策问题具有一定的理论价值和现实意义。

二、基于相对熵的大型工程交互式多属性群决策模型

(一)问题说明和符号说明

由于工程系统的开放性，现实中的大型工程决策通常涉及的因素众多，其间的关系错综复杂，工程决策者需要组织进行大量的试验和关键技术攻关，然而并非所有的工程问题都能通过试验和攻关一次性彻底解决，即最优方案有时需要花费过高的代价或太长的时间才能获得，而工程的建设又不能因此而停工不前，这时就需要决策者在现有能力和有限理性的约束下终止漫长的“寻优”过程，从而制定较为可行的“满意”方案，并且不断地深入认识和完善方案。所以大型工程复杂性决策普遍存在的一个问题是决策方案的制定不能“一蹴而就”，也不能“一劳永逸”，需要决策主体进行多次讨论、协商、比对和调整后进而获得决策群体都能接受的“妥协解”(Compromise Solution)或满意解，使工程决策的可行域随着信息的完备逐步收敛到最优方案。

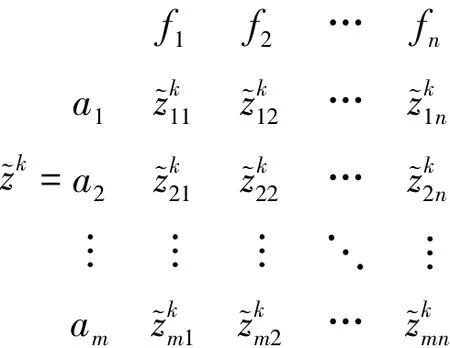
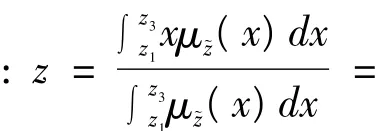
另外，由于在多属性决策问题中有两种类型的属性：效益型属性(benefit attribute)和成本型属性(cost attribute)［31］，为了便于属性之间的比较分析，我们对决策矩阵中效用值进行标准化处理，即：对于效益型属性，令

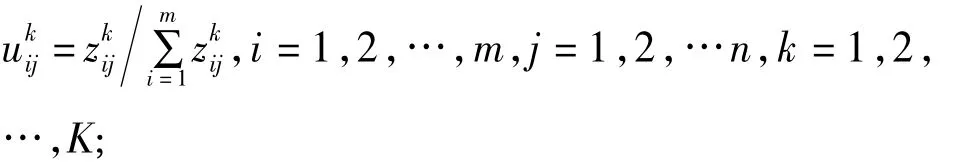
对于成本型属性，有

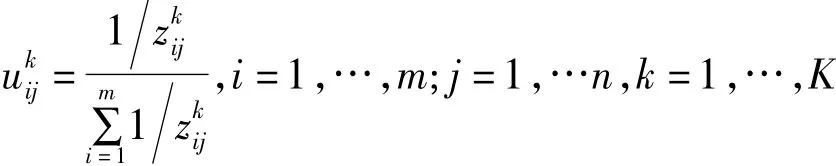
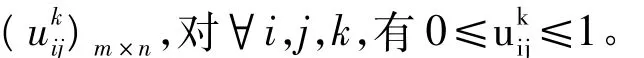
在给出大型工程多属性群决策协商模型的交互式求解算法之前，根据文献［32］和［33］我们先给出下面两个定义：

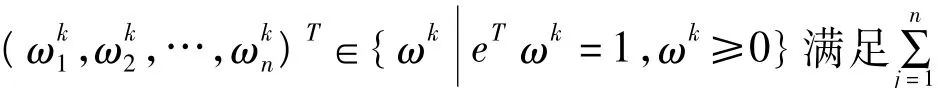
其中 1≤r，s≤m，r≠s，e=(1，1，…，1)T∈Rn，而β则反映了方案ar优于方案as的程度，ωk为决策者ek所认为的属性权重向量。

定义2中各符号的含义说明如下：不是一般小，假设决策者ek对所有方案分别进行两两成对比较，由此得到的偏好顺序为ak(1)＞ak'(1)，ak(2)＞为决策者 ek的偏好关系中方案两两成对的数量(例如决策者e1的偏好顺序为 a3＞a1，a3＞a5，则 I1={(3，1)，(3，5)};决策者 e2的偏好顺序为 a2＞a1，a2＞a4，a5＞a3，则 I2=。而，其中(r，s)∈UKk=1Ik。

综上所述，给出大型工程的多属性群决策问题的交互式求解过程如下，决策流程图如图1所示。

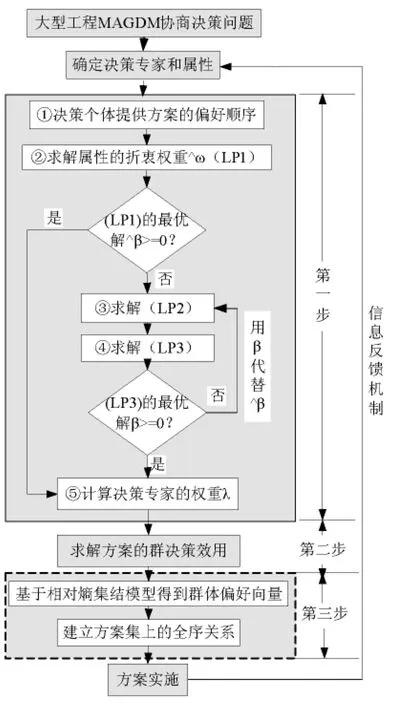
图1 大型工程的多属性群决策问题的交互式求解流程图

(二)求解大型工程多属性群决策的属性妥协权重和决策者权重

类似文献［34］和［28］，大型工程项目的多属性群决策的属性妥协权重求解过程如下：

(1)各个决策者给出他们对方案进行两两成对比较的偏好顺序，由此得到Ik和urs。(2)将决策者对各个方案的效用函数作为大型工程决策问题的目标函数，不失一般性，我们假设每个属性的边际效用函数独立(Functionally Independent)。根据期望效用理论，应用线性加权法可得方案ai的多属性效用(Multi-Attribute Utility，MAU)函数 V(ai)为：

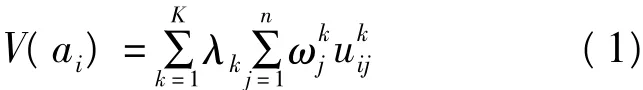
在上述效用函数中，由于属性的权重向量ωk和决策专家的权重λk均未知，无法利用上述效用函数建立方案集上的全序关系，因此本文首先用线性规划(Linear Programming，LP)来寻找属性权重向量的值，其线性规划模型(LP1)如下：

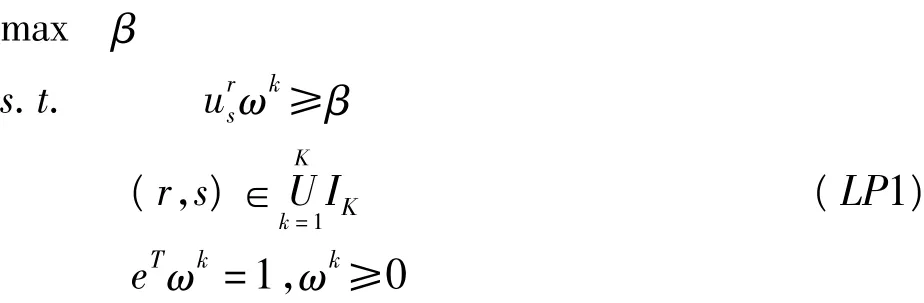
令上述线性规划模型(LP1)的最优解为β^和ω^k，则下述结论成立：如果 β^≥0，则k个决策者没有任何异议地一致认同方案ar＞as，(r，s)∈kUK=1IK，其中ω^k为所有决策者都满意的属性的妥协权重;若β^＜0，说明妥协权重不存在，即决策者之间达成一致认同的意见，这时需要决策者们调整部分偏好以达到一致意见，则转(3)。

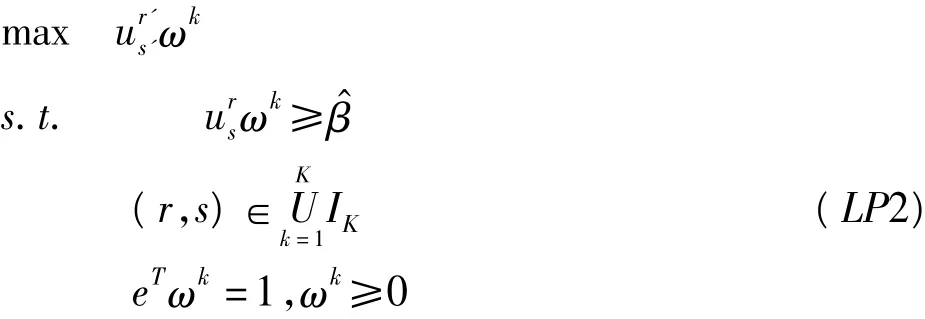
(4)根据上述的求解过程，构建下面的线性规划模型(LP3)

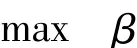
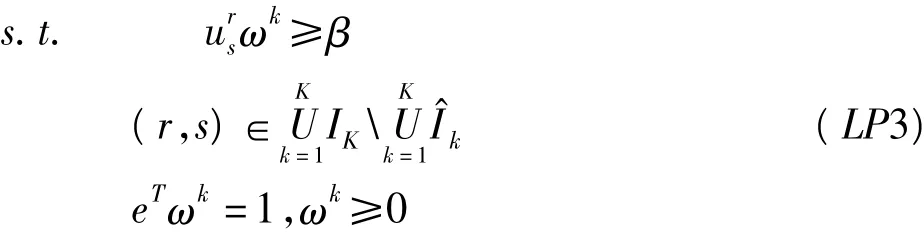
令线性规划模型(LP3)的最优解分别为¯β和¯ωk，如果 ¯β≥0，，则 ¯ωk为所有决策者均接受的属性的妥协权重;而如果 ¯β ＜0，则用 ¯β代替步骤(3)中的 β^，转(3)。

(5)由上述的集结过程，已经求得属性的折衷权重，将之代入效用函数公式(1)即可求得决策者e关于方案a的效用值但由于决策ki专家的权重向量未知，从而仍然无法确定方案集上的全序关系。各决策专家一般具有不同的知识背景、认知水平和实践经验，故专家权重的确定应充分反映出专家的决策水平，不能同等看待。下面给出一种基于模糊集理论的赋权方法，可以客观地反映专家的决策水平。这一指标的计算过程实际上可以看成是文献［35］的一种特殊形式，具体计算过程如下：将决策者ek关于方案ai的效用值Vki转化成三角模糊数：

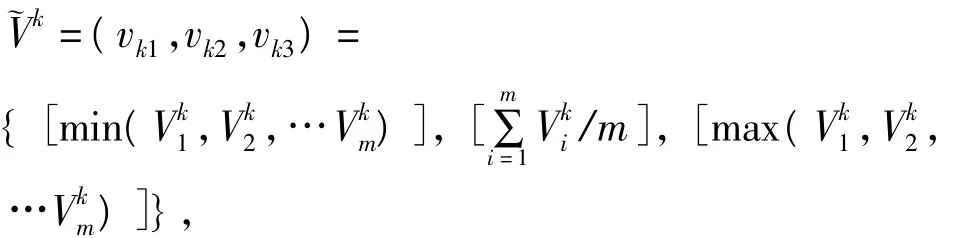
式中vk1为决策者ek最不喜欢的方案的效用值，代表悲观估计值;而vk3表示决策者ek最偏好的方案的效用值，代表乐观估计值;而vk2表示决策者ek认为最有可能被采纳的方案的效用值。文献［35］已经证明决策者专家的权重ek的最优值为

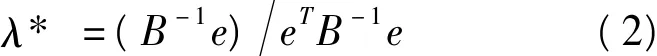
其中矩阵B为：

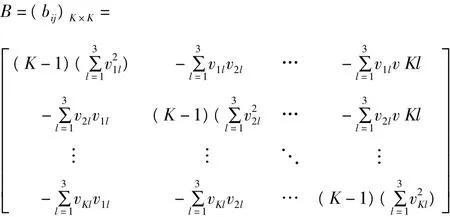
由此可以客观求出每个决策专家的权重，从而避免了主观赋权的诸多不利之处。

(三)基于相对熵的大型工程多目标协商决策模型的群体偏好集结

大型工程多属性群决策的属性的妥协权重和决策者的权重已知后，就能将其带入效用函数公式(1)计算每个方案的效用值，但是如何集结决策群体的偏好信息使决策群体的偏好的一致性最大化，协调不同决策者之间的利益或意见冲突关系，从而建立方案集上的全序关系?为此，下面利用相对熵集结模型［23］来集结决策群体的偏好，首先根据shannon的信息熵理论［36］，给出相对熵离散形式的概念和性质如下：

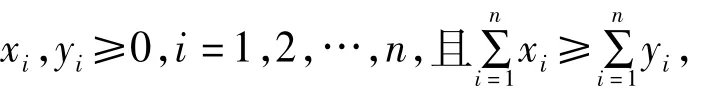
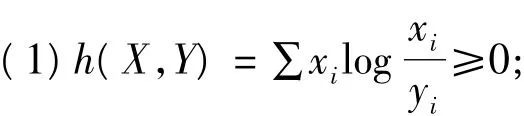
根据上述性质，当X、Y为两个离散分布时，相对熵可用于度量二者符合程度，且X和Y的分布相同时，其相对熵值最小［32］。因此，我们可以用相对熵来定量衡量大型工程多属性群决策中决策者偏好一致的程度［37］：相对熵值为0表示群体意见达到完全共识，没有任何分歧意见;相对熵值为1则意味着决策群体没有达成一致的共识，每个决策个体都各持己见，意见分歧较大。

∀k，如果将决策者ek对决策方案集合A={a1，a2，…am}中的各个方案的效用值作为对各个方案偏好效用的概率测度，每个决策者对方案集合中所有方案的离散概率测度形成决策方案集合A={a1}，i=1，2，…m的一个概率分布。不失一般性，我们假设决策者是在相互独立的情况下评判各个方案的属性值，即决策方案的概率分布是相互独立的。

令 Vg={Vgi}，i=1，2，…，m 为决策群体关于各个方案的偏好向量，其中Vgi表示方案ai的群效用值。根据相对熵的性质，为了最大化决策群体偏好的一致性，就要使群效用值相对于每个决策者个体的效用值的相对熵最小，即要求下述优化问题：

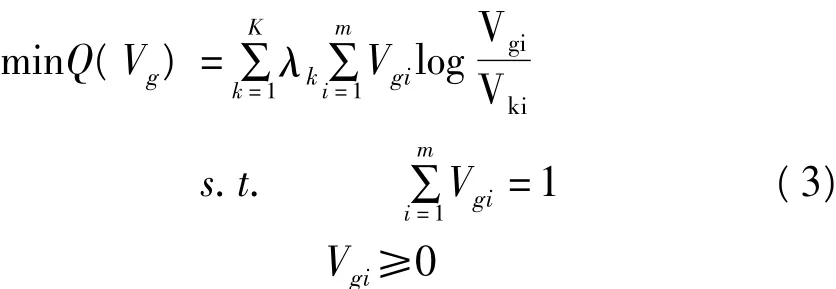
其中Vki表示决策者ek关于方案ai的效用值。

文献［23］已经证明上述优化问题(3)的最优解为V*g={V*gi}，i=1，2，…，m，其中

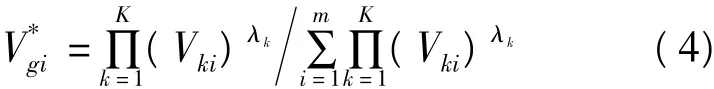
则根据V*gi的值能得到所有决策者均接受认可的“满意”方案。

三、算例分析

以我国目前正在施工的某跨界大桥工程的“隧道东人工岛位置选择”为例来验证本文提出的方法。该跨界大桥工程涉及三个地方政府(三地政府组成了该工程的决策群体e1、e2、e3)，他们对于大桥建设工作有着各自的偏好和利益选择，这些利益偏好在某些方面可能会存在相互冲突，需要在三地政府间寻找一致或妥协的满意方案。隧道东人工岛位置比选中主要遵循以下原则［38］：①隧道口门宽度满足航道通航及安全宽度要求并利于减小船舶撞击风险;②隧道长度在合理的范围内，满足工程技术可行性，降低隧道建设运营期间风险，保证隧道内车辆行驶安全;③隧道人工岛布置应尽量减少对附近水域水动力的影响，减小对环境的影响，减小对入海口滩槽冲淤变化的影响;④方便建设运营管理，降低建设及运营成本。因此本文总结为下述5个属性：隧道建设运营成本(f1)、船舶航运风险(f2)、建设运营风险(f3)、对水域水动力及23DY锚地等环境的影响(f4)、建设运营管理复杂性(f5)。

考虑西人工岛位于推荐的位置，结合《某某大桥隧道极限通风长度专题研究》的研究结论，针对不同的隧道东人工岛位置提出五种总体布置方案：a1、a2、a3、a4和 a5。各方案在上述五个属性下的情况详见表1。

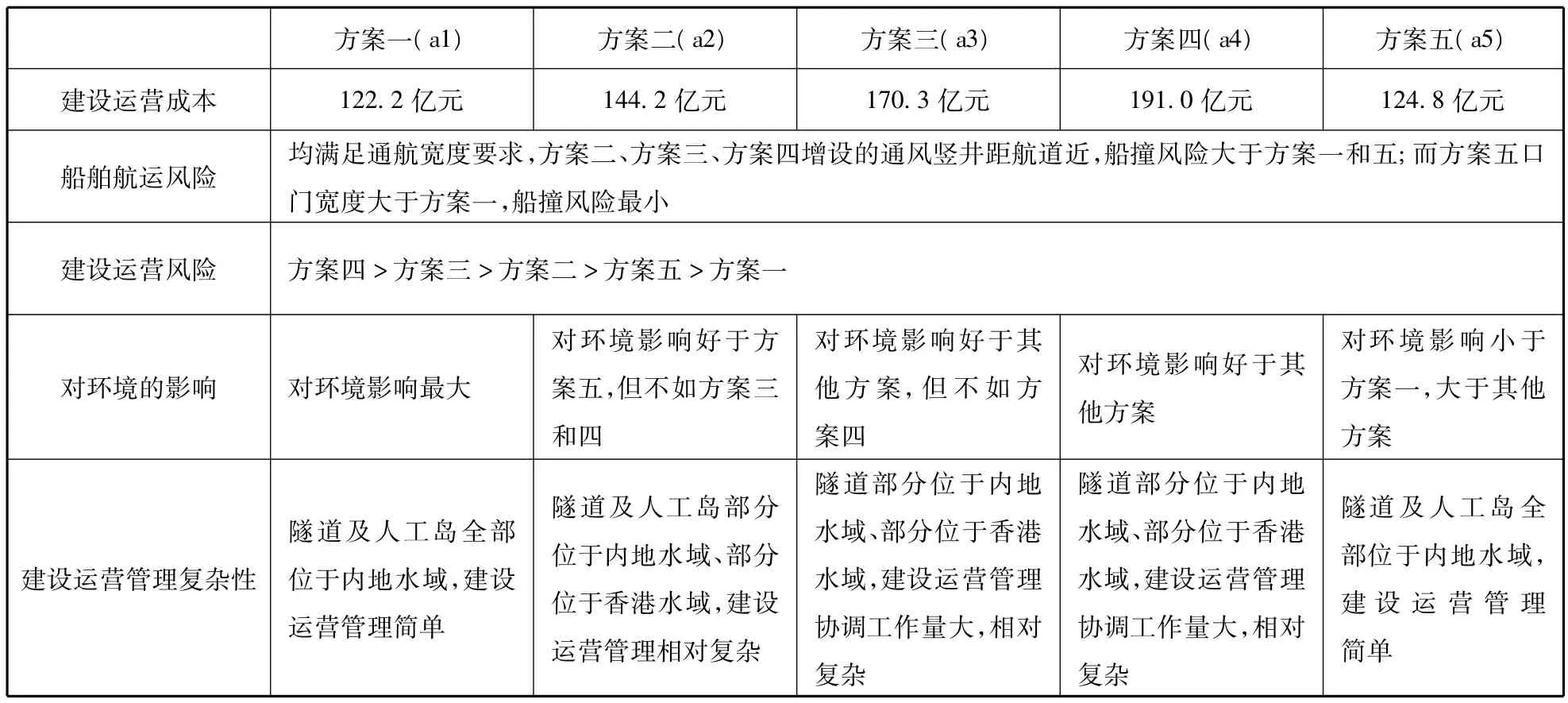
表1 某跨界大桥工程不同隧道东人工岛位置方案综合比选［38］

由表1可知，各个备选方案在不同的属性准则下表现出不同的优先顺序，决策者无法根据自己的直觉来判断各个方案的优劣。因此，我们试图采用本文的优化方法建立方案集上的优先顺序，并将我们得到的结论与该跨界大桥工程实际的决策结果进行对比，以验证该方法的可行性。根据《某某大桥工程可行性研究报告》中提供的相关定性分析和三地政府的工作意见［38］，假设决策者 e1对于该工程的模糊决策矩阵 ˜Z=(˜zij)m×n为：

由于五个属性均为成本型属性，将模糊决策矩阵转化成期望决策矩阵并进行规范化处理得到决策者e1的标准决策矩阵如下：

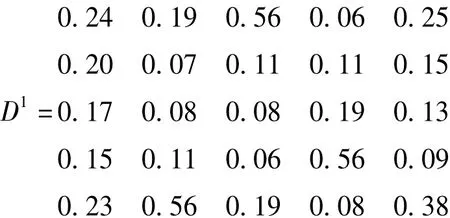
同理，可得决策者e2和e3的标准化决策矩阵如下：

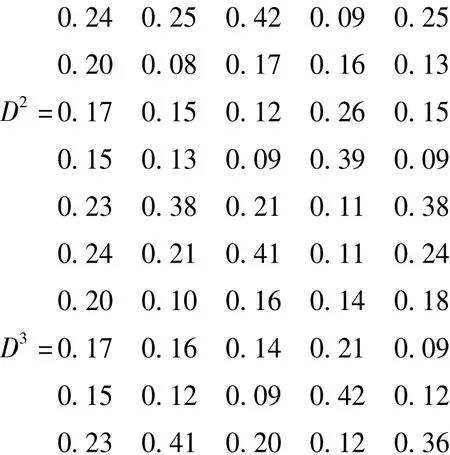
(1)在大型工程协商决策过程中，假设所有的决策者都是理性的经济人。在隧道东人工岛位置比选决策中，三地政府对于这五个方案既存在基本的利益一致，也都有着各自的偏好和利益选择，为使三地政府对决策方案形成较为一致的共识，不能仅仅对各决策主体的目标、规则和行为进行简单的叠加和归纳，而是要对不同利益主体的目标的偏好进行系统的分析。三地政府对这五个方案的偏好顺序如下：

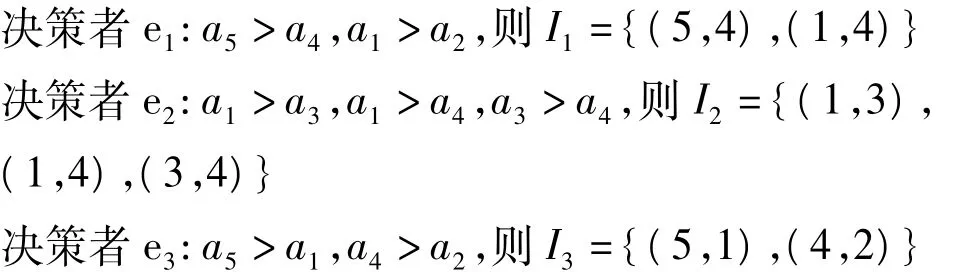
由此可得：

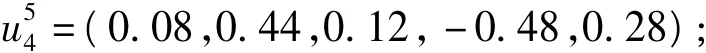
(2)用线性规划模型求解属性权重向量的值，得到各个决策者所认为的属性权重向量值为：

由此可得：

根据式子(2)求得决策者的权重向量为λ=(0.3422，0.3327，0.3251)T。

相对熵可以用来定量衡量多属性群决策中偏好一致性的程度。根据相对熵的性质，为了最大化决策群体偏好的一致性，就要使群效用值相对于每个决策者个体的效用值的相对熵最小，因此，利用相对熵集结模型的公式(4)来集结三地政府对五个备选方案的偏好顺序，使最终的决策结果能够实现群体偏好的一致性最大化。由此得到该工程项目隧道东人工岛位置方案比选的决策群体的偏好向量 为 Vg=(0.2432，0.0928，0.1356，0.1491，0.3793)，因此方案集上最终的全序关系为 a5＞a1＞a4＞a3＞a2，则最终的满意方案为 a5，即隧道东人工岛东边最近点距离粤港分界150m为最终的满意方案，与该跨界大桥工程项目实际推荐的最终方案［38］相吻合。运用本文方法得到的结果与工程实际的推荐方案一致，在一个方面佐证了本文的方法在一定程度上是可行的，在另一方面，本文提出的方法相对其他其他方法而言操作相对简便，计算量也不大，是一种简便易行的方法，也体现了该方法是可行的。

四、小结

首先，决策专家的权重代表了专家在大型工程决策过程中的决策权力，各专家由于具有不同的知识背景、实践经验和认知水平，偏好也不尽相同，故专家权重的确定应充分反映专家的重要性和决策水平。属性的权重也同样反映了不同属性在形成决策时的重要程度。迄今为止，大部分的群决策方法都假设属性的权重和决策者的权重相等或事先已经赋值，这就带有较大的主观性。而现实中的大型工程决策环境往往是复杂多变的，并且由于时间压力、缺乏数据或经验等，决策者往往不能精确确定属性的权重和专家权重，因此本文采用交互式的多属性群决策协商模型和优化原理来求解属性的权重和决策者的权重，在不同利益主体间寻找一致或妥协的满意方案，使其赋权更加客观合理，避免主观赋权的不足之处。

另外一方面，在复杂性决策过程中，决策主体之间既存在基本的利益一致，也存在着利益和偏好冲突。相应的，决策管理的重要任务之一就是要协调主体间的冲突关系，使各决策主体对决策问题形成较为一致的共识。实践证明，处理决策主体自主博弈的问题不能只对各主体的目标、规则和行为进行简单的叠加和归纳，而要对不同利益主体的目标进行系统的分析，对运作的机制进行设计与优化，从而更好地引导各决策主体趋于一致。而相对熵可以定量度量群体偏好一致性的程度。因此，本文利用相对熵理论将不同决策者的偏好信息集结为群体一致或妥协的偏好，使最终的群偏好与个人偏好的不一致的可能性最小化，有效协调不同决策者之间可能存在的利益或意见冲突关系，建立大型工程的协商决策机制，具有一定的理论价值和现实意义。

本文的研究虽然考虑大型工程决策的模糊和不确定性特征，但是假设在大型工程协商决策过程中，所有的决策者都是完全理性的经济人，而现实的工程决策者往往是有限理性的，因此，有限理性决策者假设条件下的大型工程决策机制仍需进一步的验证和研究。

［1］游庆仲，何平，盛昭瀚等.苏通大桥工程建设管理实践与基本经验［M］.北京：科学出版社，2009

［2］程书萍，王茜，李迁.关于综合集成管理职能的探索［J］.科学决策，2009，(1)：1-5

［3］席酉民.大型工程决策［M］.贵阳：贵州人民出版社，1988

［4］［美］赫伯特A.西蒙.管理行为［M］.北京：机械工业出版社，2008.

［5］盛昭瀚，游庆仲，程书萍，姚蓓.苏通大桥工程系统分析与管理体系［M］.北京：科学出版社，2009

［6］Hector D.，Christensen C.，Petrie Jim.A Problem-Structuring Method for Complex Societal Decisions：Its Philosophical and Psychological Dimensions［J］.European Journal of Operational Research，2009，193：693-708

［7］Lam K.C.，Ning X.，Gao H.The fuzzy GA-based Multi-objective Financial Decision Support Model for Chinese State-owned Construction Firms［J］.Automation in Construction，2009，18：402-414

［8］Cheng M.Y.，Roy A.F.V.Evolutionary Fuzzy Decision Model for Construction Management Using Support Vector Machine ［J］.Expert Systems with Applications，2010.Doi：10.1016/j.eswa.2010.02.120

［9］卢广彦，付超，吴金园，刘源.重大工程决策过程与决策特征研究——以三峡工程为例［J］.中国科技论坛，2008，(8)：20-24

［10］卢广彦.重大工程决策失误与重大工程决策机制构建［J］.中国科技论坛，2009，(4)：30-35

［11］谢洪涛，王孟钧.我国重大工程项目决策阶段工作现状与问题问卷调查分析［J］.中国工程科学，2010，12(1)：18-23

［12］Xu Z.S.，Chen J.Some Models for Deriving the Priority Weights from Interval Fuzzy Preference Relations［J］.European Journal of Operational Research，2008，(184)：266-280［13］Dong Y.C.，Xu Y.F.，Li H.Y.On Consistency Measures of Linguistic Preference Relations［J］.European Journal of Operational Research，2008，(189)：430-444

［14］Wang T.C.，Chen Y.H..Applying Consistent Fuzzy Preference Relations to Partnership Selection［J］.Omega，2007，(35)：384-388

［15］Fan Z.P.，Ma J.，Jiang Y.P.，Sun Y.H.，Ma L.A Goal Programming Approach to Group Decision Making Based on Multiplicative Preference Relations and Fuzzy Preference Relations［J］.European Journal of Operational Research，2006，(174)：311-321

［16］Lin Y.H.，Lee P.C.，Chang T.P.，Ting H.I.Multiattribute Group Decision Making Model Under the Condition of Uncertain Information［J］.Automation in Construction，2008，(17)：792-797

［17］Chiclana F.，Herrera-Viedma E.，Herrera，F.Alonso S.Some Induced Ordered Weighted Averaging Operators and Their Use for Solving Group decision-making Problems Based on Fuzzy Preference Relations［J］.European Journal of Operational Research，2007，(182)：383-399

［18］Guo M.，Yang J.B.，Chin K.S.，Wang H.W.Evidential Reasoning Based Preference Programming for Multiple Attribute Decision Analysis under Uncertainty.European Journal of Operational Research，2007，182：1294-1312

［19］周宇峰，魏法杰.基于相对熵的多属性决策的组合赋权方法［J］.运筹与管理，2006，15(5)：48-53

［20］叶帆，洪振杰.不完全信息群体决策专家权重的集结［J］.应用数学与计算数学学报，2006，20(1)：63-67

［21］Lehrer E.，Smorodinsky R..Relative Entropy in Sequential Decision Problems［J］.Journal of Mathematical Economics，2000，33：425-439

［22］Olcer A I，Odabasi A Y.A New Fuzzy Multiple Attribute Group Decision Making Methodology and its Application to Propulsion Manoeuvring System Selection Problem［J］.European Journal of Operational Research，2005，166(5)：93-114

［23］邱菀华.管理决策与应用熵学［M］.北京：机械工业出版社，2002：290-302

［24］魏存平，邱菀华，杨继平.群决策问题的REM集结模型［J］.系统工程理论与实践，1999，19(8)：38-41

［25］万树平.基于相对熵的不完全信息群体专家权重的集结［J］.应用数学与计算数学学报，2009，23(1)：66-70

［26］Sandroni A.Do Markets Favor Agents able to Make Accurate Predictions? ［J］.Econometrica，2000，68(6)：1303-1341

［27］Bao X，Tang O.，Ji J.H.Applying the Minimum Relative Entropy Method for Bimodal Distribution in a Remanufacturing system［J］.International Journal of Production Economics，2008，113：969-979

［28］Xue X.L.，Shen Q.P.，L H.，O’Brien W.J.，Ren Z.M.Improving Agent-based Negotiation Efficiency in Construction supply Chains：A Relative Entropy method［J］.Automation in Construction，2009，18：975-982

［29］邱菀华，刘北上，侯琳琳.基于熵可靠性的相对熵集结模型［J］.系统工程，2008，26(5)：80-84

［30］Bortolan G.，Degani R.A Review of Some Methods for Ranking Fuzzy Subsets［J］.Fuzzy Sets and Systems，1985，15：1-19

［31］Xu Z.S.，Chen J.An Interactive Method for Fuzzy Multiple Attribute Group Decision making［J］.Information Sciences，2007，177：248-26

［32］Wei Q.L.，Yan H.，Ma J.，Fan Z.A Compromise Weight for Multi-criteria Group Making with Individual Preference［J］.Journal of Operational Research Society，2000，51：625-634

［33］Yan H.，Wei Q.L.Determining Compromise Weights for Group Decision-making［J］.Journal of Operational Research Society，2002，53：680-687

［34］魏权龄，闫洪.广义最优化理论和模型［M］.北京：科学出版社，2003，310-320

［35］Yu L.，Wang S.Y.，Lai K.K.An Intelligent-agent-Based Fuzzy Group Decision Making Model for Financial Multicriteria Decision Support：The case of credit scoring［J］.European Journal of Operational Research，2009，195：942-959

［36］Shannon C.，Weaver W.The Mathematical Theory of Communication， University of Illinois Press， Urbana，IL，1949

［37］Davis W.L.Economists’Opinions of Economists’Work［J］.American Journal of Economics and Sociology，2007，66：267-288

［38］中交公路规划设计院有限公司.港珠澳大桥工程可行性研究报告［R］，2009

(本文责编：海 洋)

Study on Interactive Multi-Attribute Group Decision Making Method for Large-Scale Projects Based on Relative Entropy

LEI Li-cai，ZHOU Jing，LI Min
(School of Management and Engineering，Nanjing University，Nanjing 210093，China)

Since decision making of large-scale construction project involves a wide range of decision makers and multi-level objectives，it may inevitably cause conflict.Therefore，how to aggregate group’s preference effectively to coordinate conflict among participants is the major purpose of this paper.Firstly，a new method to determine attribute weights and experts＇weights is proposed making use of interactive linear programming and optimization theory based on the uncertain multiple attribute theory.Secondly，we apply the theory of relative entropy to aggregate participants＇preference about alternatives into a single consensus or compromise one.Finally，a numerical example of project alternatives selection is used to demonstrate the feasibility and practicability of the presented approach.

Multi-attribute group decision making;Relative entropy;Project decision making;Large-scale construc

F061.5

A

1002-9753(2011)02-0166-12

2010-07-01

2010-12-08

国家自然科学基金重点项目(70831002，70971061);南京大学研究生科研创新基金(2010CW09)

雷丽彩(1984-)，女，湖南省桂阳县，南京大学工程管理学院博士生，研究方向为工程项目管理、项目决策与风险管理。