直接序列扩频系统多音扫频干扰性能分析

席有猷,程乃平

(装备学院,北京101416)

1 引 言

直接序列扩频(以下简称直扩)通信是利用高速率的伪码序列在发送端对基带数据进行频谱扩展,在接收端用相同的伪码序列进行解扩。由于直扩通信具有较强的抗窄带干扰及抗多径干扰能力,20世纪80年代开始,直扩通信广泛应用于电子战中的通信对抗[1]。

目前,国内外针对直扩系统的干扰方式很多,扫频式干扰和多音干扰是直扩系统常见的干扰形式。文献[2]提出了一种部分频段阶梯式线性扫频干扰方法,即采用阶梯式步进的方式完成扫频干扰,虽然减少了扫描时间,但牺牲了扫频精度。文献[3]对宽带扫频式干扰进行了仿真和FPGA实现。文献[4]分析了多音信号对直扩系统的干扰效果,证明了多音干扰效果依赖于音调位置,但并没有研究未知系统最佳干扰音调的位置。文献[5]仅分析了不同音调位置干扰超宽带系统时的误码率。上述研究只是分析了扫频干扰和多音干扰存在的缺点,并没有提出解决的方法。

本文针对多音干扰时音调位置难以确定以及扫频干扰时扫描时间较长的缺点,结合两种干扰策略的优势,提出多音扫频干扰技术,通过理论分析和仿真验证,证明其具有较好的干扰效果。

2 直扩系统的扫频干扰性能分析

扫频干扰就是利用一个相对窄带的干扰信号在某时间段上扫频,在扫频时间段的某一时刻,干扰信号的频率是固定的,受干扰的频谱仅仅是落在该频率附近窄带内的小部分频谱[6]。但由于干扰信号是扫频的,在长时间内可以干扰很宽的频率范围。扫频干扰最大的优势是不需要频率引导即可对敌方的某一频段无线电信号进行干扰。针对敌方的接收机,不管其工作于哪个频率,只要是在扫频带宽之内,都会受到不同程度的干扰。直扩通信系统通过频谱展宽后,大幅降低了信号的幅度。因此,通信信号的频率检测是十分困难的,扫频干扰通过干扰信号的扫描实现全频段干扰,免除了对信号频率的侦察和估计。

扫频干扰本质上是一个压制性部分频带干扰,其应用于直扩系统时,存在着一些缺点,一方面,针对直接扩频系统,扫频干扰需要扫描的带宽范围大,要求扫频速率要足够快,才能保证在有限的时间内覆盖整个频段。另一方面,为了不遗漏需要干扰的频率,扫频干扰的扫频速率要足够慢,即其频率步进要小。两者存在矛盾,需要根据实际的干扰情况进行综合考虑。单音扫频干扰原理如图1所示。

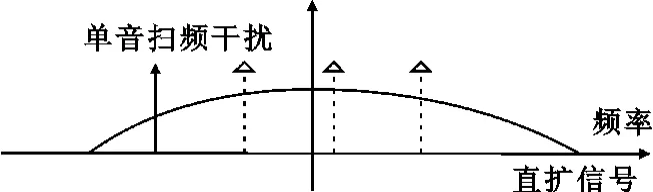
图1 单音扫频干扰原理图Fig.1 Schematic diagram of single tone frequency sweeping jamming

3 直扩系统的多音干扰性能分析

多音干扰就是根据干扰策略将多个干扰音调置于频谱内的相应的位置,这些音调的位置和数量都会影响干扰的效果,多音干扰本质是一个部分频带干扰。多音干扰原理如图2所示。

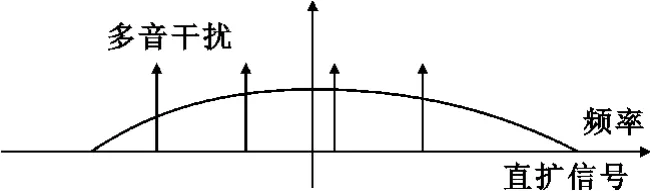
图2 多音干扰原理Fig.2 Schematic diagram of multi-tone jamming

假设在一个部分频段干扰中,干扰机功率扩展到带宽WJ上,整个信号扩频带宽为WSS,定义 γ为干扰带宽和信号带宽的比值。

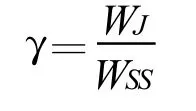
则干扰频谱密度为

其中,J0表示干扰功率扩展到整个信号带宽时的干扰能量密度。假如SJ表示干扰信号的密度函数,则对于BPSK调制的直接序列扩频信号,比特误码率为[7,8]

其中,NT是改进的噪声分量密度,为

多音信号本质也是一个部分频段干扰,可以将部分频段干扰的误码率公式推广到多音干扰直接序列扩频信号中来。设 θk表示相位差,NJ是存在的干扰音调数量,其误码率可以写为[9]

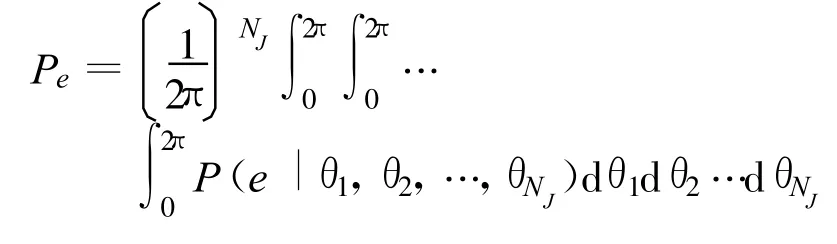
多音干扰直扩系统时,要求干扰音调在最佳干扰位置,这需要事先对直扩通信系统的载波频率等参数有正确侦察。而直扩系统优异的抗干扰能力使得侦察变得十分困难,因此,多音干扰有其使用局限性。

4 直扩系统的多音扫频干扰性能分析

针对扫频干扰和多音干扰应用于直扩系统时存在的不足,本文借鉴扫频干扰的思路,利用多音干扰的方法,提出了多音扫频干扰技术。

假设某一直扩通信系统带宽为B,将其等分为N段,则每一小段带宽为B/N,用N个多音信号从每段的起始频率开始实施扫频干扰。这样,需要完成的扫频带宽从B变为B/N,从而降低了对扫频速率的要求,同时提供了足够小的扫频频率步进。而且,多音扫频干扰是全频段扫频干扰,不需要预先考虑音调位置策略。在某一时刻,多音扫频干扰的效果相当于多音干扰,其误码率完全可以用多音干扰的误码率来表示。多音扫频干扰原理如图3所示。

式中,μ0为真空磁导率,其值为μ0=4π×10-7 N/A2,JS为面电流密度,R为曲面上一点到空间上一点的距离矢量。

图3 多音扫频干扰原理Fig.3 Schematic diagram of multi-tone frequency sweeping jamming

5 仿真验证

假设信息码的带宽为50 kHz,采样频率为40 MHz,PN码的带宽为5 MHz,则每个信息码含有800个采样点,每个PN码含有8个采样点,每个信息码内含有100个PN码,PN码采用m序列,周期为31。调制方式采用BPSK,载波信号为余弦信号,相位为0,载波频率为5 MHz,采用高斯白噪声信道,信噪比-20 dB。

假设信源信息码的长度为1 000,在Matlab仿真时,首先随机产生一位信息码,经过扩频、调制、解调、解扩、滤波和判决等直扩通信系统仿真流程,完成该信息码的通信仿真。然后,通过循环完成该信源信息序列其余码元的直扩通信仿真。单个信息码元的扩频过程如图4所示。为了显示方便,图中扩频后信号只显示整周期的1/10。仿真结果表明,在没有干扰情况下,1 000个信息码元都可以被准确还原,误码率为0。

单音扫频信号在单个信息码元传输时,其表现为一个单音干扰信号,但是在整个信息码元的传输过程中,其干扰全部系统带宽。在Matlab仿真时,单音扫频信号时域表达式可写为cos(2πf1t),扫频带宽设为10 MHz,扫描频率 f1为 0.01×i MHz,i从1递增到1 000,代表信息码元的传递过程,伴随i递增,单音扫频信号以步进0.01 MHz干扰整个频带。

图4 直接序列扩频系统仿真Fig.4 Simulation of direct sequence spread spectrum system

多音干扰信号的时域表达式为cos(2πf21t)+cos(2πf22t)+cos(2πf23t),其中,f21、f22、f23是音调频率位置,其音调出现在3个固定的频率上,因此f21、f22、f23也是固定值。

多音扫频信号首先产生有3个音调的多音信号,并将音调均匀分布在整个频带上,同时,在信息码的传输过程中,每个音调扫描调制信号的1/3带宽。其时域表达式为:cos(2πf31t)+cos(2πf32t)+cos(2πf33t),其中 t表示仿真点数 ,f31、f32、f33是多音扫频信号的频率,分别为(i-1)×0.01/3 MHz、3.34+(i-1)×0.01/3 MHz、6.67+(i-1)×0.01/3 MHz。同单音扫频信号类似,随着i的递增,多音扫频信号以步进0.01/3 MHz覆盖全部系统带宽。

先假设多音干扰信号的3个音调均匀分布在系统带宽上 ,即1 MHz、3 MHz、10MHz频率点上 ,系统的误码率仿真结果如图5所示。

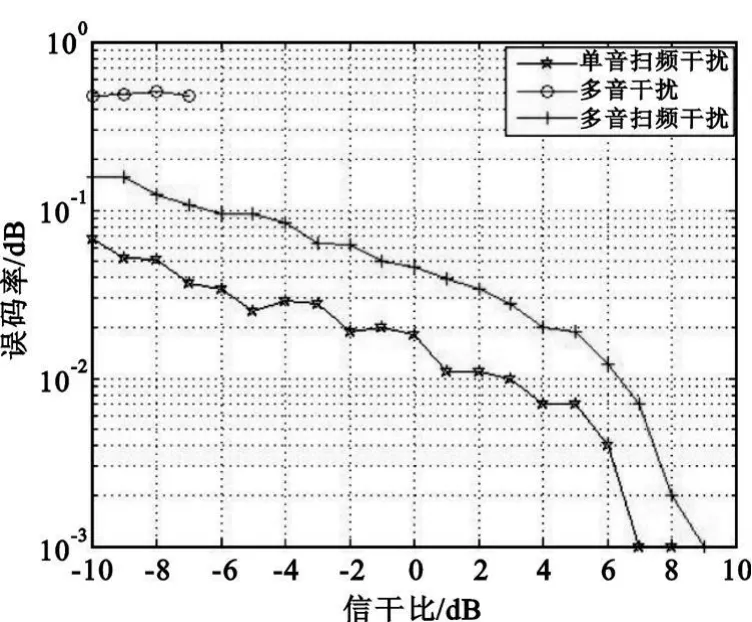
图5 不同信号干扰直扩系统误码率仿真Fig.5 Simulation of BER with Different jamming signal for DSSS system

从图5的仿真结果可以看出,3种干扰信号都可以对直扩系统产生不同程度的干扰。然而,不针对载波频率等参数专门设置干扰信号参数的情况下,多音干扰只能在信噪比十分低的情况下对直扩系统产生有效干扰。虽然在信噪比较低的情况下,其误码率较高,但是,一般来说,干扰一个脉冲调制的数字通信,只要其误码率达到10-3以上,其通信即不能完成。当信噪比大于10-1时,则连续可变增量调制的数字语音通信也不能正常通信,因此,大于10-1时,更高的误码率意义不大。反而,在信噪比较高的情况下,多音扫频干扰和单音扫频干扰依然能产生有效干扰。综合考虑,多音扫频干扰的效果要明显好于单音扫频干扰信号和多音信号。经过多次仿真实验,误码率的曲线与图5的仿真曲线基本一致。

图6 优化多音干扰频率时直扩系统误码率仿真Fig.6 Simulation of BER with better multi-tone jamming frequency for DSSS system

图6的仿真结果表明,多音干扰十分依赖频率引导,在干扰频率设置优化的情况下,其干扰效果明显。然而针对敌方直扩通信系统,很难在短时间内获得其系统参数,因此,要获得最佳多音干扰效果非常困难。综合来说,多音扫频干扰较前两种方法有明显的优势。

6 结束语

本文针对直扩系统的单音扫频信号和多音信号的干扰性能进行了分析,通过研究两种干扰方式各自的优缺点,扬长避短,提出了多音扫频干扰的方法,面对直扩系统的大带宽和载波频率难以获取的实际情况,该方法一方面不需要频率引导,减少了侦察的难度,克服了多音干扰存在的问题;另一方面,其通过多个音调的同时扫描,降低了扫频速率,干扰信号在目标频率附近的驻留时间增加,解决了单音扫频存在的问题。对该干扰方法的分析研究和仿真验证表明,该方法对于直扩系统的干扰能力明显优于已有的两种方法。

[1]Rodger E Ziemer,William H Tranter.Principles of CommunicationsSystems,Modulation andNoise[M].Beijing:Higher Education Press,2003.

[2]赵永宽,蔡晓霞,李鹏.DS系统的部分频段阶梯式线性扫频干扰性能分析[J].电子对抗,2010(5):19-22.ZHAO Yong-kuan,CAI Xiao-xai,LI Peng.Analysison PB Ladder-Like Liner Swept Jamming of DS System[J].Electronic Warfare,2010(5):19-22.(in Chinese)

[3]鲍晓利,冯永新.宽带扫频式干扰的仿真与FPGA实现[J].沈阳理工大学学报,2008(6):61-64.BAO Xiao-li,FENG Yong-xin.The Simulation and FPGA Realization of Broad Band Frequency Sweep Jamming[J].Transactions of Shenyang Ligong University,2008(6):61-64.(in Chinese)

[4]霍效新,刘剑锋,蒋卓勤,等.DS扩频系统的蒙特卡罗仿真及其音调干扰下的误码率分析[J].现代电子技术,2008(7):36-40.HUO Xiao-xin,LIU Jian-feng,JIANG Zhuo-qin,et al.Monte Carlo Simulationand BER Analysisof DS SpreadSpectrum System[J].Modern Electronic Technique,2008(7):36-40.(in Chinese)

[5]周扬,王昌宝,齐世友.音调干扰对超宽带通信干扰效果分析[J].通信对抗,2009(4):18-25.ZHOU Yang,WANG Chang-bao,QI Shi-you.Tone Jamming on UWBSystem and ItsEffect Analysis[J].Communica-tion Countermeasures,2009(4):18-25.(in Chinese)

[6]Richard A Poisel.Modern Communication Jamming Principles and Techniques[M].Beijing:Publishing House of Electronics Industry,2005.

[7]Peterson R L,Ziemer R E,Borth D E.Introduction to Spread Spectrum Communication[M].Upper Saddle River,NJ:Prentice Hall,1995:388.

[8]Torrieri D J.Principles of Secure Communication Systems[M].2nd ed.Norwood,MA:Artech House,1992:128.

[9]Milstein L B,Davidovice S,Schilling D L.The Effectof Multiple-Tone Interfering Signals on a Direct Sequence Spread Spectrum Communication System[J].IEEE Transactions on Communications,1982,30(3):436-448.