基于条件熵扩维的多变量混沌时间序列相空间重构*

张春涛 马千里 彭 宏 姜友谊

1)(重庆三峡学院数学与计算机科学学院，万州 404000)

2)(华南理工大学计算机科学与工程学院，广州 510006)

基于条件熵扩维的多变量混沌时间序列相空间重构*

张春涛马千里2)彭 宏2)姜友谊1)

1)(重庆三峡学院数学与计算机科学学院，万州 404000)

2)(华南理工大学计算机科学与工程学院，广州 510006)

(2010年4月12日收到;2010年5月22日收到修改稿)

提出一种多变量混沌时间序列相空间重构的条件熵扩维方法.首先使用互信息法求解每个变量的时间延迟，其次按条件熵最大原则逐步扩展相空间的嵌入维数，使得重构坐标从低维到高维的转换保持较强的独立性，最终的重构相空间具有较低的冗余度，为多变量时间序列的预测构造了有效的模型输入向量.通过对几个经典多变量混沌时间序列进行数值实验，结果表明该方法比单变量预测和已有多变量预测方法具有更好的预测效果，说明了该重构方法的有效性.

多变量混沌时间序列，相空间重构，条件熵，神经网络预测

PACS:05.45.Pq，05.45.Tp

1.引 言

复杂系统中任一分量的演化都可由系统的其他分量所决定，因此任一分量的发展过程都包含其他分量的信息，即通过该分量发展的时间序列重构相空间能充分反映原系统的动力学特征，这就是单变量混沌时间序列相空间重构［1—8］.在现实状况下由于无法从单变量的时间序列获全系统信息，以及在分析生物学系统时，由于其结构和动力系统的复杂性，很难由一维时间序列通过延迟嵌入法重构出相空间［9］，因此不能保证实际系统中任何给定的单变量时间序列足以重构原系统［10，11］.而多变量时间序列由于包含了更丰富完整的系统信息，故能重构出更为准确的相空间，因此多变量混沌时间序列的研究得到越来越多的关注［12—18］.

目前，对多变量时间序列已取得了许多研究成果.王海燕等［14］提出由单变量推广的虚假邻近点法计算多变量时间序列的相空间嵌入维数，但其缺少每次扩维选择标准，使重构相空间具有不定性. Broomhead等［15］提出奇异值分解法求取多变量时间序列的嵌入维数.Cao等［10］对多变量的相空间重构问题进行理论和应用研究，并论证了其优越性;樊重俊［16］讨论了多观测变量状态空间重构技术，为研究多变量时间序列的相空间重构提供了理论基础.

信息熵是系统整体不确定性的一种量度，在混沌时间序列相空间重构中有重要应用.田玉楚等［19］系统地论述了在不变测度意义下，将混沌系统视为一类特殊的随机系统加以处理;肖方红等［6］对一维时间序列使用条件熵求取相空间的嵌入维数;我们也研究了两个重构参数的信息熵模型［8］.这些研究都集中在单变量混沌时间序列上，对多变量混沌系统，主要用互信息法求解单个变量的延迟时间.

本文沿用单变量时间序列建模的思想，结合信息熵和神经网络对多变量时间序列进行相空间重构和预测，提出了多变量混沌时间序列的条件熵扩维方法(CEED).首先使用互信息法求解单个变量的时间延迟;然后使用条件熵扩维方法，按条件熵最大原则选择重构分量，把低维相空间逐渐扩展到高维相空间，使得最终的相空间具有较少的冗余度.为了检验该重构方法的有效性，最后使用神经网络对2个典型的多变量混沌系统进行仿真实验，数值实验表明在该重构方法上进行的多变量混沌时间序列预测能取得比单变量和已有的多变量预测更好的效果，说明CEED方法重构了高质量的相空间.

2.多变量混沌时间序列相空间重构

在一定程度上单变量时间序列是多变量时间序列的特殊情况，因此可将单变量的延迟重构应用到多变量中.对单变量时间序列x(n)(n=1，2，…，N)，在确定嵌入维数 m和时间延迟 τ后，重构相空间

设复杂系统的N维多观测变量序列为 X1，X2，…，XK，其中 K表示观测变量个数，Xi=［xi(1)，xi(2)，…，xi(N)］表示第i个变量的时间序列.如果每个变量都选择恰当的时间延迟τi和嵌入维数mi(i=1，2，…，K)，则多变量时间序列重构的相空间

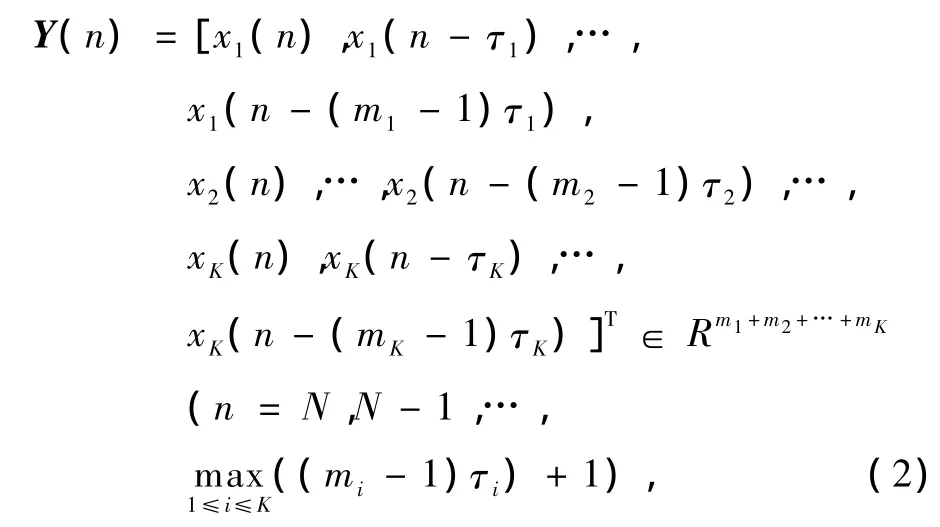
其中τi和mi是重构相空间成败的关键，目前还没有一个统一的选择标准，下面使用信息论知识来选择这K对重构参数.

2.1.多变量时间序列延迟时间的选择

设两个离散型随机变量X∈{x1，x2，…，xn}和Y∈{y1，y2，…，yk}，其 先 验 概 率 分 别 为 {p (xi)}i=1，2，…n和{p(yj)}j=1，2，…，k.信息熵可定义为

它描述了随机变量X的不定性.类似地可以定义联合熵

其中p(xi，yj)为联合概率.

变量X和Y之间的互信息定义为

根据(7)式可推出时间序列和其延迟时间序列的互信息

根据互信息法［5］，计算出互信息函数 I(τi)在不同延迟τi下的值，取I(τi)的第一个局部极小值点对应的时间τi为第 i个变量时间序列 Xi的延迟时间.

2.2.多变量时间序列嵌入维数的确定

一般认为，如果重构相空间的维数足够大，相空间就能够刻画出原系统的吸引子.对多变量时间序列，一个很自然的想法就是对每个变量的时间序列都分别求一个嵌入维数mi，然后将所有变量的重构相空间进行简单迭加形成多变量时间序列的相空间如(2)式.由于混沌系统任一变量的时间序列包含其他变量的信息，即使单个变量的重构相空间无冗余信息，经过简单迭加而成的多变量时间序列的重构相空间也包含大量的冗余信息，不利于预测.如何减少这些冗余信息，是确定多变量时间序列嵌入维数的关键.主成分分析(PCA)方法［17，18］为我们提供了一种解决途径，但是PCA方法只能消除各重构分量间的线性关系，对非线性的时间序列作用有限.下面根据条件熵能反映变量之间的独立性的特征，通过条件熵消除各重构分量间的非线性关系，使重构相空间包含较少冗余信息，以达到降低相空间维数的目的.

记多变量重构相空间(2)式的延迟坐标向量的各分量为

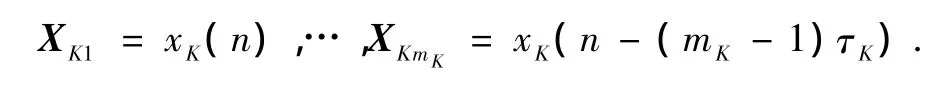
相空间重构也就是用重构分量 X11，X12，…，XK1，XK2，…，XKmK近似表征原系统的各变量，同时X11，X12，…，XK1，XK2，…，XKmK也可以看成是重构相空间的坐标，因此原系统表现出来的混沌吸引子也将在重构分量X11，X12，…，XK1，XK2，…，XKmK的重构相空间中表现出来.这样随着重构分量的逐渐增多，重构向量就能越来越完整地表征原系统的动力学特征.当重构的分量个数增加到一定值时，这时重构的分量包含了原系统充分多的动力学信息，进一步增加重构分量不会增加原系统的动力学信息，只会携带冗余信息.因此可以设想分量X11，X21，…，XK1的熵H(X11，X21，…，XK1)和各分量之间的条件熵的值随着重构分量个数的增加由大到小逐渐减小，直至重构分量包含充分多的原系统的动力学信息，进一步增加重构分量个数，这时条件熵将出现一个较明显的转折点，随后的条件熵将趋于平稳.如果取条件熵出现较为明显的转折且趋于平稳处的重构分量个数作为多变量时间序列重构相空间的嵌入维数，可以看出此时重构向量已包含原系统充分多的动力学信息，应该是一个合适的嵌入维数［6］.

多变量时间序列的重构向量中增加一个重构分量有诸多选择，即在已知重构分量为 X11，X12，X21的条件下再增加一个分量，有 K种不同选择:X13，X22，X31，X41，…，XK1.对这 K个条件熵做怎样的取舍?由上所述，多变量时间序列重构相空间应具有较少的冗余信息，即重构分量之间应最大限度地相互独立.因此增加一个重构分量的最佳选择应是K个条件熵的最大值所对应的分量.因为条件熵最大，表明增加的这个分量和原有分量的独立性最大，这样不断增加重构分量到整个相空间就能够保证有最大的独立性.下面给出从低维到高维的扩维(增加相空间重构分量个数)算法步骤:

步骤1 对每个变量的时间序列使用互信息法求时间延迟τi，i=1，2，…，K;

步骤2 初始化:令Y=［X11，X21，…，XK1］为初始的重构向量，每个变量的初始嵌入维数mi=1，i= 1，2，…，K;

步骤3 计算条件熵并扩维:

3)扩维mk=mk+1，此时的重构向量 Y=［Y，Xkmk］;

4)重复1)—3)直至最大条件熵趋于平稳.

步骤4 循环结束后的重构向量空间就是多变量时间序列的重构相空间，此时的mi即为第i观测变量的嵌入维数，重构相空间的嵌入维数m=m1+ m2+…+mK.

对条件熵按(6)式转化为联合熵来计算，本文采用矩阵标识法［6］计算联合熵.

3.多变量混沌时间序列仿真实验

为了验证 CEED的有效性，我们做了 Henon，Lorenz系统的单步和多步预测实验，并与现有的单变量和多变量预测方法进行比较.

3.1.预测模型的建立

假设重构的状态空间如(2)式，相空间中预测的基本思想是:根据历史状态数据集建立第 i时刻状态Y(i)到第i+h时刻状态Y(i+h)的映射Fh，然后由映射Fh和当前n时刻状态Y(n)去推断未来n+h时刻状态Y(n+h)的估计值Z(n+h)，其中h为预测步长.根据嵌入定理，状态映射Fh是存在的，即在m维的重构相空间存在光滑函数fh:Rm→R.对多变量混沌时间序列，因此有预测模型

其中，zi(n+h)为模型对未来(n+h)时刻第i个变量状态xi(n+h)的预测值(i=1，2，…，K)，h为预测步长.由于混沌系统的高度非线性，要确定函数fih的解析形式是困难的，我们采用神经网络的学习原理来逼近这些映射函数.结合相空间重构和神经网络建立预测模型的结构如图1所示.

图1 多变量时间序列预测模型结构

本文采用的神经网络是 Elman递归神经网络［20］，它能够通过内部的递归连接反映非线性动力系统的特征，在混沌时间序列的预测中有重要应用［2，3］.

3.2.仿真实验

为了评价预测效果采用均方误差(MSE)、均方根误差(RMSE)、标准化均方误差(NMSE)以及绝对误差e(t)作为误差评价标准:

3.2.1.Henon混沌时间序列

法国天文学家Henon于1976年提出一个简单的二维平方映像如下:

通过计算得出变量x，y的3000个点的数据集，使用互信息法分别求解x和y的延迟时间如图2和图3所示，可知τ1=15，τ2=14，然后通过条件熵扩维如图4所示.

由图4可知，在嵌入维数为5时条件熵出现一个明显的转折，当嵌入维数增加到6后条件熵几乎不发生变化，所以我们取Henon重构相空间的嵌入维数为6，再根据每次的重构分量选择m=m1+m2=4+2=6.

通过Elman神经网络按(9)式对变量x进行预测.前2000个数据点进行训练，后1000个数据进行预测，其中单步预测结果与单变量预测方法:在线最小二乘支持向量机(LS-SVM)［21］，最小二乘支持向量(LS-SVD)［22］，模糊树Ⅰ(FTⅠ)［23］，FTⅡ［23］，模糊聚类［24］，基于自适应网络的模糊推理系统(ANFIS)［25］，局域离散余弦变换领域Vloterra(LDCTDV)［26］，模糊边界模块化神经网络 FBMNN［2］以及多变量预测方法的比较如表1所示，其中非线性独立分量分析(NICA)为文献［27］所取的多变量相空间结构:m1=2，τ1=1;m2=2，τ2=1，然后使用Elman神经网络的预测.

图2 x的互信息

图3 y的互信息

图4 条件熵与嵌入维数的关系

从表1可以看出CEED取得比单变量预测和多变量预测更好的预测效果.单步预测效果和预测误差分别如图5和图6所示.

从图6可以看出，对Henon混沌时间序列的单步预测误差达到10-5数量级，比文献［28］的10-2高3个数量级，说明使用多变量时间序列预测 Henon是高效.

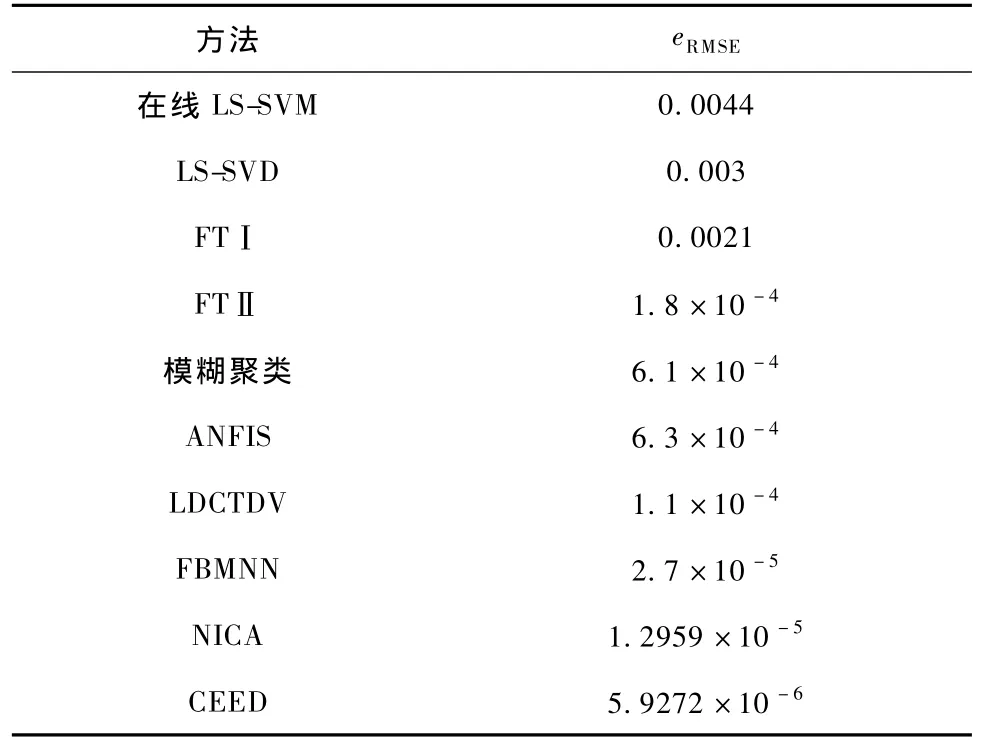
表1 单步预测

图5 单步预测效果

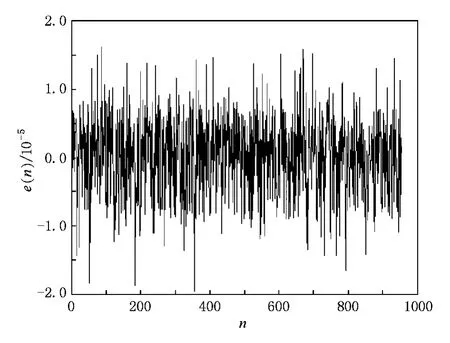
图6 单步预测误差

在进行的多步预测中，预测结果与正交最小二乘径向基函数(RBF(OLS))［29］，局域线性模型树(LoliMoT)［29］，FBMNN和NICA的比较如表2所示，其中节点数为隐含层节点数.

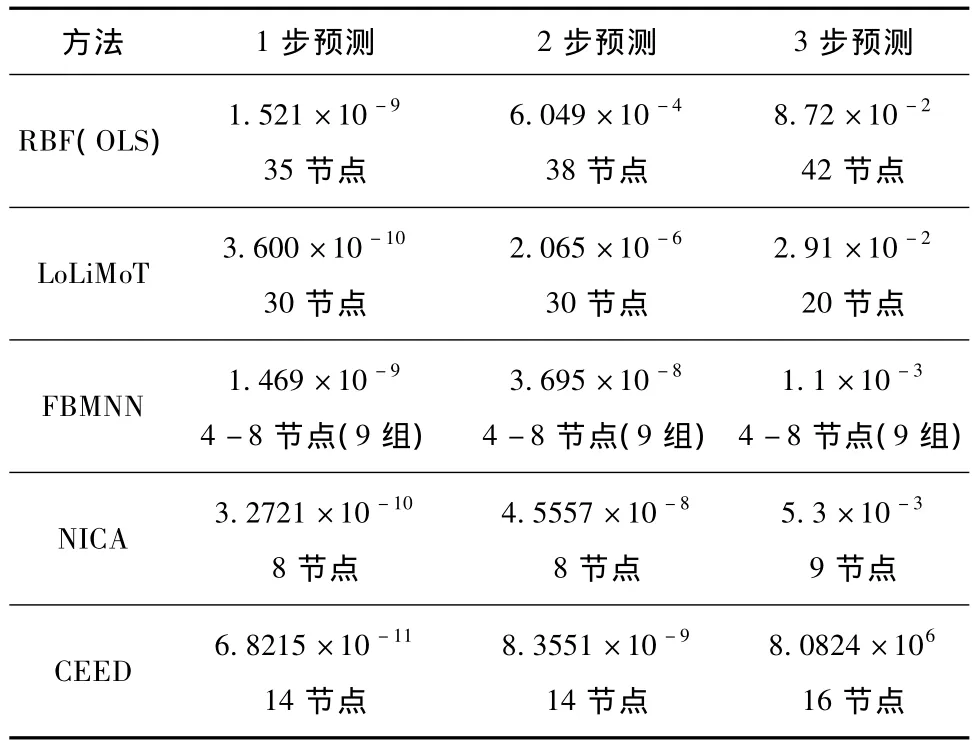
表2 Henon预测结果的NMSE比较

由表2可以看出CEED使用较少的隐含层节点，从而降低了计算复杂性，却能取得更好的预测效果.

从表1和表2可以看出，Henon映像是一个最简单的二维混沌系统，使用单变量预测方法和已有的多变量相空间重构方法进行单步预测大多能取得较好的预测效果，但多步预测效果一般较差，而使用CEED的多变量预测方法在单步和多步预测上都取得了很好的预测效果.FBMNN，NICA和CEED都使用Elman进行预测，CEED上进行的预测取得了最好的预测效果，说明了 CEED重构方法对Henon映像的有效性.

3.2.2.洛伦兹方程

洛伦兹方程如下:

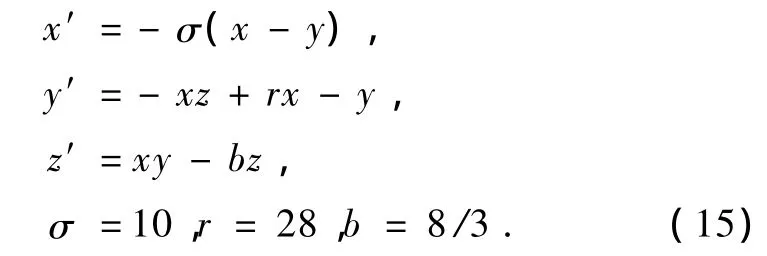
用四阶Runge-Kutta方法求解方程(15)，取积分步长h=0.02，得到变量x，y的两个7500个点的数值解，去除前5000个点的暂态过程，最后考虑两个观察变量x，y的2500个点的数据集，将其归一化到［0，1］区间.先通过互信息法分别求出x和y的延迟时间如图7和图8所示，由图7，图8可知，τ1=8，τ2=8.

然后通过条件熵扩维如图9所示，由图9可知，当嵌入维数增加到6后条件熵不再发生变化，再根据扩维分量选择有m=m1+m2=2+4=6.

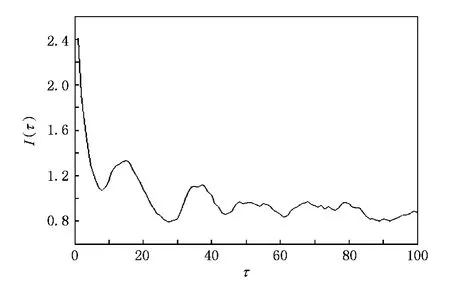
图7 x的互信息

图8 y的互信息

图9 条件熵与嵌入维数的关系

通过Elman神经网络按(9)式对变量x进行预测.前2000个数据点进行训练，后500个数据进行预测，其中单步预测结果与单变量时间序列预测和多变量预测的比较如表3所示，其中IFNNMU为单变量推广的虚假邻近点法确定的相空间结构:m1= 2，τ1=8;m2=1，τ2=8，然后使用Elman神经网络的预测.

从表3可以看出，对Lorenz系统CEED能取得比已有的单变量时间序列预测和多变量预测更好的单步预测效果.

为了与多变量预测方法［30］进行比较，将归一化数据还原为原始数据，根据eRMSE的定义有，对Lorenz系统归一化数据后的 eRMSE是原始数据的 1/40，即CEED原始数据的 eRMSE≤2×10-5，比文献［30］的0.063高3个数量级.CEED的嵌入维数是6，而文献［30］的嵌入维数为11，这样CEED能简化神经网络结构，更利于实现.

单步预测效果如图10所示，预测误差如图11所示.

图10 单步预测效果

图11 单步预测误差

同时我们也进行了多步预测实验，预测步长取为6和8，与共进化递归神经网络(CERNN)［3］等相关预测方法的比较如表4和表5所示.

表4 6步预测

表5 8步预测

从表4和表5可以看出，对Lorenz系统，在CEED上进行的多步预测精度也高于单变量预测和多变量预测方法.从表 3—表 5可看出，FBMNN，CERNN，IFNNMU和CEED都使用了Elman网络进行预测，在CEED重构相空间上进行的预测取得了更好的预测效果，说明CEED重构方法对Lorenz系统的有效性.

从表1—表5可以看出，对多维混沌系统，不管是与单变量时间序列预测方法，还是与已有的多变量预测方法相比，CEED重构相空间上进行单步和多步预测都能取得更好的预测效果，说明CEED重构的多维混沌系统的相空间是有效性.

4.结 论

本文提出一种多变量混沌时间序列相空间重构的新方法.该方法通过条件熵扩张相空间维数，按条件熵最大选择重构分量，使得相空间从低维到高维的转变过程中既保证重构坐标的独立性又保持系统的动力学特征.因此通过CEED确定的重构相空间既能充分包含系统信息，又能有效避免冗余信息的产生.最后在CEED上进行多变量混沌时间序列的单步和多步预测，都取得了比使用单变量预测方法和已有的多变量预测方法更好的预测效果，表明CEED重构方法的有效性.

［1］Peng S G，Yu S M 2009 Chin.Phys.B 18 3758

［2］Ma Q L，Zheng Q L，Peng H，Qin J W 2009 Acta Phys.Sin.58 1410(in Chinese)［马千里、郑启伦、彭 宏、覃姜维2009物理学报58 1410］

［3］Ma Q L，Zheng Q L，Peng H，Zhong T W，Qin J W 2008 Chin. Phys.B 17 536

［4］Zhang S Q，Jia J，Gao M，Han X 2010 Acta Phys.Sin.59 1576 (in Chinese)［张淑清、贾 健、高 敏、韩 叙 2010物理学报59 1576］

［5］Fraser A M，Swinney H L 1986 Phys.Rev.A 33 11340

［6］Xiao F H，Yan G R，Han Y H 2005 Acta Phys.Sin.54 550(in Chinese)［肖方红、阎桂荣、韩宇航2005物理学报54 550］

［7］Yan H，Wei P，Xiao X C 2009 Chin.Phys.B 18 3287

［8］Zhang C T，Ma Q L，Peng H 2010 Acta Phys.Sin.7623(in Chinese)［张春涛、马千里、彭 宏2010物理学报7623］

［9］Kantz H，Schreiber T 1997 Nonlinear Time Series Analysis (Cambridge:Cambridge University Press)p7

［10］Cao L Y，Mees A，Judd K 1998 Physica D 121 75

［11］Rombowts S A R B，Keunen R WM，Stom C J 1995 Phys.Lett. A 202 352

［12］Lu S，Wang H Y 2006 Acta Phys.Sin.55 572(in Chinese)［卢 山、王海燕2006物理学报55 572］

［13］Zhang Y，Guan W 2009 Acta Phys.Sin.58 756(in Chinese)［张 勇、关 伟2009物理学报58 756］

［14］Wang H Y，Sheng Z H，Zhang J 2003 J.Southeast Univ. (Natural Science Edition)33 115(in Chinese)［王海燕、盛昭瀚、张 进2003东南大学学报(自然科学版)33 115］

［15］Broomhead D S，King G P 1986 Physica D 20 217

［16］Fan C J 2009 J. UniversityofShanghaiforScienceand Technology 31 273(in Chinese)［樊重俊2009上海理工大学学报31 273］

［17］Han M，Fan M M，Xi J H 2005 Lecture Notes in Computer Science 3497 618

［18］Han M，Wang Y 2009 Expert Systems with Applications 36 1280

［19］Tian Y C，Fu X T，Lu Y Z 1993 Control and Decision 8 345(in Chinese)［田玉楚、符雪桐、吕勇哉1993控制与决策8 345］

［20］Elman J L 1990 Cognitive Science 14 179

［21］Ye M Y，Wang X D，Zhang H R 2005 Acta Phys.Sin.54 2568 (in Chinese)［叶美盈、汪晓东、张浩然 2005物理学报 54 2568］

［22］Ren R，Xu J，Zhu S H 2006 Acta Phys.Sin.55 555(in Chinese)［任 韧、徐 进、朱世华2006物理学报55 555］

［23］Mao J Q，Yao J，Ding H S 2009 Acta Phys.Sin.58 2220(in Chinese)［毛剑琴、姚 健、丁海山2009物理学报58 2220］

［24］Chiu S 1994 J.Intell.Fuzzy Syst.2 267

［25］Jang J S R 1993 IEEE Trans.Syst.Man 23 665

［26］Zhang J S，Li H C，Xiao X C 2005 Chin.Phys.14 49

［27］Jan S，Guatavo D 1997 Physics D 108 335

［28］Zhang J F，Hu S S 2008 Acta Phys.Sin.57 2708(in Chinese)［张军峰、胡寿松2008物理学报57 2708］

［29］Gholpour A，Araabi B N，Lucas C 2006 Neural Proc.Lett.24 217

［30］Han M，Wei R 2008 14th International Conference of Neural Information Processing Kitakyushu，Japan，November 13—16，2007 p415

PACS:05.45.Pq，05.45.Tp

Multivariate chaotic time series phase space reconstruction based on extending dimension by conditional entropy*

Zhang Chun-TaoMa Qian-Li2)Peng Hong2)Jiang You-Yi1)
1)(College of Mathematic and Computer Science，Chongqing Three Gorges University，Wanzhou 404000，China)
2)(College of Computer and Engineering，South China University of Technology，Guangzhou 510006，China)

12 April 2010;revised manuscript

22 May 2010)

For multivariate chaotic time series，a method of conditional entropy extending dimension(CEED)in the reconstructed phase space is proposed.First，the delay time of any variable time series is selected by mutual information method，and then the embedding dimension of phase space is extended by the conditional entropy.This method can ensure the independence of reconstructed coordinates from low space to high space and eliminate the redundancy of phase space，because the largest condition entropy is choosen.The effective input vector for the prediction of multivariate time series is given.Simulations of the Lorenz system and Henon system show that the neural network predictions of multivariate time series are much better than the prediction of univariate and existing multivariate.Therefore，CEED is effective for multivariate chaotic systems.

multivariate chaotic time series，phase space reconstruction，conditional entropy，neural network prediction

*广东省自然科学基金(批准号:9451064101003233)、华南理工大学中央高校基本科研业务费专项资金(批准号:2009ZM0125，2009ZM0189，2009ZM0255)和重庆三峡学院重点项目(批准号:10ZD-16)资助的课题.

*Project supported by the Natural Science Foundation of Guangdong Province，China(Grant No.9451064101003233)，the Fundamental Research Funds for the Central Universities，South China University of Technology(Grant Nos.2009ZM0125，2009ZM0189，2009ZM0255)and the Key Program of the Chongqing Three Gorges University，China(Grant No.10ZD-16).