Dicke模型的量子经典对应关系*

宋立军 严 冬 盖永杰 王玉波

1)(长春大学理学院，长春 130022)

2)(长春理工大学理学院，长春 130022)

Dicke模型的量子经典对应关系*

宋立军严 冬1)盖永杰1)王玉波2)

1)(长春大学理学院，长春 130022)

2)(长春理工大学理学院，长春 130022)

(2010年3月22日收到;2010年5月3日收到修改稿)

非旋波近似条件下Dicke模型表现为量子混沌动力学特征.在详细考察Dicke模型经典相空间结构特点的基础上，采用经典-量子“一对多”的思想，即经典相空间中的一点对应于量子体系两个初始相干态的演化，利用对两个初态量子纠缠动力学演化取统计平均的方法，得到了与经典相空间对应非常好的量子相空间结构.数值计算结果表明:经典混沌有利地促进系统两体纠缠的产生，平均纠缠可以作为量子混沌的标识，利用平均纠缠可以得到一种较好的量子动力学与经典相空间的对应关系.

Dicke模型，非旋波近似，量子混沌，经典量子对应

PACS:03.65.Ud，03.67.Hk，05.45.Mt，42.50.Dv

1.引 言

自然界中的混沌是普遍存在的，并且在许多科学领域都扮演了重要的角色［1，2］.在经典物理学中，混沌可以由系统对初始条件的敏感性来刻画.在量子力学中，根据玻尔的对应原理，量子力学应用到宏观运动上所得到的结果应该与经典力学的结果一样.因此，经典力学中的混沌特征也必然要在其量子性质上有所表现.自从20世纪中期以来，人们在许多非线性系统中发现了量子混沌并逐渐认识到其重要性.但是，由于不确定关系，在量子力学中并不能像经典力学那样对系统的运动做确定性的相空间描述，所以，有关经典混沌的量子标识问题和量子经典对应关系的研究充满了挑战性.近年来，随着量子信息科学的发展，人们开始尝试利用一些量子信息概念来理解量子混沌并取得了一些丰硕的研究成果.例如量子关联或纠缠［3—13］、保真度［14—16］和自旋压缩［17—20］等，这些成果揭示了量子动力学过程中混沌行为存在的本质，特别是有关量子混沌中纠缠性质成为人们的研究热点之一.其根本原因在于纠缠是量子力学的核心和量子信息过程的一种重要资源，因此可以将纠缠作为量子混沌的一种标识，从而为量子混沌研究提供一种有效方法.Furuya等［3］研究 N个原子的 Jaynes-Cummings模型时发现，当系统处于经典混沌轨道，原子与光场之间线性熵的增长率比系统处在规则轨道时要大.在2009年的一期《Nature》杂志上，Chaudhury等［21］报道了实现有关量子混沌的一种实验.他们在量子受击陀螺模型中，利用纠缠作为量子混沌的标识，发现量子纠缠动力学与经典相空间结构之间具有一种非常好的对应关系.那么，对于描述光与物质相互作用系统的 Dicke模型［22］，由于非旋波近似条件下也表现为量子混沌动力学性质，是否在经典相空间结构与量子动力学之间也存在着这种较好的量子经典对应关系呢?本文在对非旋波近似条件下 Dicke模型经典相空间结构进行详细考察后，发现经典相空间的任意一点与量子系统的两个初始相干态相对应，利用对两个初态的纠缠动力学演化取统计平均的方法，定义平均线性熵概念，得到了一种非常好的量子经典对应关系，从而为腔场中量子混沌实验的实现提供一种新的思路.

2.Dicke模型

一般而言，Dicke模型是描述N个二能级原子与n模光场相互作用的典型理论模型.它在许多物理研究领域具有重要应用，例如原子核物理、量子混沌以及量子耗散等.本文只考虑N个二能级原子(量子比特)和一个单模辐射场相互作用情况，通过改变耦合系数来实现旋波近似和非旋波近似.忽略原子(量子比特)之间的相互作用，将原子系统作为一个大的自旋系统(N=2j)来处理.这时Dicke模型的哈密顿量可以写成下列形式［4］:

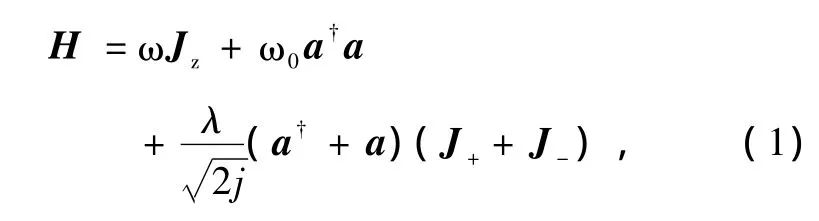
式中ω和ω0分别是N个二能级原子的跃迁频率和单模光场的频率;λ是原子与场相互作用过程中的耦合系数;a，a是光场的湮灭和产生算符;Jz，J±是与原子的可观测量有关的赝自旋算符，它们满足SU (2)李代数

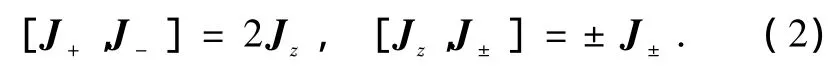
利用哈密顿量(1)式可以研究系统的纠缠动力学性质.但一个首要问题是如何选择初始的量子态.这里，我们为了考察Dicke模型经典相空间结构与量子纠缠动力学之间的对应关系，可以通过选择相干态作为初态来实现，即最小不确定波包中心集中在对应的经典相空间中.初始量子态选择如下:

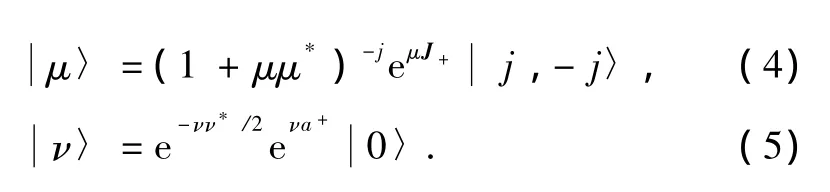
其中

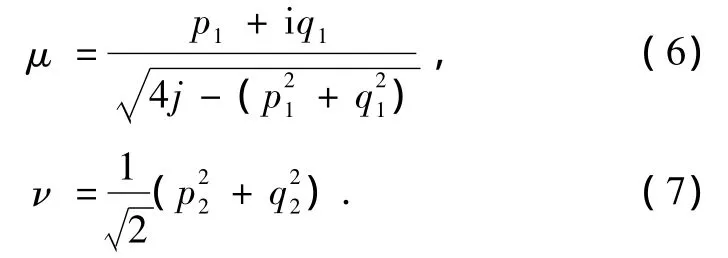
为了得到与(1)式相对应的经典哈密顿量，从而更直观地研究混沌动力学过程，利用 Holstein-Primakoff变换将Dicke模型的量子哈密顿量转换为相应的经典哈密顿量［23］

上式对应的哈密顿运动方程可以表示为

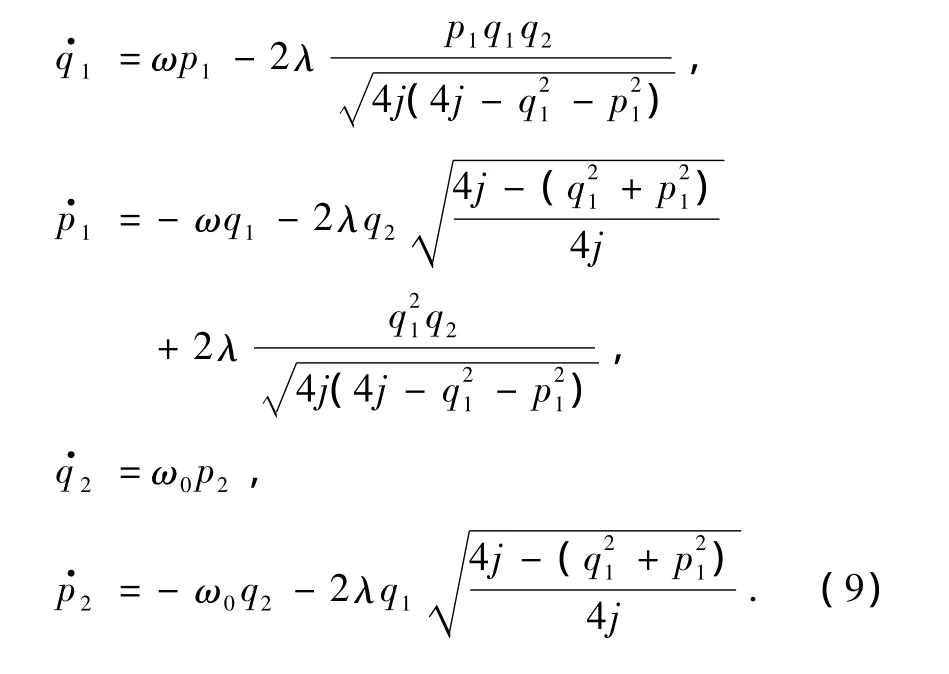
3.经典相空间结构

根据经典动力学方程(9)，通过数值模拟计算，得到经典相空间的庞加莱截面图.以往绝大多数研究工作都将四维相空间庞加莱截面降维到二维平面［5］，即只取(p1，q1，p2，q2)四个量中 q2=0，p2>0情形的庞加莱截面图进行研究［2—4］.本文的目的是考察Dicke模型中经典相空间结构与量子纠缠动力学性质之间的对应关系，所以首先将四维相空间庞加莱截面降维到三维空间，即只取q2=0情形，得到系统整体三维庞加莱截面如图1所示.三维庞加莱截面图显示包含有两个子庞加莱截面图，他们的空间结构具有以下明显特点:1)每个子截面图都有两个较大的规则区和一些小的规则区域，这些区域具有周期性轨道的稳定运动，区域的中心一般为不动点，规则区域外为混沌区域，运动是不稳定的;2)两个子截面图分别代表 Dicke模型p2>0和 p2<0情形的经典相空间，而且它们以 p2=0为轴具有反对称性;3)每个子截面图都是以q1=0为轴对称的.以上这些特点对于分析系统整体量子纠缠动力学与经典相空间之间的对应关系是至关重要的.

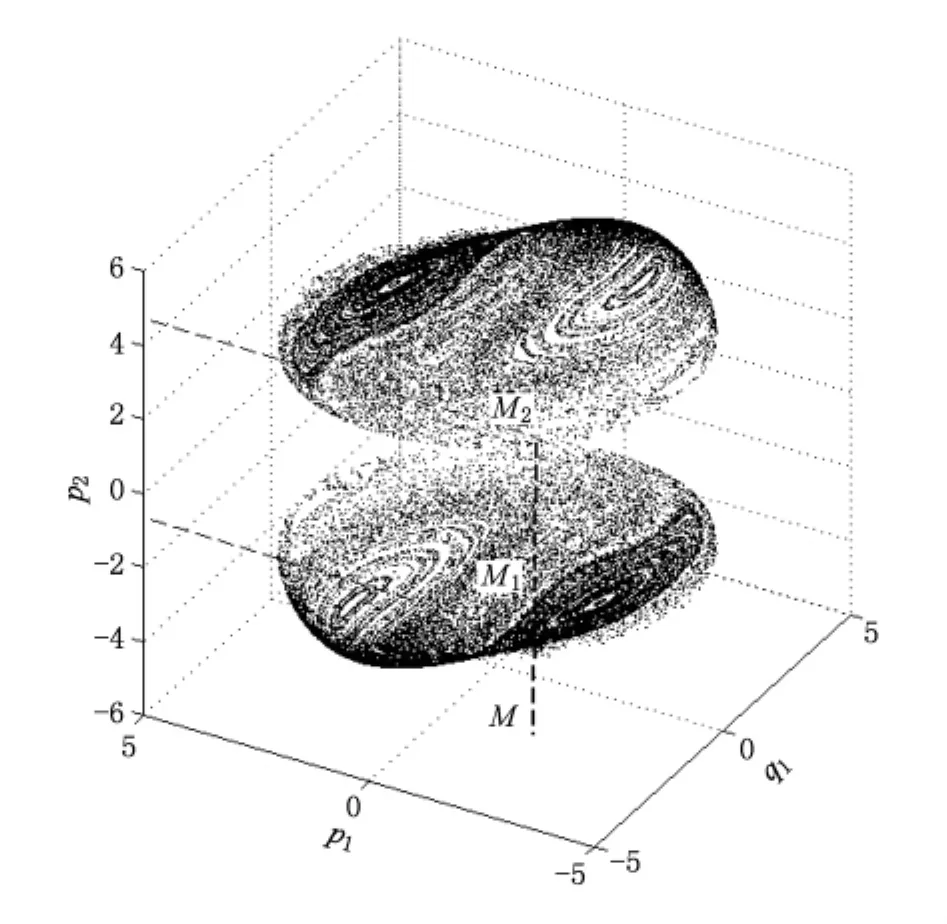
图1 经典相空间的三维庞加莱截面图 (参数分别为 ω=ω0=1，E=8.5

在图1中我们可以清楚地看到，对于每个子截面图而言，在上面任取一点都对应于一组确定的(p1，q1，p2)值，但是如果考察Dicke模型整个体系的相空间结构，需要将两个子截面图作为一个整体进行分析.这时可以发现，在图1中(p1，q1)平面内任取一点分别对应于每个子截面上的一点.例如取(p1，q1)平面内一点M，则分别对应于两个子截面图上的M1和M2两个点，即确定一个(p1，q1)值后，p2应该分别取p2>0和p2<0两个值.所以，在量子系统动力学演化过程中，(6)式中经典相空间(p1，q1)取某个确定值μ后，则一定要对应(7)式ν(p2>0)和ν(p2<0)两个值，将它们分别代入(3)—(5)式得到量子体系动力学演化的两个初态.以上分析说明，考察Dicke模型中经典混沌对量子体系的影响，取每个子庞加莱截面图经典相空间上的一点作为初始条件，必须对应两个初始相干态的量子动力学演化，这样才能完整地描述整个物理系统的量子力学性质.这种“一对多”现象经常出现在经典物理与量子力学之间.例如，如果两个经典力学量之间满足对易关系，则一个经典哈密顿量可以对应两个量子哈密顿量.

4.平均纠缠动力学

在详细分析Dicke模型经典相空间的结构特点后，下面我们利用约化密度线性熵来考察系统的纠缠动力学演化性质，尝试找到一种好的量子经典对应关系.

纠缠线性熵定义如下［18］:

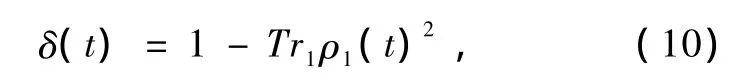
这里，Tr1表示对第一个子系统取迹，ρ1(t)=是约化密度矩阵，其中下角标1和2分别表示原子和辐射场子系统，ψ(t)是整个系统的量子态.

为讨论问题的方便，我们将图1中的三维庞加莱截面图重新降维为二维平面图，如图2所示.其中，图2(a)代表p2>0子庞加莱截面图，图2(b)代表p2<0子庞加莱截面图.在图2(a)中分别取p1= 2.2，p1=0，p1=-3.2三条直线穿过经典相空间两个较大的规则区域和混沌海区域.由于每个子庞加莱截面图是关于q1=0左右对称的，分别在三条直线上q1=0左右两边对称取两点q1=-1.0和q1= 1.0考察纠缠动力学的演化规律.数值模拟计算结果见图3.

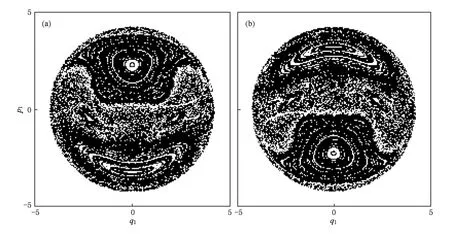
图2 经典相空间的二维庞加莱截面图 (a)p>0情形，(b)p<0情形(参数分别为ω=ω=1，E=8.5，λ220=0.32)

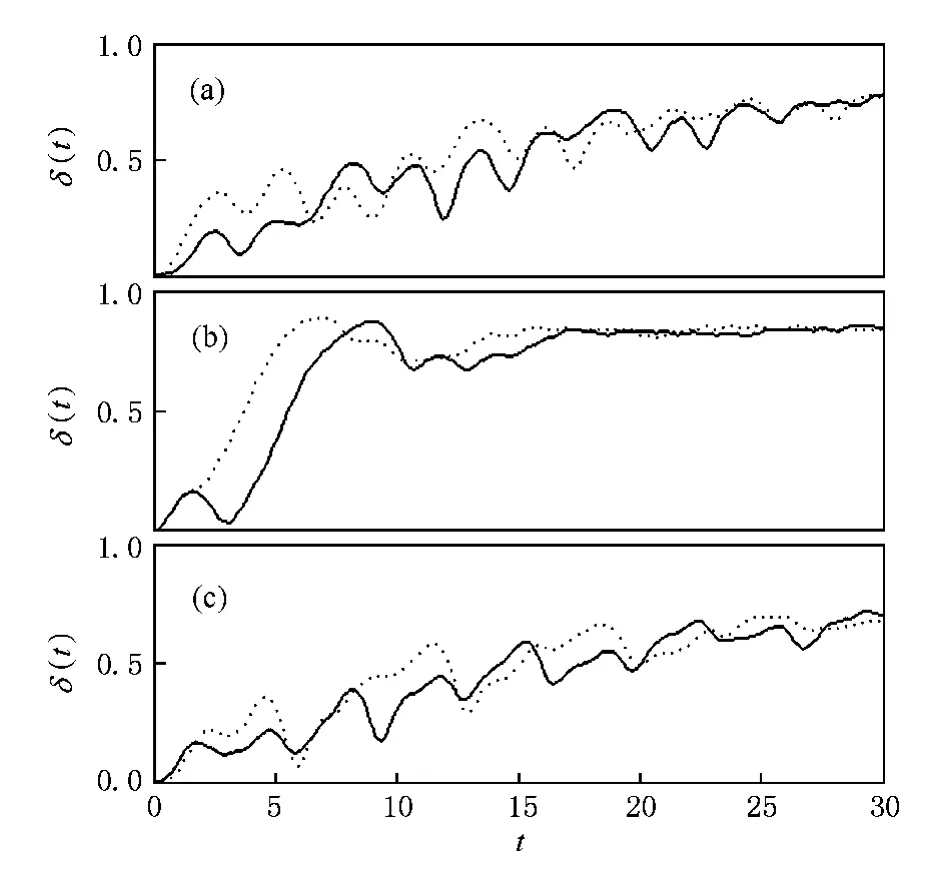
图3 经典相空间对称点纠缠动力学演化曲线 (a)实线代表初始点为(p1=2.2，q1=1.0)，虚线代表初始点为(p1=2.2，q1=-1.0);(b)实线代表初始点为(p1=0，q1=1.0)，虚线代表初始点为(p1=0，q1=-1.0);(c)实线代表初始点为(p1=-3.2，q1=1.0)，虚线代表初始点为(p1=-3.2，q1=-1.0) (其他参数同图1)

由图3可以明显发现，在经典相空间无论规则区域和混沌区域，取对称两点作为量子动力学演化的初态，线性熵的变化曲线都是不相同的，存在着一定的差异，说明量子相空间纠缠动力学不具有对称性.造成这一差异的主要原因就是前面对经典相空间结构分析中所指出的，动力学演化过程中初态选择具有经典量子“一对多”的特点.为了解决这个问题，得到较好的量子动力学与经典相空间的对应关系，下面我们定义平均线性熵来描述量子纠缠动力学的演化特点.平均线性熵定义如下:

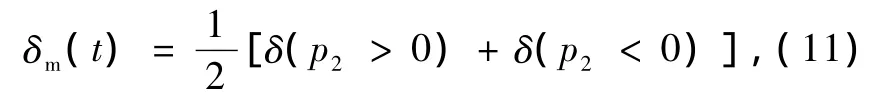
其中，δ(p2>0)和δ(p2<0)分别表示体系任取一组(p1，q1)初始值，对应每个子庞加莱截面图上一个初始值作为初态的线性熵.利用这种方法，我们以图2(a)所示的子庞加莱截面图为例，重新考察 p1分别取2.2，0和 -3.2时，纠缠动力学演化关于 q1=0的对称性，数值模拟计算平均线性熵δm(t)随q1的变化曲线如图4所示.

图4 对应子庞加莱截面图2(a)平均线性熵δm(t)随q1变化曲线 (a)p1=2.2，(b)p1=0，(c)p1=-3.2(其他参数同图1)

由图4可以发现，在三个不同的区域，平均线性熵δm(t)关于q1=0都具有非常好的对称性(这里应该注意，图4(a)—(c)三个子图的横坐标是不同的).在图4(a)中，我们发现在q1=0处存在一个δm(t)极小值，正好对应经典子庞加莱截面图2(a)中较大的规则区域，而极小值两侧的曲线逐渐增大，较好地刻画了规则区域经周期性轨道过渡到混沌区域的变化;图2(a)中p1=0这条直线是贯穿于混沌区域的，所以δm(t)值应该较大，在图4(b)给出的曲线值较大且形状非常平缓，很好地反映了经典相空间的结构;当p1=-3.2时，该直线贯穿于另一个较大的规则区域，而图4(c)中的δm(t)曲线在中间刚好出现一段平缓部分，对应于图2(a)中的规则区域.通过以上分析，我们发现在系统经典相空间与量子纠缠动力学演化之间存在一种非常好的对应关系，利用平均线性熵可以有效地标识量子混沌，而且经典混沌是促进系统原子与光场之间纠缠产生的，这一结论与文献［2］是一致的.

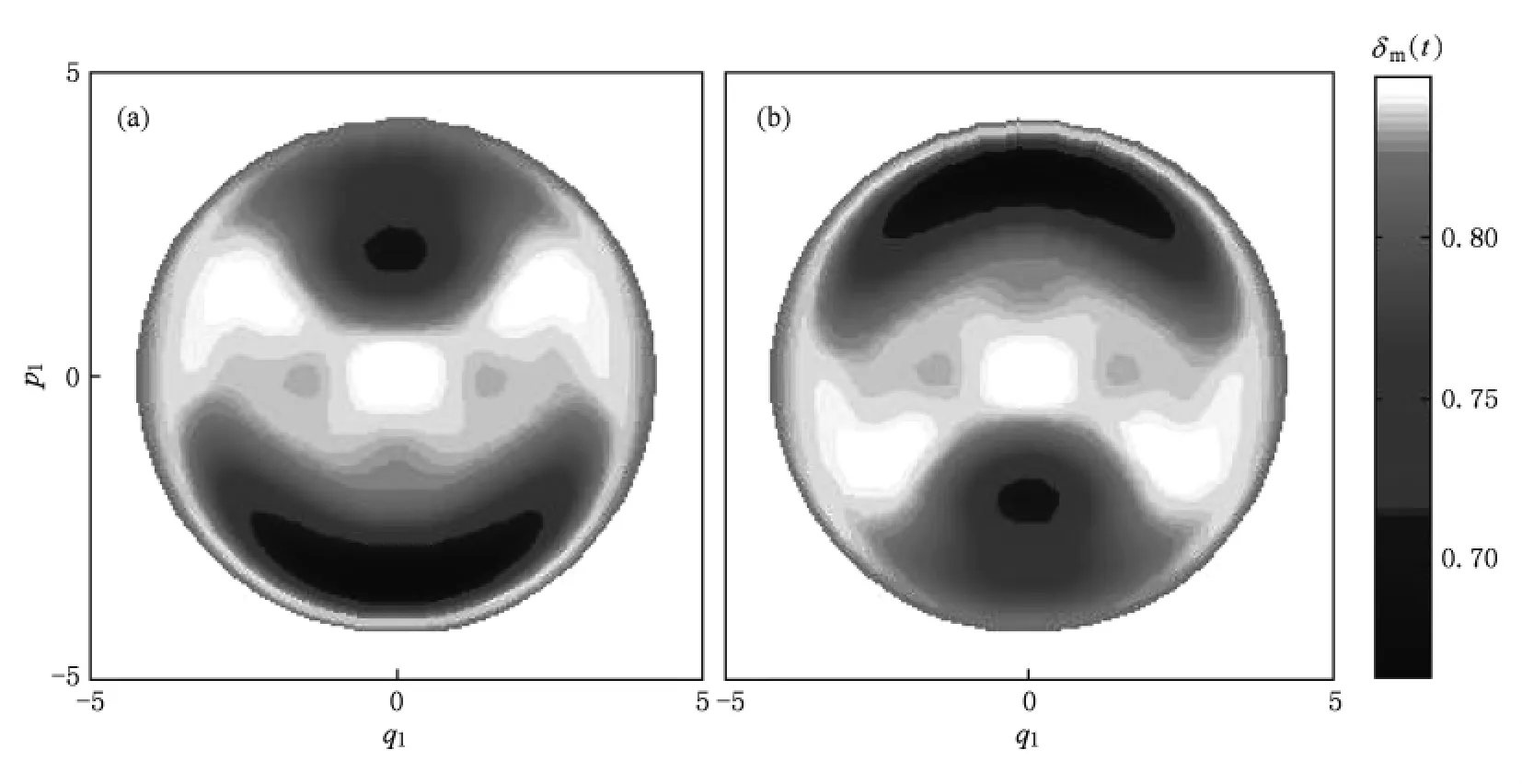
图5 取经典相空间上所有点为初态时，δm(t)随时间演化灰度图 (a)p2>0情况，(b)p2<0情况(截断时间为t =30)

为了考察Dicke模型中纠缠动力学的整体演化情况，这里将每个子庞加莱截面图(图2)上的全体点作为初态进行演化，结果也验证了上面的结论.如图5所示，时间截断为t=30，其中灰度图的值为δm(t)值.可以发现，量子相空间的δm(t)分布结构与经典相空间(图2)结构相比较非常相似，两个较大的规则区域明显，特别是经典相空间的一些小规则区域也得到了非常好的刻画，这种相似的分布结构说明系统经典动力学与量子力学纠缠动力学之间存在紧密联系，二者具有较好的对应关系.特别是，在经典相空间中除了两个大的规则区域外，在其他一些混沌区域我们很难判断系统混沌发生的强弱程度.但是δm(t)灰度图可以十分清楚地给出空间不同区域混沌的强弱程度及规则区域到混沌区域的过渡效应，从而更好地揭示相空间结构.

5.结 论

本文研究了非旋波近似条件下Dicke模型的纠缠动力学性质，在详细分析系统经典相空间结构的基础上，发现在经典庞加莱截面图上任取一点作为体系量子纠缠动力学演化的初态时，存在经典-量子“一对多”现象.我们利用统计平均的方法，通过定义平均线性熵，研究 Dicke模型经典相空间与量子动力学演化之间的关系，结果得到一种较好的量子-经典对应关系.此外，通过考察体系的整体纠缠动力学特性，发现可以更好地揭示相空间的混沌和规则结构.希望本文工作对推动腔场中量子混沌的实验实现有所裨益.

感谢浙江大学王晓光教授对本文的有益指导.

［1］Ott E 2002 Chaos in Dynamical Systems(Cambridge:Cambridge University Press)

［2］Haake F 1991 Quantum Signature of Chaos(Berlin:Springer-Verlag)

［3］Furuya K，Nemes M C，Pellegrino G Q 1998 Phys.Rev.Lett. 80 5524

［4］Wang X G，Ghose S，Sanders B C，Hu B 2004 Phys.Rev.E 70 016217

［5］Hou X W，Chen J H，Hu B 2004 Phys.Rev.A 69 042110

［6］Hou X W，Chen J H，Hu B 2005 Phys.Rev.A 71 034302

［7］Emerson J，Weinstein Y S，Lloyd S，Cory D G 2002 Phys.Rev. Lett.89 284102

［8］Weinstein Y S，Hellberg C S 2005 Phys.Rev.E 71 016209

［9］Fang Y C，Yang Z A，Yang L Y 2008 Acta Phys.Sin.57 0661 (in Chinese)［房永翠、杨志安、杨丽云 2008物理学报 57 0661］

［10］Ouyang X C，Fang M F，Kang G D，Deng X J，Huang L Y 2010 Chin.Phys.B 19 030309

［11］Zhang Y J，Xia Y J，Ren Y Q，Du X M，Liu Y L 2009 Acta Phys.Sin.58 0722(in Chinese)［张英杰、夏云杰、任延琦、杜秀梅、刘玉玲2009物理学报58 0722］

［12］Guo L，Liang X T 2009 Acta Phys.Sin.58 0050(in Chinese)［郭 亮、梁先庭2009物理学报58 0050］

［13］Lu P，Wang S J 2009 Acta Phys.Sin.58 5955(in Chinese)［卢 鹏、王顺金2009物理学报58 5955］

［14］Meng S Y，Wu W 2009 Acta Phys.Sin.58 5311(in Chinese)［孟少英、吴 炜2009物理学报58 5311］

［15］Liu J，Wang W G，Zhang C W，Niu Q，Li B W 2005 Phys. Rev.A 72 063623

［16］Liu J，Wang W G，Zhang C W，Niu Q，Li B W 2006 Phys. Lett.A 353 216

［17］Gorin T，Prosen T，Seligman T H，Znidaric M 2006 Phys.Rep. 435 33

［18］Song L J，Wang X G，Yan D，Zong Z G 2006 J.Phys.B:At. Mol.Opt.Phys.39 559

［19］Song L J，Yan D，Ma J，Wang X G 2009 Phys.Rev.E 79 046220

［20］Yan D，Song L J，Chen D W 2009 Acta Phys.Sin.58 3679(in Chinese)［严 冬、宋立军、陈殿伟2009物理学报58 3679］

［21］Chaudhury S，Smith A，Anderson B E，Ghose S，Jessen P S 2009 Nature 461 768

［22］Dicke R H 1954 Phys.Rev.93 99

［23］Zhang W M，Feng D H，Gilmore R 1990 Rev.Mod.Phys.62 867

Relations of classical-quantum correspondence in Dicke model*

Song Li-JunYan Dong1)Gai Yong-Jie1)Wang Yu-Bo2)
1)(School of Science，Changchun University，Changchun 130022，China)
2)(School of Science，Changchun University of Science and Technology，Changchun 130022，China)

22 March 2010;revised manuscript

3 May 2010)

Dicke model displays quantum chaotic dynamic properties in the non-rotating wave approximation.On the basis of properties of the classical phase space of Dicke model，we employ the one-to-many notion，namely，evolution from one point on the classical phase space to two initial coherent states.Then we obtain a good quantum phase space，which corresponds to the classical one，by using the method of averaging the statistical entangled values of two initial states in the evolution.The numerical computation shows that classical chaos can promote the origination of bipartite entanglement，and simultaneously，the average entanglement can be regarded as the signature of quantum chaos.A good classica-quantum correspondence can be obtained by using the average entanglement.

Dicke model，non rotating wave approximation，quantum chaos，classical-quantum correspondence

*国家自然科学基金(批准号:10947019)、吉林省自然科学基金(批准号:20101514)和吉林省教育厅科技研究基金(批准号:2009237)资助的课题.

PACS:03.65.Ud，03.67.Hk，05.45.Mt，42.50.Dv

*Project supported by the National Natural Science Foundation of China(Grant No.10947019)，the Natural Science Foundation of Jilin Province of China(Grant No.20101514)and the Science and Technology Research Program of the Education Bureau of Jilin Province，China(Grant No. 2009237).