失谐驻波管及其极高纯净驻波场性质的研究*

闵 琦 刘 克

1)(中国科学院声学研究所噪声与振动重点实验室，北京 100190)

2)(红河学院，蒙自 661100)

(2010年1月12日收到;2010年5月16日收到修改稿)

失谐驻波管及其极高纯净驻波场性质的研究*

闵 琦1)2)†刘 克1)

1)(中国科学院声学研究所噪声与振动重点实验室，北京 100190)

2)(红河学院，蒙自 661100)

(2010年1月12日收到;2010年5月16日收到修改稿)

由直径不同的两级直圆管连接而成的两级突变截面驻波管具有失谐性，即高阶共振频率不是一阶共振频率的整数倍.两级突变截面驻波管的失谐性质能够很好地抑制一阶共振频率激励下的大振幅非线性驻波畸变产生的高次谐波，从而获得大振幅纯净驻波场.通过对两级突变截面驻波管失谐性质的研究，采用大功率扬声器正接等措施，利用两级突变截面驻波管的失谐性质在一阶共振频率激励下获得了184 dB的极高纯净驻波场，并对二至五阶共振频率激励下的声场进行了相应的实验研究.在二阶、四阶共振频率激励下分别获得了180和166 dB波形比较规整的大振幅非线性驻波，并在三阶、五阶共振频率激励下观察到了谐波饱和现象和锯齿波.

失谐驻波管，大振幅驻波，畸变，饱和

PACS:43.10.Ln，43.25.Cb，43.25.Gf

1.引 言

大振幅非畸变纯净驻波场可用于传声器的校准、化学反应过程的控制等［1，2］，尤其是近年来，为提高热声机的功率和效率，大振幅非畸变纯净驻波场的研究和获取更受到人们的关注［3—9］.然而，大振幅驻波由于非线性效应会产生高次谐波，能量由基波向高次谐波转移，从而使波形发生畸变.当大振幅驻波场声压级提高到一定程度时，高次谐波将趋于饱和，最终导致激波的出现.激波的出现极大地消耗了大振幅驻波场的能量，致使大振幅驻波场声压级将无法再进一步得到提高［1，10］.

围绕着大振幅驻波场高次谐波的抑制和大振幅纯净驻波场的获取到目前为止主要有三种方法:一是主动控制法，即在驻波管内针对大振幅驻波场的高次谐波尤其是二次谐波人为地引入次级声场，当次级声场的幅值和相位与大振幅驻波场的高次谐波幅值和相位满足一定关系时，高次谐波将被部分甚至完全地抑制［11，12］;二是人为地将色散效应引入驻波管，如在驻波管两侧安装亥姆霍兹共振器，使得驻波管具有失谐性，即高阶共振频率不是一阶共振频率的整数倍，基波能在驻波管内共振而高次谐波却不能，从而有效地抑制高次谐波能量的聚集和增加［13，14］;三是采用非等截面驻波管，不同于等截面驻波管，非等截面驻波管本身就具有失谐性，可利用其自身的失谐性质来有效地抑制高次谐波，这样的驻波管称之为失谐驻波管.截面连续变化失谐驻波管通过沿轴向做整体振动以获取大振幅纯净驻波场的技术被称为共振强声合成［1，15—18］.

两级突变截面驻波管属于失谐驻波管，本身具有很好的失谐性.以扬声器为驱动声源的两级突变截面驻波管曾经有过相关的研究，但获得的纯净驻波场声压级均未超过174 dB，并且对其声学性质尤其是管内大振幅驻波场谐波饱和特性的研究仍未见详细的报道［2］.为此，我们曾采用大功率扬声器侧接以模拟活塞声源的办法在一阶共振频率下获得了180 dB的纯净驻波场，并对一至三阶共振频率激励下的谐波饱和情况进行了相应的实验研究［19］.与此不同，本文采用大功率扬声器正接的方法，利用两级突变截面驻波管的失谐性质在一阶共振频率激励下获得了184 dB的大振幅非畸变极高纯净驻波场.在此基础上，对一阶共振频率激励下的波形畸变和谐波饱和情况进行了实验研究，直到声压级达到184 dB时仍未观察到谐波饱和现象.在随后的对二至五阶共振频率激励下的声场进行的相应实验研究中，观察到了在极高声压情形下的一些实验规律.在二阶、四阶共振频率激励下最高声压级分别达到180和166 dB时，波形有一定畸变，但谐波仍未出现饱和迹象;而在三阶、五阶共振频率激励下，当声压级分别达到166和154 dB时，观察到了谐波饱和现象和波形畸变成为锯齿波.

2.相关理论

两级突变截面驻波管由直径不同的两段直圆管粗管A，细管B连接而成，连接处管径从粗管直接过渡到细管;除连接端外，粗管A另一端安放声源，细管B另一端则刚性封闭.具体情况如图1所示.管A，管 B的长度、直径和截面积分别为 lA，dA，sA和lB，dB，sB.定义管长比 l=lA/lB，截面积比 s=sA/sB以及总管长L=lA+lB.

管内是空气，在扬声器驱动下，如果两级突变截面驻波管安放声源和封闭端的声压分别为 pA，pB，可定义驻波管两端面声压级传递函数为［19］

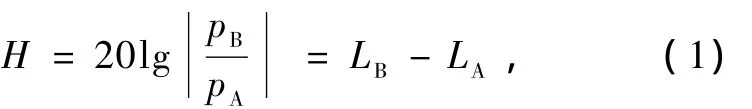
其中LA，LB分别是两级突变截面驻波管相应端面的声压级.

由传递矩阵法可以得到联系两级突变截面驻波管两端面声压和质点速度的传递矩阵公式［20］

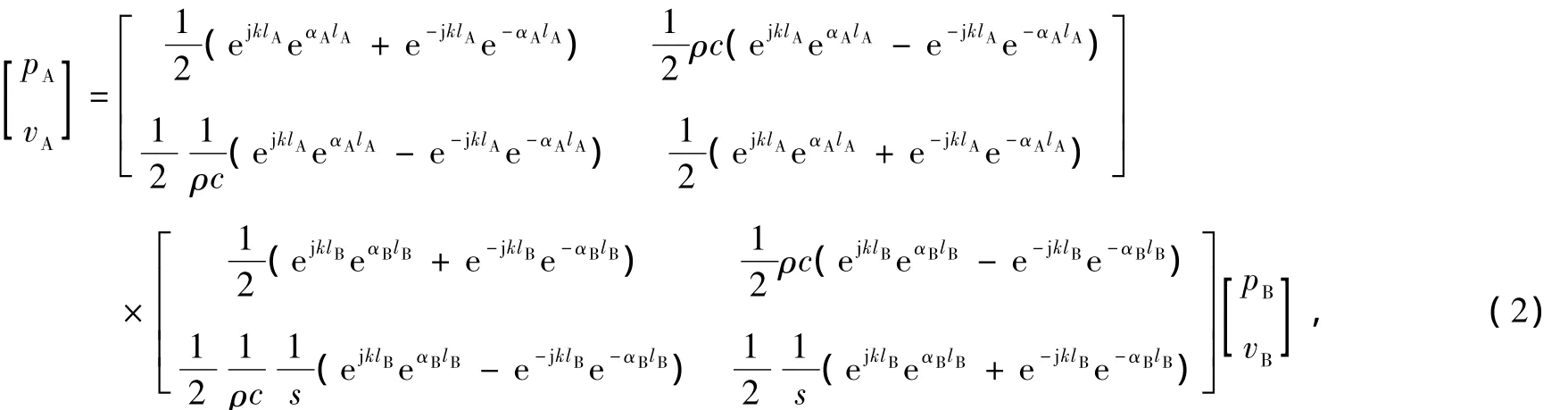
其中k为波数，vA，vB为两端面的质点速度，这里vB分别为平面波在管A，B内传播的衰减系数，单位为mm－1.与模态分析法相比，当突变截面驻波管的级数进一步增加时，传递矩阵法相对简便的优势会逐渐显现出来［21］.

由传递矩阵(2)式可以得到不考虑耗散情况下的两级突变截面驻波管的共振条件为［2］

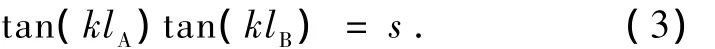
图2根据(3)式绘出了两级突变截面驻波管共振条件图，横、纵坐标轴分别为 lB/λ，lA/λ，λ 为波长.图中实线是s分别取1和9.8时根据(3)式所绘出的，其中9.8是后面实验系统所用驻波管的截面积比.图中还做出了通过原点标记为“l=1”的虚直线，其斜率为1.当l=1时，不同s下的共振就发生在这一虚直线与相应实线的交点处.共振阶数由交点离原点的相对距离决定，离原点最近的为一阶，之后依次为二阶、三阶等高阶.l取其他常数时，不同s下的共振由通过原点斜率取l的虚直线与相应的实线交点确定.为显示两级突变截面驻波管的失谐性质，我们选择了l=1，s=9.8的情形.此时满足一至三阶共振条件的交点P1，P2和 P3分别在图上进行了标记，对应的横、纵坐标的数值分别标注在相应括号内.从括号内的数值可以看出P1，P2和P3对应的横坐标不成整数倍，而横坐标 xn=lB/λn=(lB/c)fn，n=1，2，3，…为共振阶数，λn，fn分别为n阶共振时的波长和频率，c为声速，由此可以清楚地看出这一情形下两级突变截面驻波管的失谐性质.其他情形下的失谐性质可以通过类似的讨论得到说明.

由图2还可看出，可以根据实线曲率的正负将

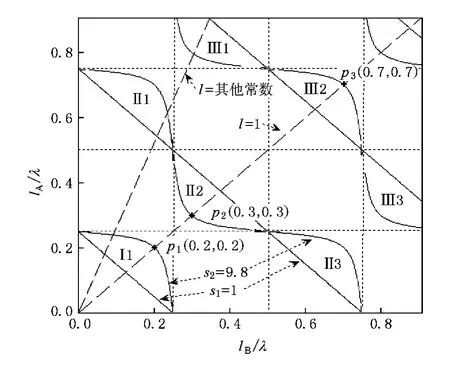
图2中实线所在区域划分为两类区域，即曲率为正的区域，如一阶共振区域Ⅰ1，二阶共振区域Ⅱ1及Ⅱ3等，以及曲率为负的区域，如二阶共振区域Ⅱ2，三阶共振区域Ⅲ1和Ⅲ3等.当s=1时，两类区域内的共振满足总管长 L=(2n－1)λ/4;而对于 s≠1，两类区域有所不同，曲率为正的区域共振时 L>(2n－1)λ/4，并且 s越大，L越大于(2n－1)λ/4，曲率为负的区域情况恰恰相反.

3.实验系统

材质的粗管 A，细管 B通过不锈钢转接环 B相连接，左端面与不锈钢转接环A连接，右端面由不锈钢封盖B密封，转接环和封盖壁厚均超过10 mm.管A，B的长度、内径及壁厚分别是 1217，25和10 mm 以及 981，8和 7 mm;l为 1.24，s为 9.8.

信号驱动部分:扬声器通过铝合金材质的刚性锥形转接环与驻波管左端的转接环A正接;扬声器采用大功率 McCauley2010，其最大输出功率为350 W，频率范围为0.04—2.5 kHz，口径和线圈电阻分别为10 in(1 in=25.4 mm)和8 Ω.功放和激励信号源分别采用美国 DSA1850B(CAC)和丹麦 BK Pulse3560C.

信号采集处理部分:左右端面处的传声器A和B分别安放于转接环A侧壁和封盖B中央直径为7 mm的小孔内;声压级低于169 dB时，左、右端面处的传声器 A，B均采用 BK4944驻极体式传声器，当右端面声压级超过169 dB时，右端面处的传声器更换为BK4941电容式传声器.测试前，采用BK4228型活塞式校准仪对传声器进行校准，采集到的声压信号由 BK Pulse3560C进行实时处理.

与文献［19］一样，实验在室温和大气压下进行，PC机通过网络接口与实验系统相连接并对实验全程进行实时监控.

实验系统如图1所示，主要由三部分组成，即失谐驻波管部分，信号驱动部分，信号采集处理部分.这里的失谐驻波管部分和信号采集处理部分与文献［19］中的实验系统基本一致，不同之处来自于信号驱动部分中的扬声器及其连接方式.

失谐驻波管部分:即突变截面驻波管，不锈钢

4.实验结果

4.1.声压级传递函数

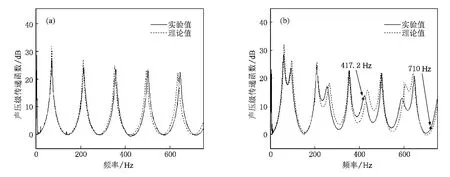
图3 驻波管声压级传递函数图 (a)管A等截面驻波管声压级传递函数，(b)两级突变截面驻波管声压级传递函数

图3(a)，(b)分别给出了仅由管A构成的等截面驻波管以及由管A，B组成的突变截面驻波管的声压级传递函数在频域上的分布，其中理论值由传递矩阵公式(2)数值计算得到，实验值采用稳态白噪声信号激励实验测量得到，传递函数峰值处即是共振频率所在的位置.由图3可以看出，仅由管A构成的等截面驻波管共振频率均匀分布在频域上，实验值和理论值符合得很好，而由管A，B组成的突变截面驻波管共振频率在频域上的分布并不均匀，由此可以看出两级突变截面驻波管的失谐性质.

对于突变截面驻波管，1，3，5等奇数阶共振频率实验值和理论值符合得很好，差异主要出现在2，4，6等偶数阶共振频率上，实验值小于理论值，并且阶数越高两者差距越大.与管A等截面驻波管相比，两级突变截面驻波管传递函数理论值和实验值在偶数阶共振频率处差别较大的原因是因为管B的引入造成的，管B的直径仅为8 mm，管壁边界层对声场产生了一定的影响.图3(b)还分别标出了三阶、五阶共振频率的倍频417.2和710 Hz的位置，在后面的讨论中将会看到它们位置的特殊性与三阶、五阶共振频率下的波形畸变有着很大的关系.

4.2.一阶共振频率下的极高纯净驻波场及其谐波特性

图4给出了在一阶共振频率激励下管A等截面驻波管和两级突变截面驻波管右端面声压级各自随驱动电压的增加情况，其中管A等截面驻波管一阶共振频率为71 Hz，而两级突变截面驻波管一阶共振频率为60.1 Hz.对比图中两条曲线后可以发现，两种驻波管的声压级各自随驱动电压增加的幅度基本相同，但在相同的驱动电压下，两级突变截面驻波管右端面声压级均比管A等截面驻波管右端面声压级高出4 dB以上.

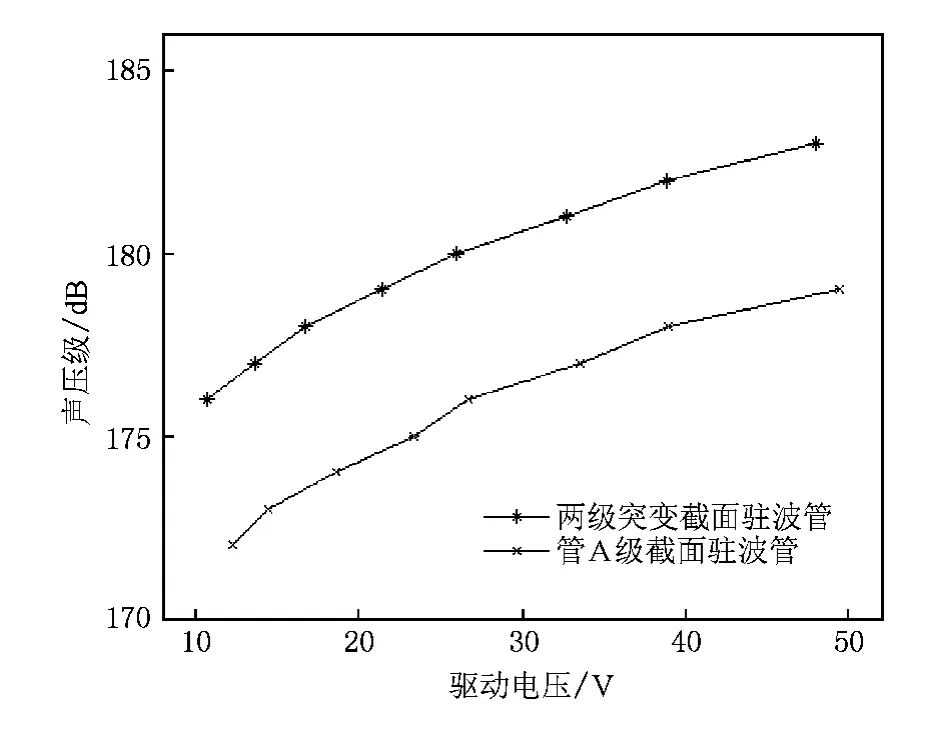
图5(a)，(b)分别给出了一阶共振频率71 Hz激励下管A等截面驻波管右端面高次谐波随基波的增长情况以及179 dB时的时域波形.由图5(a)可以看出，随着基波声压级的提高，二次谐波增长较慢，而三次谐波增长明显，这是由于三次谐波频率与二阶共振频率相等.起初基波声压级为172 dB时，二次、三次谐波声压级分别为133和128 dB，与基波相比分别相差39和44 dB.当基波声压级提高到179 dB时，三次谐波高过了二次谐波，二次谐波声压级增加到142 dB，与基波相差37 dB，而三次谐波增加到151 dB，与基波的差距由起初的44 dB减小到28 dB.此时，二次、三次谐波能量分别是基波能量的0.02%和0.16%，波形畸变为5.39%.由图5(b)时域波形可以看出179 dB时的波形仍是比较规则的正弦波波形.

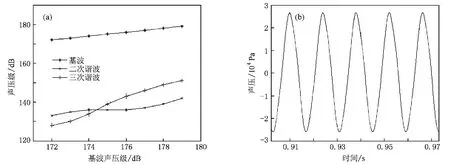
图3(b)表明一阶共振频率激励下两级突变截面驻波管声压级传递函数值最大，而实验在一阶共振频率激励下在两级突变截面驻波管右端面获得了最高184 dB的极高声场.图6(a)，(b)所示分别为一阶共振频率60.1 Hz激励下，两级突变截面驻波管右端面声压级达到184 dB时两端面测得的频谱.从图6(a)，(b)可以看出，左、右端面处的高次谐波声压级依次减小.此时，左端面基波声压级为160 dB，二次、三次谐波声压级分别为 147和142 dB，与基波相差13和18 dB，二次和三次谐波能量分别是基波的5.01%和1.58%，波形畸变达到34.98%;对于右端面，基波声压级虽然已经达到184 dB，二次、三次谐波声压级分别为 165和 152 dB，与基波相比相差19和32 dB，二次和三次谐波的能量却只是基波能量的1.26%和0.06%，波形畸变仅为13.7%.

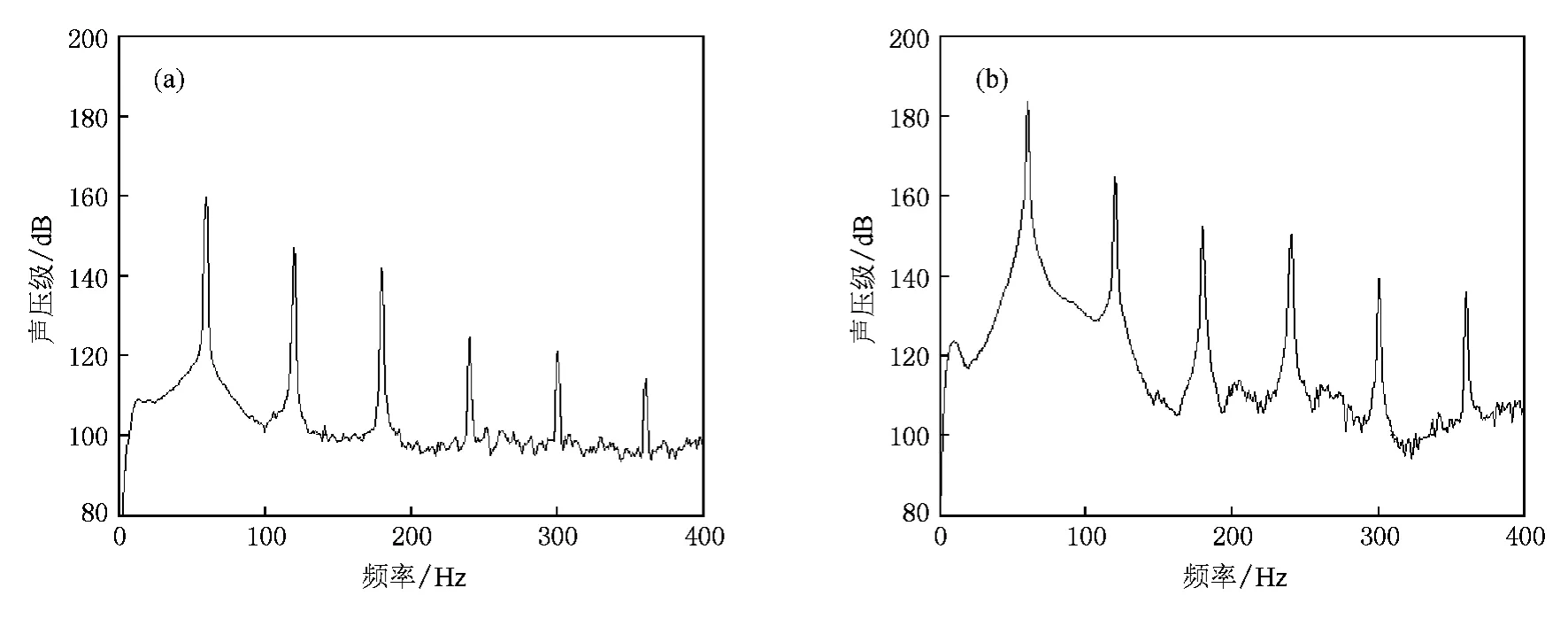
图7(a)，(b)分别给出了一阶共振频率激励下两级突变截面驻波管右端面声压级达到184 dB时两端面测得的时域波形.从图7(a)，(b)可以看出，尽管左端面的声波波形畸变已很厉害，右端面的声压级已经达到184 dB的极高声压级，但右端面的声波波形仍保持比较规整的正弦波波形.此时，相对于静态气压，右端面声波波形整体向下平移了8 kPa，声压幅值的绝对值最大达到47.9 kPa，接近静态标准大气压的二分之一，由此计算出的质点速度最大峰值为119.8 m/s，超过了声速的三分之一，管内声场已处于极端非线性.

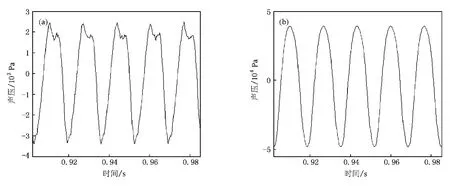
图8(a)，(b)分别给出了一阶共振频率60.1 Hz激励下两级突变截面驻波管右端面谐波和两端面基波增长情况.由图8(a)可以看出，与管A等截面驻波管一样，随着基波声压级的增加，右端面二次、三次谐波的声压级也随之增加，但与管A等截面驻波管不同的是，二次谐波的增长几乎与基波平行，三次谐波开始增长较快，但随后变缓.直到基波达到184 dB时，二次、三次谐波都没有表现出饱和迹象.图8(b)显示，两端面基波声压级同步增加，两端面基波声压级在最初的176 dB时相差最大，为31 dB，随着右端面基波声压级的增加，差距逐渐减小，到184 dB时差距减小到24 dB.为做对比，图8(b)还标示出了由图3(b)所示一阶共振频率下声压级传递函数理论值和实验值分别估计出的左端面声压级.

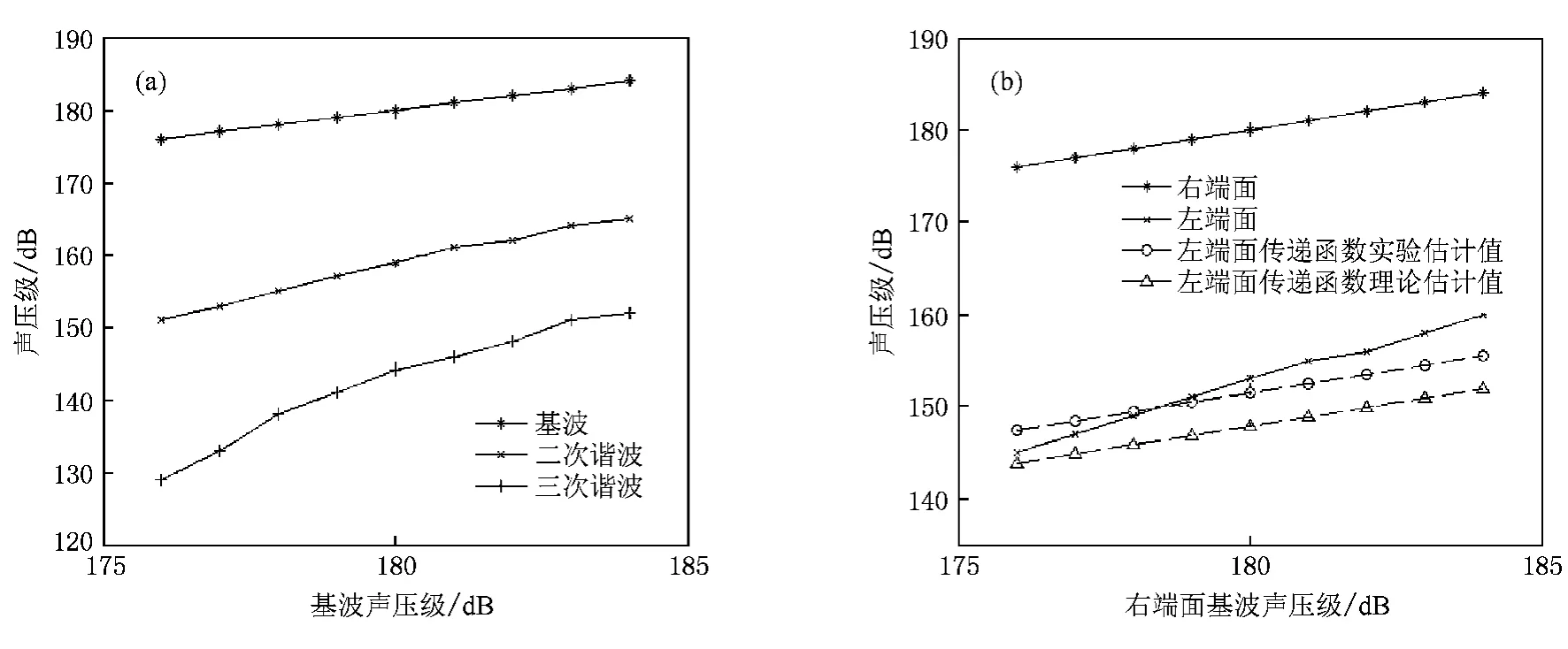
图8 一阶共振频率60.1 Hz激励下两级突变截面驻波管右端面谐波和两端面基波增长情况 (a)一阶共振频率下两级突变截面驻波管右端面谐波，(b)一阶共振频率下两级突变截面驻波管两端面基波

4.3.高阶共振频率下的驻波场及其谐波特性

图9分别给出了二至五阶共振频率激励下的高次谐波增长情况，其中，二至五阶共振频率如图3(b)所示，依次分别为 92.3，208.6，254.6和 355 Hz.由图9可以看出，随着基波声压级的提高，二至五阶共振频率激励下的高次谐波声压级也都随之增加，但增长的情况各不相同.比较而言，可把高次谐波增长情况分为两类:一是二阶和四阶共振频率激励下高次谐波的增长，高次谐波均未出现饱和现象;二是三阶和五阶共振频率激励下的高次谐波的增长，高次谐波都出现了饱和现象.对于二阶和四阶共振频率，当声压级分别达到180和166 dB时，从图9(a)，(c)可以看出，二阶共振频率下的二次、三次谐波声压级分别为161和154 dB，分别是基波能量的1.26%和0.25%;而四阶共振频率下的二次、三次谐波分别为135和131 dB，分别是基波能量的0.08%和0.03%.

就三阶和五阶共振频率而言，由图9(b)，(d)可以看出，当基波声压级增加时，高次谐波跟着快速增加.在三阶共振频率激励下，起初基波声压级为158 dB时，二次、三次谐波声压级分别是142和124 dB，分别是基波能量的2.51%和0.04%;而当基波声压级增加到166 dB时，二次、三次谐波声压级也随之增加到158和148 dB，其能量与基波能量相比分别增加到15.8%和1.58%.对于五阶共振频率，开始基波声压级为145 dB时，二次、三次谐波声压级分别为128和95.6 dB，是基波能量的2.0%和0.001%;当基波声压级增加到154 dB时，二次、三次谐波声压级分别为147和119 dB，达到基波能量的20%和0.03%.

图10给出了二至五阶共振频率激励下声压级分别达到180，166，166和154 dB时的时域波形.对于未出现饱和现象的二阶共振频率，从图10(a)可以看出，二阶共振频率下的时域波形出现了一定的畸变.与一阶共振频率下184 dB时的声场对比后可以发现，两者二次谐波能量均为基波能量的11.2%，但三次谐波能量在一阶共振频率下为基波能量的0.06%，而在二阶共振频率下增加到0.25%，由于这一差异，波形畸变从一阶共振频率时的13.7%增加到了现在的16.2%.由时域波形图7(b)和10(a)对比可以直观地看出波形畸变程度的不同.对于同样未出现饱和现象的四阶共振频率，从图10(c)可以看出，时域波形仍是比较规整的正弦波波形，畸变仅为4.6%.

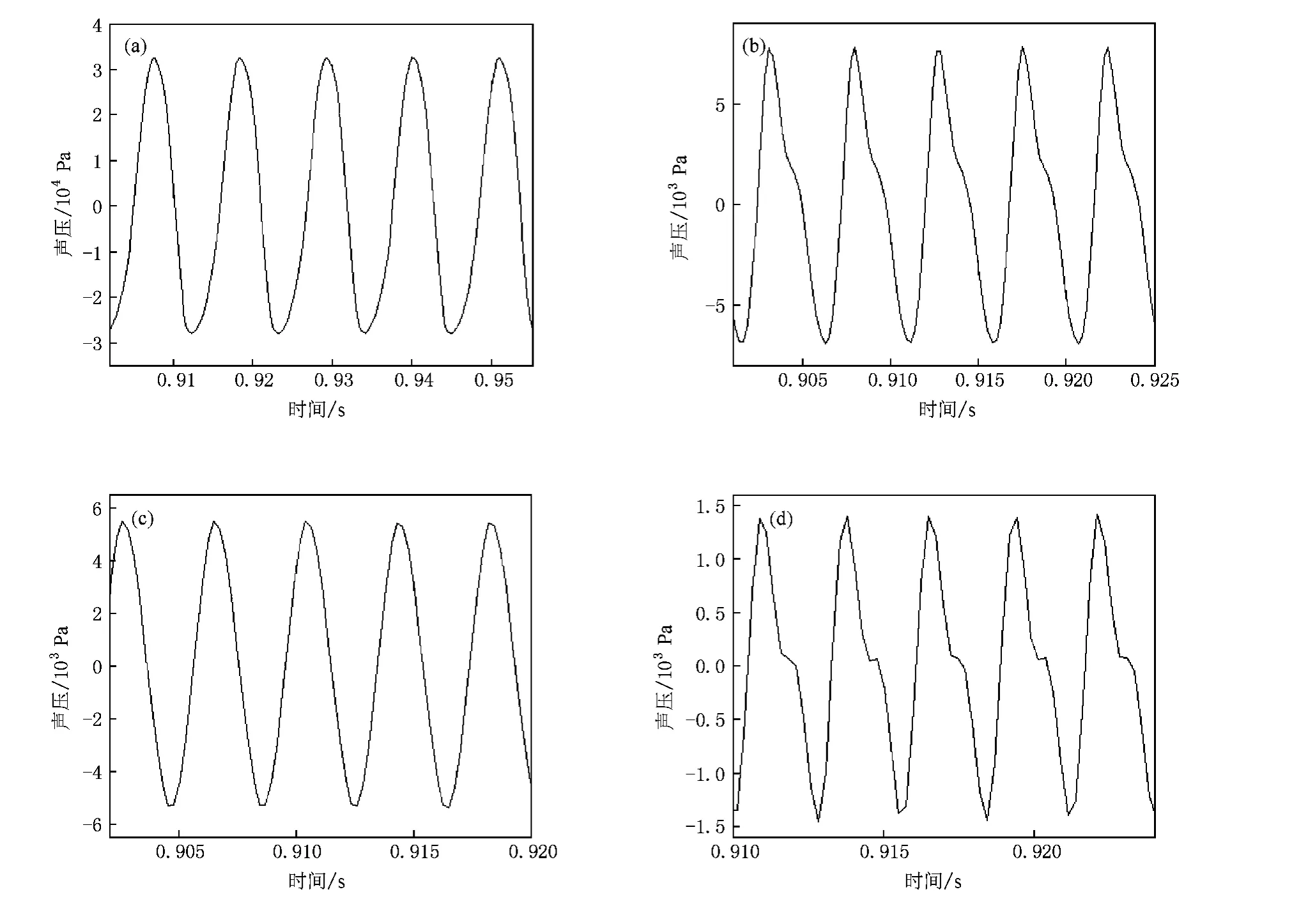
图10 高阶共振频率下两级突变截面驻波管右端面声波时域波形 (a)二阶180 dB，(b)三阶166 dB，(c)四阶166 dB，(d)五阶154 dB

对于出现饱和现象的三阶和五阶共振频率，当基波声压级分别达到166，154 dB时，波形畸变已经分别达到52.4%和46.5%.从图10(b)，(d)可以清楚地看出，此时时域波形畸变成了类似于单级驻波管内的大振幅驻波畸变后得到的锯齿波［1，22］.从图3(b)标出的三阶、五阶共振频率的倍频即各自二次谐波频率417.2和710 Hz的位置可以看出，它们分别接近六阶共振频率实验值422.5 Hz和声压级传递函数实验值谷值频率699.6 Hz.三阶共振频率倍频处的声压级传递函数实验值是12.7 dB，六阶共振频率处的是13.8 dB，两者很接近;而五阶共振频率倍频处声压级传递函数实验值是0.84 dB，谷值处的是0.39 dB，两者同样也很接近.

5.结 论

与等截面驻波相比，两级突变截面驻波管具有良好的失谐性，可以获得声压级更高的大振幅纯净驻波场.利用两级突变截面驻波管的失谐性质，在一阶共振频率激励下可以获得184 dB的极高纯净驻波场，并在二阶、四阶共振频率激励下分别可以获得180和166 dB的大振幅纯净驻波场.

对于两级突变截面驻波管，当三阶、五阶共振频率的倍频即二次谐波频率分别接近六阶共振频率和声压级传递函数的谷值频率时，三阶、五阶共振频率激励下的大振幅驻波同样会出现类似于单级驻波管内大振幅非线性驻波表现出的波形畸变和谐波饱和现象;并在三阶、五阶共振频率激励下，当驻波场声压级分别达到166和154 dB时观察到了锯齿波.

［1］Lawrenson C C，Lipkens B，Lucas T S，Perkins D K，van Doren T W 1998J.Acoust.Soc.Am.104 623

［2］BeranekL L 1998AcousticalMeasurements(New York:American Institute of Physics)p374

［3］Back S，Swift G W 1999Nature399 335

［4］Swift G W 1988J.Acoust.Soc.Am.84 1145

［5］Penelet G，Gusev V，Lotton P，Bruneau M 2005Phys.Rev.E 72 016625

［6］Biwa T，Tashiro Y，Mizutani U，Kozuka M，Yazaki T 2004Phys.Rev.E 69 066304

［7］Smith E 1998Phys.Rev.E 58 2818

［8］Yazaki T，Iwata A，Maekawa T，Tominaga A 1998Phys.Rev.Lett.31 3128

［9］Gusev V E，Bailliet H，Lotton P，Job S，Bruneau M 1998J.Acoust.Soc.Am.103 3717

［10］Ma D Y 1996Acta Phys.Sin.45 796(in Chinese)［马大猷1996物理学报45 796］

［11］Huang P T，Brisson J G 1997J.Acoust.Soc.Am.102 3256

［12］Huang X Y，Nguyen N T，Jiao Z J 2007J.Acoust.Soc.Am.122 38

［13］Sugimoto N，Masuda M，Hashiguchi T，Doi T 2001J.Acoust.Soc.Am.110 2264

［14］Sugimoto N，Masuda M，Hashiguchi T 2003J.Acoust.Soc.Am.114 1772

［15］Ilinskii Y A， Lipkens B，Lucas T S， vanDorenT W，Zabolotskaya E A 1998J.Acoust.Soc.Am.104 2664

［16］Hamilton M F，Ilinskii Y A，Zabolotskaya E A 2009J.Acoust.Soc.Am.125 1310

［17］Chun Y D，Kim Y H 2000J.Acoust.Soc.Am.108 2765

［18］Li X，Finkbeiner J，Raman G，Daniels C，Steinetz B M 2004J.Acoust.Soc.Am.116 2814

［19］Min Q，Peng F，Yin Y，Liu K 2010Acta Acustica35 185(in Chinese)［闵 琦、彭 锋、尹 铫、刘 克2010声学学报35 185］

［20］Munjal M L 1987Acoustics of Ducts and Mufflers with Application to Exhaust and Ventilation System Design(New York:Wiley)p75

［21］Gibiat V，Barjau A，Castor K，Chazaud E B 2003Phys.Rev.E 67 066609

［22］Maa D Y，Liu k 1995J.Acoust.Soc.Am.98 2753

PACS:43.10.Ln，43.25.Cb，43.25.Gf

Dissonant standing-wave tube and the extremely nonlinear pure standing wave field*

Min Qi1)2)†Liu Ke1)
1)(Key Laboratory of Noise and Vibration Research，Institute of Acoustics，Chinese Academy of Sciences，Beijing 100190，China)
2)(Honghe University，Mengzi661100，China)
(Received 12 January 2010;revised manuscript received 16 May 2010)

A standing-wave tube consisting of two tubes with abrupt changing diameters is dissonant，that is，its higher resonance frequencies are not integral multiples of the fundamental one.Using the dissonant property of the said standingwave tube，the harmonics can be well suppressed and extremely pure nonlinear standing wave can be obtained at the first resonance frequency.Based on the study of the dissonant property of this standing-wave tube and by the straight connection of a high-power loudspeaker，184 dB extremely pure nonlinear standing-wave field was obtained at the first resonance frequency.Moreover，the nonlinear standing-wave fields were experimentally investigated separately for the second resonance frequency up to the fifth.Relatively regular nonlinear standing-wave field of 180 dB was obtained at the third resonance frequency，and that of 166 dB was obtained at the fourth resonance frequency.The harmonics saturation phenomena and zigzag waveforms were observed at the third and the fifth resonance frequency，respectively.

dissonant resonator，large-amplitude standing wave，distortion，saturation

*国家自然科学基金(批准号:10574135)和中国科学院三期知识创新工程重要方向(批准号:KJCX2-YW-W02)资助的课题.

*Project supported by the National Natural Science Foundation of China(Grant No.10574135)and the Main Direction Program of Knowledge Innovation of Chinese Academy of Sciences(Grant No.KJCX2-YW-W02).