基于非连续能量耗散的滑动摩擦系数计算模型*

龚中良 黄 平

1)(中南林业科技大学机电工程学院，长沙 410004)

2)(华南理工大学机械与汽车工程学院，广州 510640)

(2010年3月16日收到;2010年5月23日收到修改稿)

基于非连续能量耗散的滑动摩擦系数计算模型*

龚中良1)†黄 平2)

1)(中南林业科技大学机电工程学院，长沙 410004)

2)(华南理工大学机械与汽车工程学院，广州 510640)

(2010年3月16日收到;2010年5月23日收到修改稿)

分析了界面摩擦状态下能量非连续耗散过程，建立了简化条件下晶体材料界面摩擦滑动摩擦系数计算模型.结果表明:在弹性接触状态下，滑动摩擦系数与载荷及实际接触面积无关，当实际接触面积接近名义接触面积时，滑动摩擦系数随载荷增加而减小.在缓慢滑动时，滑动摩擦系数随滑动速度的增高而缓慢增大，相对滑动速度愈高，滑动摩擦系数增大趋势愈显著.滑动摩擦系数随晶格常数的增加而降低，而当晶格常数较大时，其变化对滑动摩擦系数影响较小.同时，滑动摩擦系数随原子的可能温升增加而增大.研究结论对工程应用及相关的理论研究具有一定的参考意义.

滑动摩擦系数，非连续能量耗散，界面摩擦

PACS:46.55.+d，81.40.Pq

1.引 言

从摩擦的成因来看，热效应和动力学特性是导致摩擦产生和能量消耗的最主要的两个因素.当两表面做相对运动时，引起运动的力就做功，因此在接触表面上有能量损耗.研究发现，摩擦所做的功除部分转化为表面能、声能和光能等外，85%—95%转化为热能［1］.因此，摩擦功的热耗散可间接反映摩擦副的摩擦状态.

滑动摩擦系数是反映摩擦状态的主要物理参数之一.从微观上看，界面摩擦时影响摩擦状态的主要因素为材料的微观结构、表面能、表面形貌、相对滑动速度及温度等［2］.由于固体摩擦机理仍未清楚，现有的摩擦理论只能解释而不能预测结果［3—6］.因此在实际应用中，往往通过实验获得各种材料的摩擦系数.近年来，随着对摩擦机理研究的进一步深入［7］，尤其是纳米摩擦学的发展，人们试图从摩擦成因上来研究摩擦系数的计算模型，并探讨各主要因素对摩擦系数的影响规律［8—10］.以往的研究均建立于经典理论基础上，且在研究时将摩擦过程中原子获得或耗散的能量认为是连续的［11—13］.然而，以α-Fe为例，其晶格类型为体心立方晶格，晶格常数a=2.87×10－10m，当摩擦副下表面与上表面间以相对速度为v=0.001 m/s缓慢滑动时，其表面原子在界面周期势能场作用下的受迫振动频率fforced=3.49 MHz.显然，该频率接近紫外频率，适应量子理论研究范畴.作者［14］曾基于微观粒子能态分立——即原子只有在周围辐射场的能量达到基本能量子的整数倍时原子才能吸收或释放能量的观点，建立了界面摩擦过程中微观能量耗散的量子力学模型，并通过对所建立模型的定量分析，得出了界面摩擦过程中摩擦能量非连续耗散的结论.丁凌云等［15］基于声子摩擦能量耗散，提出当局部的热平衡态破坏时，振子将振荡激发声子并耗散能量，从而使非热平衡状态向热平衡态发展.因此，研究摩擦过程中的能量耗散，必须考虑原子能态的非连续性.

本文以晶体材料界面摩擦过程为背景，结合摩擦功全部耗散为系统热能的观点，建立了基于能量非连续耗散的滑动摩擦系数计算模型，探讨了相对滑动速度、接触面积、摩擦界面法向正应力、晶格常数、原子温升等内外因素对滑动摩擦系数的影响规律.为简化分析，在模型建立过程中，一方面只考虑摩擦界面原子在周期势场作用下因受迫振动导致的能态变化，忽略相邻原子之间相互作用及原子的自激振荡对能量耗散的影响;另一方面，不考虑摩擦系统的边界条件，并假设摩擦系统为理想绝热系统.因此，本研究只是一种理论研究方法上的探讨，其结论有待进一步验证.

2.原子能量非连续吸收与释放

在量子力学理论中［16］，Wien提出辐射能量分布定律

其中υ为频率，c为光速，T为温度，α和β为常数.

(1)式只在波长较短、温度较低时才与实验结果相符合，而在长波区域则普遍低于实验值.1899年普朗克提出了在达到平衡时辐射场的能量密度ρ(υ)与振子平均能量的关系式

通过比较(1)式与(2)式，并考虑到低频区的实验结果，采用内差法得出辐射的能量密度为

其中γ为常量.

将(3)式与(2)式比较，得振子的平均能量为

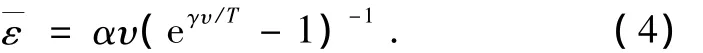
由此，普朗克提出了能量量子化假设:1)黑体的腔壁是由无数个带电的谐振子组成的，这些谐振子不断吸收和辐射电磁波，与腔内的辐射场交换能量;2)这些谐振子所具有的能量是分立的，它的能量与其振动频率υ成正比，即

其中h为普朗克常量.

由于振子与辐射场交换的能量ε是一个离散的变量，只能取基本单元能量子ε0的整数倍，即

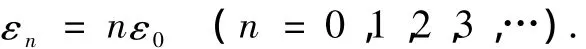
利用统计理论求得在周围场辐射条件下原子交换能量的平均值

其中υ为引起原子能量交换的周围辐射场频率，本文为摩擦界面原子在周期性界面势能场作用下原子受迫振动的频率，k为 Boltzmann常量，T为原子交换能量后的温度变化.

对比(4)式和(5)式，可得到 α和 γ两常数分别为

1913年玻尔将光的量子理论引入到原子结构理论中来，提出了定态假说和频率假说:在原子系统中存在一系列的定态，电子在这些定态的能量取离散值，原子在定态中不发射也不吸收电磁辐射能，原子在两个定态能级En>Em跃迁时，发射或吸收的电磁辐射的频率υ满足hυ=En－Em.原子系统的每个变化只能从一个定态完全跃迁到另一个定态，这种跃迁可以是自发从高能态跃迁到低能态，也可以在外界的干扰下从低能态跃迁到高能态.

显然，在界面摩擦时，界面势能场的周期变化及界面原子平衡态失稳等因素都将对原子的能态产生影响.由于界面原子吸收与释放能量的能力是非连续的，因此在界面摩擦过程中，当界面势能场对原子的激励未达到原子能态变化所需能量时，就没有摩擦功的耗散，只有当界面激励能量达到基本能量子的整数倍时，才可能出现摩擦功的突然耗散.

3.滑动摩擦系数计算模型

为简化计算，假设材料表面晶胞中只有最表面原子参与接触，则根据不同的晶格类型可以计算出最表面每个原子所占面积s0与晶格常数a的关系为:对于体心立方晶胞，如 α-Fe，β-Ti，W，V，Cr等，s0=a2;对于面心立方晶胞，如 γ-Fe，Al，Cu，Ni，Au 等，s0=0.5a2;对于密排六方晶胞，如 α-Ti，Be，Zn，Mg等，s0=1.3a2.

以体心立方晶胞类型材料为例，当摩擦副为同种晶体材料时，在任一时刻摩擦界面某一面上实际接触的原子数(在不考虑接触边缘的情况下)为

其中S为实际接触面积.

假设摩擦副一界面静止，另一界面在Δt时间内以速度v从位置A滑动至位置B，如图1所示.

如果滑动过程中摩擦界面的实际接触面积不变，则在 Δt时间内，S区域中任一原子受界面周期势能场变化而被激励的次数为

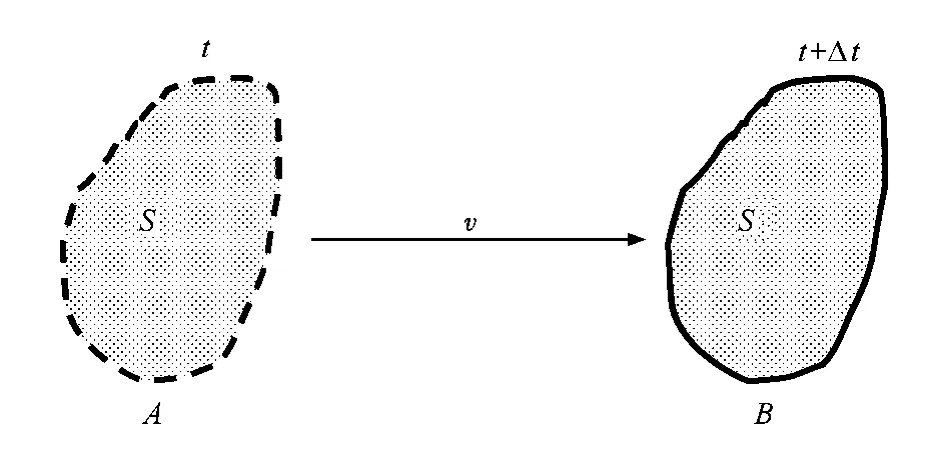
图1 实际接触面积的滑动

在Δt时间内，界面上原子被激励的总次数为

根据量子力学中界面原子能态分立理论，可得界面原子由于相对滑动过程中周期势能场作用而吸收的总能量为

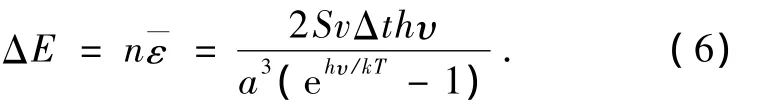
此时原子周围辐射场的频率就是原子受迫振动频率，即υ=v/a，代入(6)式得

设摩擦力为F，摩擦副法向压力为p，摩擦系数为μ，则在Δt时间内摩擦力所做功为

假设摩擦过程中摩擦功全部耗散为系统的热能，则有

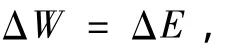
则滑动摩擦系数可表示为

定义p为实际接触面积上的法向应力，p=P/S，则(9)式变为

从(10)式中可以看出，当相对滑动速度趋近于0时，滑动摩擦系数趋于，即静摩擦系数只与原子温升能力及实际接触面积变化有关;而当速度逐渐增大时，在原子温升能力不变的情况下，滑动摩擦系数随相对速度增加而呈缓慢下降趋势.当相对速度较大时，滑动摩擦系数基本不随相对滑动速度的变化而变化.实际上，上述结论是在假设界面原子可能温升不变的前提下得出的，而摩擦过程中存在热力耦合现象，即界面原子温升能力随摩擦速度的变化而变化，因此不能从单因素角度去考虑相对速度对滑动摩擦系数的影响.

根据作者在文献［17］中的研究结论，界面原子温升与相对滑动速度之间存在如下的关系

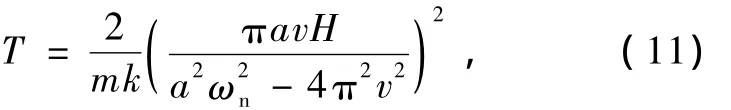
式中，m为原子质量，H为界面势能场激励力幅，ωn为原子固有频率.将(11)式代入(10)式得

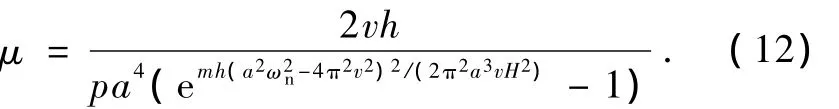
4.分析与讨论

以 α-Fe为例，有 m=9.3 ×10－26kg，a=2.87 ×10－10m，取 ωn=3.0 × 1011rad/s，H=1 × 10－10N.对(12)式进行计算分析.

图2反映了滑动摩擦系数随p值变化的趋势.

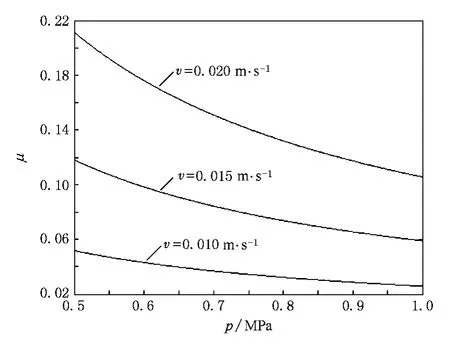
图2 摩擦副法向正应力与滑动摩擦系数关系

显然，当载荷不变时，摩擦界面的实际接触面积愈大，滑动摩擦系数愈高.然而，当载荷较小时，由于实际接触面积与载荷成线性关系，即p为常数，因此载荷增加不会导致滑动摩擦系数增加.而当实际接触面积与名义接触面积接近时，实际接触面积的增加不再与载荷增加成正比关系，即p随载荷的变化而变化.由于载荷增加时实际接触面增大不明显，因此p值随载荷增大而增加，此时，滑动摩擦系数随载荷增大而呈下降趋势，宏观上表现为摩擦力随载荷增大而呈非线性增加.

图3反映了相对滑动速度对滑动摩擦系数的影响.

图3 滑动摩擦系数随相对滑动速度变化曲线

总体上，界面摩擦时滑动摩擦系数随相对滑动速度的增大而增加，且相对速度较低时，滑动摩擦系数随相对速度增大而增加的趋势较小.相对速度愈高，对滑动摩擦系数的影响愈大.文献［10］中指出，在滑动刚发生时，滑动摩擦系数随相对滑动速度增大而减小，当速度继续增大时，又随相对滑动速度增大而增大.显然，该结论在滑动刚开始时与本文分析的结论不一致，而在一定的滑动速度后，其结论是一致的.

实际上，根据量子力学理论，原子在两个定态能级之间发生跃迁时必须满足υ=(En－Em)/h.对于某种原子而言，其不同能态的能量值是分立的，因此能够使原子能态发生改变的外场频率也是离散的.当外场频率为界面势能场激励频率时，表明只有在一些离散的相对滑动速度时，界面原子才能在外场激励作用下有从低能态向高能态跃迁的可能，此时摩擦界面才有摩擦功的耗散.在缓慢滑动时，一方面由于激励频率低于紫外频率时原子能态的量子特性不明显，导致该模型不能准确反映摩擦系数随滑动速度变化的趋势;另一方面，在低速滑动时，由于辐射场能量较小，大部分原子不能吸收辐射场的能量，只有少数原子可能发生能态的跃迁而存在能量的耗散.随着相对滑动速度的增大，辐射场能量增大，可发生能态跃迁的原子数增多，因此耗散的能量增加，表现为滑动摩擦系数增加.

图4为滑动摩擦系数随晶格常数变化的计算曲线.

图4 滑动摩擦系数随晶格常数变化曲线

在其他参数不变的情况下，滑动摩擦系数随晶格常数的增大而降低，且晶格常数愈小其降低趋势愈显著.当晶格常数较大时，其变化对滑动摩擦系数影响较小.此外，摩擦副之间的相对滑动速度愈大，晶格常数的变化对滑动摩擦系数的影响程度愈大.显然，对于晶格常数很小的材料，该结论与文献［9］中的结论存在一定的差异.实际上，当晶格常数增大时，界面原子在周期势能场激励下的激励频率降低，界面原子可吸收的基本能量子数减少，同时，在相对滑动速度不变的前提下，在相同时间内，原子被激励的次数减少，因此摩擦过程中的能量消耗减少，宏观上表现为滑动摩擦系数降低.当晶格常数较大时，滑动摩擦系数随晶格常数变化而变化的程度很小，此时的结论与文献［9］的结论一致.

图5为根据(10)式仿真计算而得到的原子温升与滑动摩擦系数耦合作用关系图.

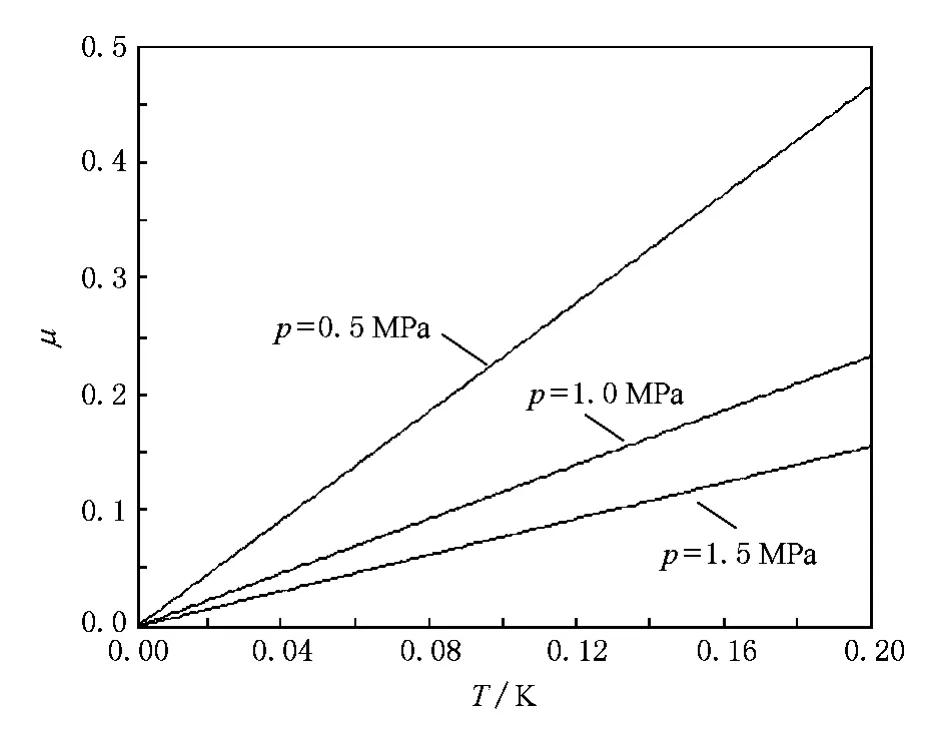
图5 滑动摩擦系数与原子温升耦合关系 计算条件:a=2.87×10－10m，v=0.01 m·s－1

在相对滑动过程中，摩擦功耗散为摩擦热.从微观上看，界面原子随摩擦功耗散而温度升高，温度升高又将影响界面摩擦状态.因此，界面原子温升与摩擦状态存在一定的耦合关系，如图5所示.随着原子可能温升能力增加，滑动摩擦系数呈现出增大的趋势.实际上，在吸收同样能量的前提下，可能温升能力愈强，表明材料的比热容愈小.因此，比热容小的材料，在同等条件下，滑动摩擦系数就愈大.该结论与文献［18］结论基本一致.然而，由于在计算过程中假设摩擦所消耗的能量均被摩擦界面表面层原子吸收，且能量没有传递给其他层原子，因此该结论只是从趋势上反映了界面原子温升与滑动摩擦系数之间的关系.

上述模型所得到的滑动摩擦系数随载荷、相对滑动速度和晶格常数等参数的变化趋势与作者在文献［19］中所建立的滑动摩擦系数模型所得到的趋势一致.前者认为界面原子所具有的能态是非连续的，振子的能态是分立的，相对滑动速度愈高，原子能态的离散性愈明显.因此，理论上相对滑动速度较高时，该模型能更好地描述系统的摩擦特性.后者根据经典力学理论，认为界面原子在外场激励作用下作谐振动，振子所具有的能量是连续的，因此，该模型适应于对缓慢滑动过程中系统摩擦特性的宏观描述.

5.结 论

研究表明，在线弹性接触状态下，滑动摩擦系数与载荷及实际接触面积无关，当实际接触面积接近名义接触面积时，法向正应力随载荷增加而增大，此时滑动摩擦系数随载荷增加而减小.在缓慢滑动时，滑动摩擦系数随滑动速度增高而呈缓慢增大趋势，相对速度愈高，滑动摩擦系数增加趋势愈显著.滑动摩擦系数随晶格常数增加而降低，且晶格常数愈小其降低趋势愈显著，当晶格常数较大时，其变化对滑动摩擦系数影响较小.随着原子可能温升的增加，滑动摩擦系数呈现出增大趋势.因此，材料的比热容愈小，滑动摩擦系数愈大.

［1］Majcherczak D，Dufrenoy P，Berthier Y 2007Tribol.Int.40 834

［2］Robbins M O，Krim J 1998MRS Bulletin23 23

［3］Yoshitsugu K 2000Proceedings of the International Tribology Conference(Volume 1)Nagasaki，Japan，2000 p3

［4］Xie Y B 2001Tribology21 161(in Chinese)［谢友柏 2001摩擦学学报 21 161］

［5］Buldum A，Leitner D M，Ciraci S 1999Phys.Rev.B 59 16042

［6］Ciraci S，Buldum A 2003Wear254 911

［7］Zhang X J，Meng Y G，Wen S Z 2004Acta Phys.Sin.53 728(in Chinese)［张向军、孟永钢、温诗铸 2004物理学报 53 728］

［8］Xu Z M，Huang P 2006J.South China Univ.Tech.34 62(in Chinese)［许中明、黄 平2006华南理工大学学报(自然科学版)34 62］

［9］Xu Z M，Huang P 2006Tribology26 159(in Chinese)［许中明、黄 平2006摩擦学学报26 159］

［10］Bai H B，Zhang P L，Huang X Q 2001Mechanical Sci.Tech.20 346(in Chinese)［白鸿柏、张培林、黄协清2001机械科学与技术 20 346］

［11］Tomlinson G A 1929Phil.Mag.Ser.7 905

［12］Xu Z M，Huang P 2006Acta Phys.Sin.55 2427(in Chinese)［许中明、黄 平 2006物理学报 55 2427］

［13］Lin M M，Duan W S，Chen J M 2010Chin.Phys.B 19 026201

［14］Gong Z L，Huang P 2008Acta Phys.Sin.57 2352(in Chinese)［龚中良、黄 平 2008物理学报 57 2352］

［15］Ding L Y，Gong Z L，Huang P 2009Acta Phys.Sin.58 8522(in Chinese)［丁凌云、龚中良、黄 平 2006物理学报 58 8522］

［16］Yang F J 2001The Atomic Physics(Beijing:High Education Press)(in Chinese)［杨福家2001原子物理学 (北京:高等教育出版社)］

［17］Gong Z L，Ding L Y，Huang P 2008Tribology28 322(in Chinese)［龚中良、丁凌云、黄 平 2008摩擦学学报 28 322］

［18］Majcherczak D，Dufrenoy P，Berthier Y 2007Tribol.Int.40 834

［19］Gong Z L，Huang P 2008J.South China Univ.Tech.36 10(in Chinese)［龚中良、黄 平2008华南理工大学学报(自然科学版)36 10］

PACS:46.55.+d，81.40.Pq

A calculating model of sliding friction coefficient based on non-continuous energy dissipation*

Gong Zhong-Liang1)†Huang Ping2)
1)(College of Mechanical and Electrical Engineering，Central South University of Forestry and Technology，Changsha 410004，China)
2)(School of Mechanical and Automotive Engineering，South China University of Technology，Guangzhou 510640，China)
(Received 16 March 2010;revised manuscript received 23 May 2010)

A sliding friction coefficient calculation model was established based on analysis of non-continuous diffusion of energy during the interfacial friction.The results indicated that the sliding friction coefficient is not related with the load and the actual contact area under elastic contact.However，when the actual contact area is close to the nominal contact area，the sliding friction coefficient will increase along with the reducing load.When sliding is slow，the friction coefficient rises slowly with the increase of the sliding velocity，and the influence is more remarkable when the sliding speed is higher.Furthermore，the larger the atomic lattice，the smaller the sliding friction coefficient is.The sliding friction coefficient increases with the rising of the atomic temperature.These results will be used to engineering application and theoretical research.

sliding friction coefficient，non-continuous energy dissipation，interfacial friction

*国家自然科学基金(批准号:50875087)和清华大学摩擦学国家重点实验室开放基金(批准号:SKLTKF08B04)资助的课题.

*Project supported by the National Natural Science Foundation of China(Grant No.50875087)and the Tribology Science Fund of State Key Laboratory of Tribology of Tsinghua University，China(Grant No.SKLTKF08B04).