平面柔性梁的刚-柔耦合动力学特性分析与仿真*
和兴锁 李雪华 邓峰岩
(西北工业大学工程力学系,西安 710072)
(2010年1月31日收到;2010年5月3日收到修改稿)
平面柔性梁的刚-柔耦合动力学特性分析与仿真*
和兴锁†李雪华 邓峰岩
(西北工业大学工程力学系,西安 710072)
(2010年1月31日收到;2010年5月3日收到修改稿)
针对大范围运动规律为未知的刚-柔耦合系统研究其动力学特性.利用有限元方法对柔性梁进行离散,采用Lagrange方程建立平面柔性梁的刚-柔耦合动力学方程,研究在大范围运动为自由情况下,平面柔性梁的大范围运动和变形运动的相互耦合机理,比较零次模型、一次耦合模型及精确模型的差异,探讨各种模型的适用性.
平面柔性梁,刚-柔耦合系统,动力学特性,分析与仿真
PACS:45.10.- b,05.45.- a,45.05.+x
1.引 言
文献[1,2]针对非惯性坐标系下大范围运动规律为已知的柔性梁结构进行了研究,在这类研究中,刚体运动是作为已知运动出现的,表征刚体运动的坐标并不出现在系统的动力学方程中,因此实际上这类刚-柔耦合动力学研究的是单向问题,即只考虑了大范围运动对柔性结构的影响,而未考虑柔性体的变形对刚体运动的影响.但在工程实际中,刚体运动规律未知的刚-柔耦合结构也大量存在于实际机构中,如给定驱动力矩的柔性机械臂等结构.因此这类考虑刚-柔部件之间相互耦合作用的动力学问题也受到研究者越来越多的重视[3—5].同时,对中心刚体-卷簧-柔性梁这类典型结构,有研究者也进行了一些理论和实验研究[6—8].以往的研究在一定程度上为工程实际应用做好了理论准备[9,10].
但以往的研究未考虑完全的几何非线性变形模式,其动力学方程及实验比较是建立在一次耦合模型基础上的,因此只探讨了零次模型和一次耦合模型的差异,以及耦合模型与刚体模型之间的差异,并未探讨耦合模型之间的差异.本文将对这些问题进行深入的研究.
2.平面柔性梁的刚-柔耦合动力学特性分析
图1所示为一固结在旋转中心刚体上的平面悬臂柔性梁,中心体半径为 R,转角为 θ,角速度为 θ·,角加速度为θ¨,中心刚体的转动惯量为 J0,中心刚体与机架之间装有刚度为K0的扭转弹簧,该模型为研究刚-柔耦合动力学问题的典型模型.

图1 由中心刚体-柔性梁-扭簧组成的刚-柔耦合系统
对于大范围运动规律未知,系统广义坐标为

式中qf表示节点的位移.中心刚体动能和扭转弹簧势能分别为
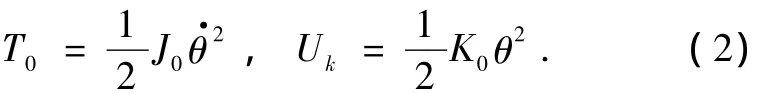
不计分布外力,利用有限元离散后,采用 Lagrange方程可得刚-柔耦合系统的动力学方程为

式中的广义质量阵M和广义力阵Q分别为

广义质量阵M和广义力阵Q 中的各参量分别为
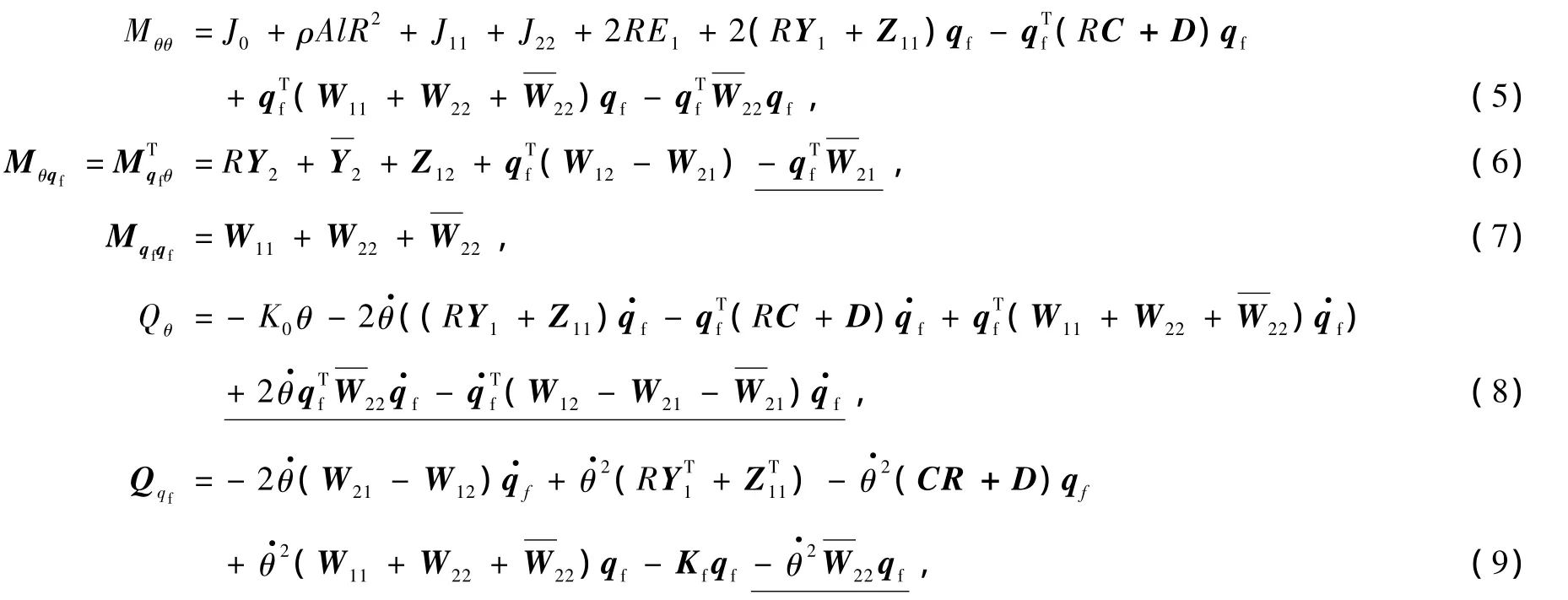
式中J0为中心刚体转动惯量,A和l分别为梁的横截面积和长度,ρ为密度,E为弹性模量.ρlIyy,Iyy和Izz为横截面的惯性矩.K0为卷簧刚度,Kf为弹性梁固有弹性刚度阵.Y,Z,W,C,D等表示式见文献[5].
本文精确模型与一次耦合模型相比,增加了变形耦合项,即上述各式中的划线项.另外,一次耦合模型和本文精确模型比零次耦合模型均增加了耦合项C和D.
现取梁的物理参数为:中心刚体半径为 R=1 m,长度为l=8 m,弹性模量为 E=6.8952×1010N/m2,密度为 ρ=2.766×103kg/m3,横截面积为 A=7.2986×10-5m2,横截面惯性矩为 IZZ=8.2189×10-9m4.
1)当端点无初始变形,初始角度 θ(0)=0.01 rad,初始角速度(0)=0 rad/s,中心刚体转动惯量 J0=30 kg·m2时,改变卷簧刚度 K0.零次模型、一次耦合模型和本文精确模型的计算仿真结果如图2所示.
由图2可知,当 K0=200 N·m/rad时,三种模型的仿真结果几乎没有差别.
根据文献[7],第一阶频率为扭转弹簧产生的中心刚体大范围运动的振动频率,第二阶频率为柔性梁振动产生的一阶频率.三种模型下,第一、二阶频率几乎无差别,均为0.2188和0.7813 Hz.增加卷簧刚度至K0=1000 N·m/rad,计算仿真结果如图3所示.
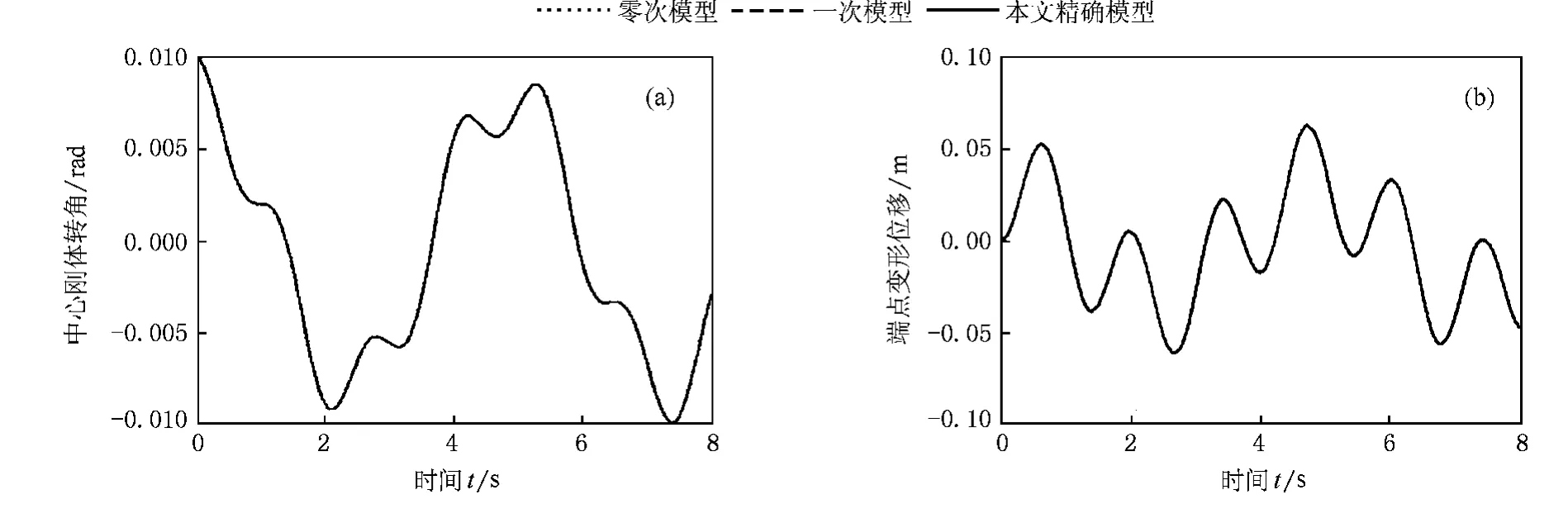
图2 K0=200 N·m/rad,J0=30 kg·m2,θ(0)=0.01 rad时,中心体转角以及梁端点在 方向的变形位移 (a)中心刚体转角,(b)端点变形位移
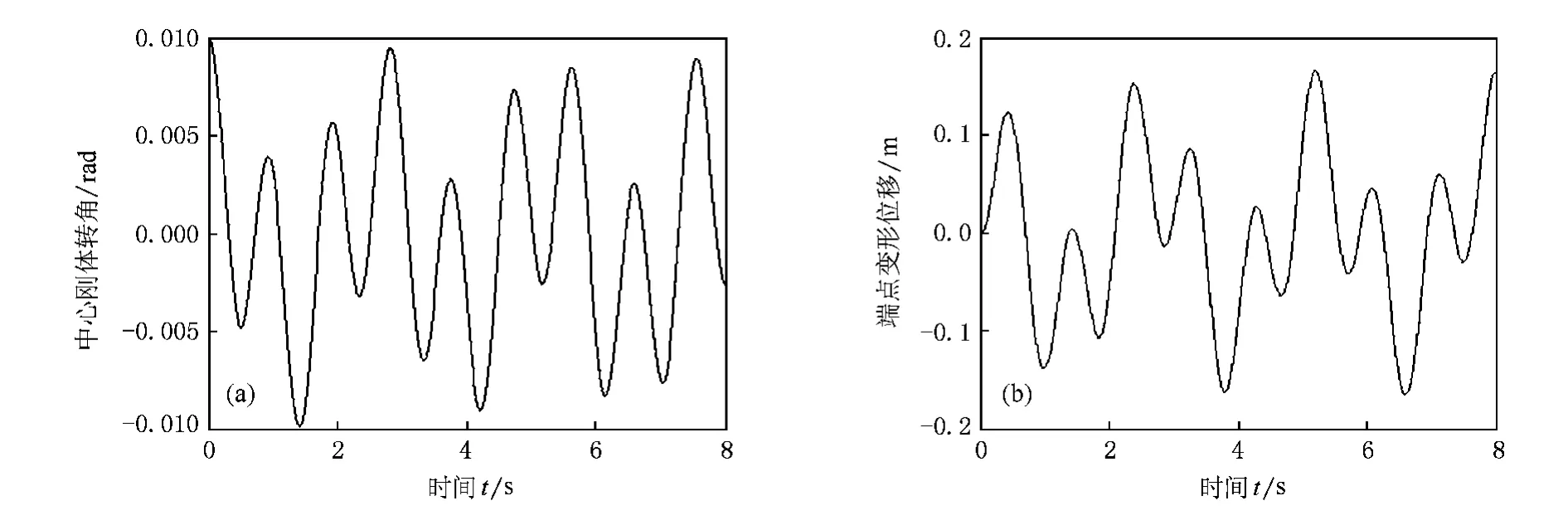
图3 K0=1000 N·m/rad,J0=30 kg·m2,θ(0)=0.01 rad时,中心体转角以及梁端点在 e12方向的变形位移 (a)中心刚体转角,(b)端点变形位移
由图3曲线可见,即便加大弹簧刚度,三种模型的转角响应、端点位移响应几乎没有差别.计算仿真结果同时表明,三种模型的第一、第二阶频率都变大,但几乎没有差别,依次为0.375和1.0625 Hz.因此在初始角较小的情况下,刚-柔刚度比[7]Kp=K0l/EIzz,对三种模型几乎没有影响.
2)当端点无初始变形,初始角度 θ(0)=0.01 rad,初始角速度(0)=0 rad/s,卷簧刚度 K0=200 N·m/rad,中心刚体转动惯量 J0=3 kg·m2时,计算仿真结果如图4所示.由图示曲线可见,减小中心刚体转动惯量,对三种模型的转角响应和端点位移响应几乎没有差别.三种模型的第一、二阶频率都比相同刚度下变大,但它们之间几乎没有差别,依次为0.25和1.5313 Hz.因此在初始角较小的情况下,刚柔惯量比[7]Jp=J0/Jb,对三种模型几乎没有影响.其中 Jb=ρAl3/12+ρAl(0.5+R)2为梁未变形时,相对于中心转轴的转动惯量.此外由于中心体转动惯量的减小,柔性梁的高阶频率(第三阶频率)被激发出来,但其对中心刚体和柔性梁的振动贡献较小.
计算与仿真结果表明,本文精确模型与一次耦合模型差异不明显,说明对于平面刚-柔耦合系统,在基点运动速度和中心刚体大范围运动都较小的情况下,新增的变形耦合项作用较弱.随着卷簧刚度的增加和中心体转动惯量的减小,中心体的转角和梁的端点位移振动幅值变大且波动加剧.
中心刚体初始转角增加后,一次耦合模型和本文精确模型的端点位移响应、转角响应以及频率几乎没有差别,但这两种模型与零次模型的差别变得明显.本文精确模型与一次耦合模型的第一阶频率为0.2344 Hz,而零次耦合模型第一阶频率为0.2266 Hz;本文精确模型与一次耦合模型的第二阶频率为0.8125 Hz,而零次耦合模型第二阶频率为0.7188 Hz.观察中心刚体的角速度响应,如图6所示.
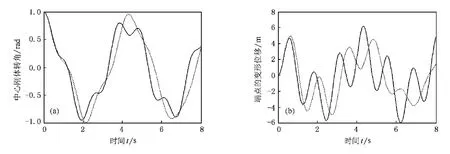
图5 K0=200 N·m/rad,J0=30 kg·m2,θ(0)=1 rad时,中心体转角以及梁端点在方向的变形位移 (a)中心刚体转角,(b)端点变形位移

图 6 K0=200 N·m/rad,J0=30 kg·m2,θ(0)=1 rad 时,中心刚体转动角速度
初始角度变大后,中心体转速较高,中心体运动范围也变大,角速度峰值接近2 rad/s,可见在角速度较大情况下,耦合项C,D作用明显,使得柔性梁产生动力刚化现象,对应刚-柔耦合的中心刚体-柔性梁结构,即第二阶频率增加;对于中心刚体的振动频率(第一阶频率)而言,耦合项 C,D也起到一定的作用.
改变K0和R以获得不同刚柔刚度比Kp和刚柔惯量比Jp,比较不同初始角下的第一、二阶频率,如表1和表2所示.表中,一次耦合模型和本文精确模型统称为耦合模型.
3.算例结果分析
在相同刚柔刚度比或刚柔惯量比的情况下,当初始角较大时,角速度变化增大,中心体运动范围变大,零次模型和耦合模型的第一、二阶频率呈现差异.第二阶频率对应为柔性梁的振动频率,与零次模型相比,由于C,D项的作用,耦合模型产生了动力刚化现象,随着初始角的增加,该阶频率逐渐变大,而零次模型的该阶频率逐渐变小.此外,第一阶频率为扭转弹簧产生的中心刚体大范围运动的振动频率,零次模型的该阶频率保持不变,耦合模型的该阶频率在初始角较大情况下会升高.相对于第二阶频率,耦合模型的第一阶频率只有在初始角较大的情况下,如表1中初始角为1 rad时才会有所提高,而第二阶频率在相同刚柔刚度比或刚柔惯量比的情况下,具有较小的初始角就会有所提高,如表1中初始角为0.5 rad时.这说明耦合模型下能够反映大范围运动对刚体振动的影响,同时柔性梁的振动受系统的大范围影响较大,在柔性梁振动为主的情况下,耦合模型的动力刚化现象较明显.
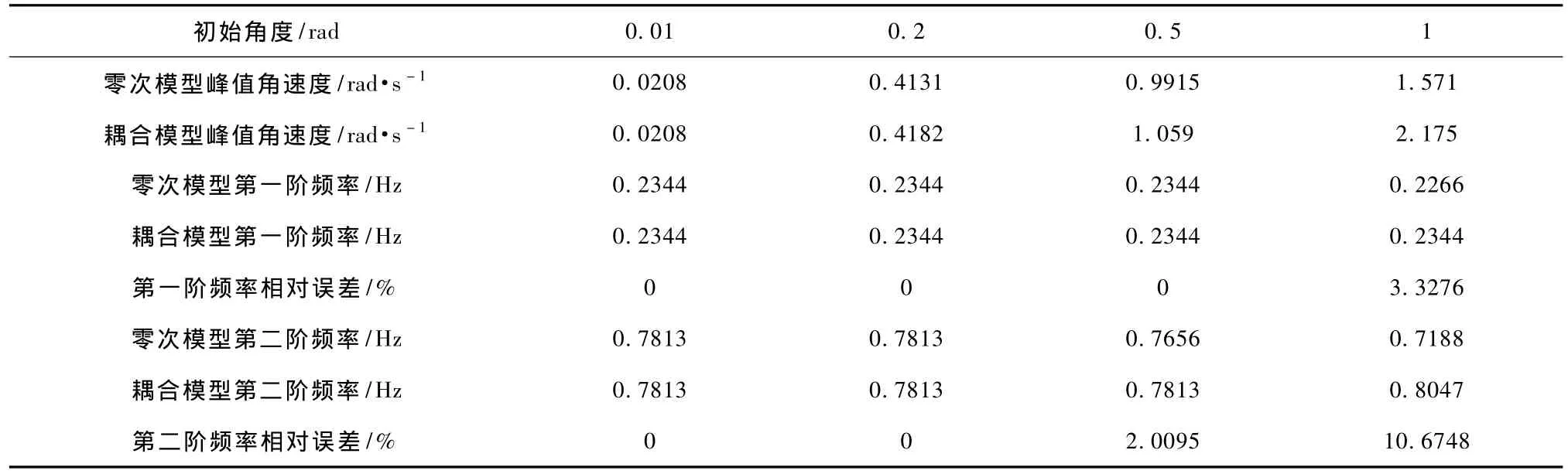
表1 Kp=K0l/EIzz=2.82332,Jp=J0/Jb=0.612378时,初始角对系统频率的影响
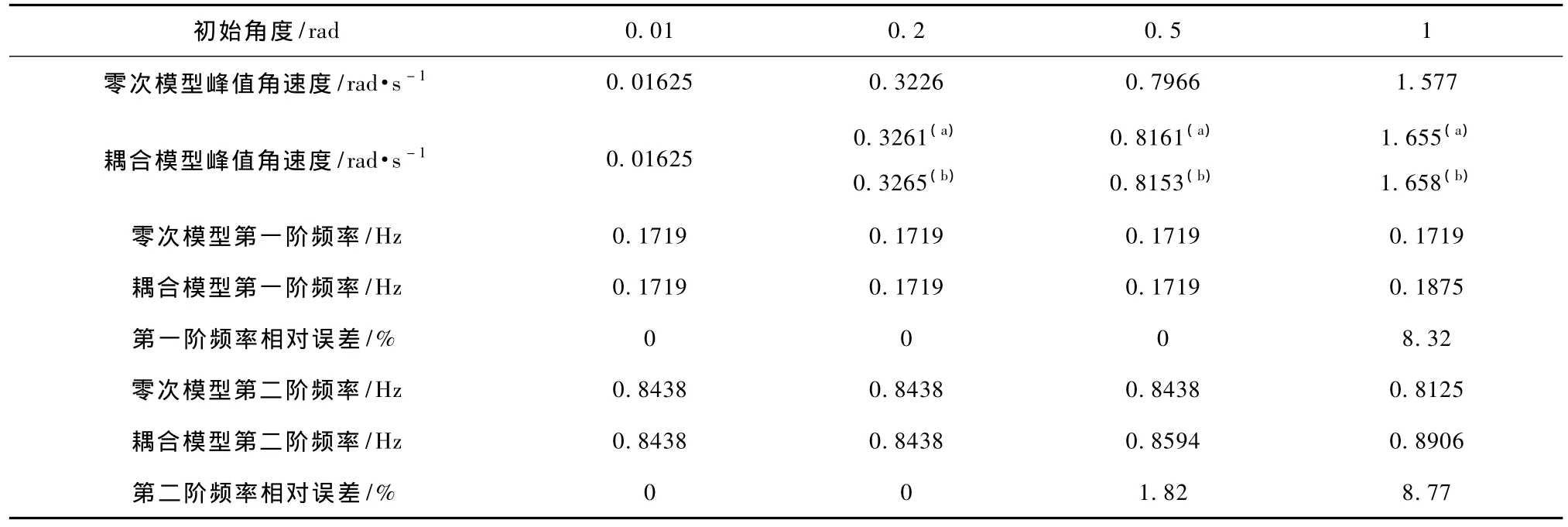
表2 Kp=K0l/EIzz=2.82332,Jp=J0/Jb=0.267915时,初始角对系统频率的影响
在初始角增幅较小的情况下,角速度变化较小,中心体运动范围较小,若此时刚柔刚度比较大或刚柔惯量比较小,耦合模型的第二阶频率仍会较零次模型变大,如表2在初始角为0.2 rad时,两种模型就呈现了差异,这也说明柔性梁的频率受系统运动的影响较大.
对于转角、端点位移以及频率响应,无论初始角度如何,即无论刚体运动范围是否变大,一次耦合模型与本文精确模型差别很小,说明对于大范围运动为未知的平面刚-柔耦合结构而言,变形的相互耦合作用以及基点速度和角速度的耦合作用并不明显,这不同于非惯性系下大范围运动为已知的平面刚-柔耦合结构.
4.结 论
本文对大范围运动规律为未知的中心刚体-柔性梁-扭簧这一典型的刚-柔耦合结构进行了研究.与零次模型和一次耦合模型相比,本文精确模型下动力学方程包含了完整的耦合项.
研究发现,在初始角度较大,即系统具有较大的运动速度和大范围刚体运动时,零次模型与一次耦合模型和本文精确模型会出现差异,一次耦合模型和本文精确模型能够体现出动力刚化效应,其高阶频率会随着大范围运动的增加而上升,而零次模型则相反.对于平面刚-柔耦合结构,一次耦合模型与本文精确模型的仿真结果差异不大,说明新增的变形耦合项作用不明显.因此对于大范围运动为未知的刚柔耦合结构,其大范围运动的速度和幅度依然是决定动力学特性和动力学模型适用的重要因素.在非惯性系下的动力刚化效应,也存在于运动规律未知的刚-柔耦合结构中.
[1]He X S,Deng F Y 2010Acta Phys.Sin.59 25(in Chinese)[和兴锁、邓峰岩2010物理学报 59 25]
[2]Deng F Y,He X S,Li L,Zhang J 2007Multibody Syst.Dyn.18 559
[3]Liu Y Z 2009Chin.Phys.B 18 1
[4]Meng Z,Liu B 2008Acta Phys.Sin.57 1329(in Chinese)[孟 宗、刘 彬2008物理学报57 1329]
[5]He X S,Deng F Y,Wang R 2010Acta Phys.Sin.59 1434(in Chinese)[和兴锁、邓峰岩、王 容 2010物理学报 59 1428]
[6]Fu J L,Chen B Y,Tang Y F,Fu H 2008Chin.Phys.B 17 3942
[7]Yang H 2002Ph.D.Dissertation(Shanghai:Shanghai Jiao Tong University)(in Chinese)[杨 辉 2002博士学位论文(上海:上海交通大学)]
[8]Liu J Y 2000 Ph.D.Dissertation(Shanghai:Shanghai Jiao Tong University)(in Chinese)[刘锦阳2000博士学位论文(上海:上海交通大学)]
[9]Xue Y,Weng D W 2009 Acta Phys.Sin.58 34(in Chinese)[薛 纭、翁德玮 2009物理学报 58 34]
[10]Bai C L,Zhang X,Zhang L H 2009 Chin.Phys.B 18 475
PACS:45.10.- b,05.45.- a,45.05.+x
Analysis and imitation of dynamic properties for rigid-flexible coupling systems of a planar flexible beam*
He Xing-Suo†Li Xue-Hua Deng Feng-Yan
(Department of Engineering Mechanics,Northwestern Polytechnical University,Xi'an 710072,China)
(Received 31 January 2010;revised manuscript received 3 May 2010)
The finite element method is used for the system discretization and the coupling dynamic equations of flexible beam are obtained by Lagrange's equations.The second order coupling terms between rigid large overall motion,arc length stretch,lateral flexible deformation kinematics and torsional deformation terms are included in the present exact coupling model to expand the theory of one-order coupling model.The dynamic response of the present model is compared with that of zero-order approximate model and one-order coupling model.Then the changes of dynamic stiffening terms due to the new coupling terms are discussed according to different models.At the same time,the effect of initial static deformation in the tip is considered to study the vibrant deformation of flexible beam.The difference between zero-order approximate model,one-order coupling model and the present exact model is revealed by the frequency spectrum analysis method and it is concluded that the speed of overall motion is a vital cause for the difference between different models.And we found that the dynamic stiffening phenomenon still exists in rigid-flexible coupling system while the overall motion is free.But the effect of dynamic stiffening in the present exact model is not as severe as that in the one-order coupling model.
planar flexible beam,rigid-flexible coupling systems,dynamic properties,analysis and imitation
*国家自然科学基金(批准号:10672133)资助的课题.
*Project supported by the National Natural Science Foundation of China(Grant No.10672133).

