基于Darcy-Stokes耦合模型的缝洞型介质等效渗透率分析

李亚军,姚 军,黄朝琴,刘永辉

(中国石油大学石油工程学院,山东青岛266555)

基于Darcy-Stokes耦合模型的缝洞型介质等效渗透率分析

李亚军,姚 军,黄朝琴,刘永辉

(中国石油大学石油工程学院,山东青岛266555)

根据缝洞型介质的特点和流体在不同尺度空间的流动特征,建立Darcy-Stokes耦合数学模型,推导出考虑基岩渗透率的广义立方定律和单裂缝多孔介质的等效渗透率张量表达式,以此为基础提出裂缝预处理技术,将溶洞-裂缝-基岩耦合流动问题转化为溶洞-基岩耦合流动问题,分析不同缝洞结构介质体的等效渗透率和渗透特性。结果表明:缝洞结构的存在不同程度地影响介质体的等效渗透率;含圆形溶洞介质的等效渗透率与基岩渗透率成线性关系;裂缝预处理技术可以提高计算效率。

缝洞型介质;Darcy-Stokes耦合模型;连续介质;等效渗透率;流动模拟

缝洞型介质是基岩孔隙、裂缝和溶洞交叠嵌套分布的多尺度复杂固体介质,在油气田开发、水利科学和生物科学中,许多问题的研究对象都具有缝洞型介质的特征[1-3]。缝洞型介质具有多尺度性和非均质性,其渗透率与多孔介质相比存在较大差异。缝洞型介质内的流动状态和流动规律异常复杂,缝洞内的自由流动和基岩中的渗流共存[4],Saffman[5]在Beavers和Joseph[6]实验研究的基础上,从理论上验证了其实验结论,并通过理论修正得到了Beavers-Joseph-Saffman滑移速度边界条件(简称BJS条件),得到广泛应用,在此基础上形成了Darcy-Stokes耦合模型[7]。耦合模型的数值解法主要有单域法和两域法,单域法是指在整个区域上取统一的速度有限元空间进行分析,如采用标准有限元法[8]或混合有限元法[9],两域法是指在两个区域分别取不同的速度有限元空间,如采用Galerkin法和混合有限元耦合的数值解法[10]。单域法容易进行理论和计算分析,但其有限元空间构造复杂,不利于实际计算;两域法在理论和数值分析时较困难。笔者根据缝洞型介质的特点和流体在不同尺度空间的流动特征,建立Darcy-Stokes耦合数学模型,基于非协调Crouzeix-Raviart型三角形有限元格式建立模型的数值解法,分析不同缝洞结构对介质体等效渗透率和渗透特性的影响。

1 数学模型

如图1(a)所示,将整个缝洞型介质研究区域Ω分解为多孔介质基岩区域Ωd和自由流动区域Ωs,其中Ωs包含裂缝区域Ωf和溶洞区域Ωv,即Ω=Ωd∪Ωs,Ωs=Ωf∪Ωv,各区域的边界表示为∂Ωb(b=d,s,f,v);正方形网格块的边界称为外边界Γj(j=1,2,3,4),nj为相应外边界Γj的单位外法向量。

根据等效原则和等效渗透率计算原理[11],缝洞型非均质离散介质体的等效渗透率(k)可由满足等效原则的均质各向异性连续介质体(图1(b))的渗透率表示。

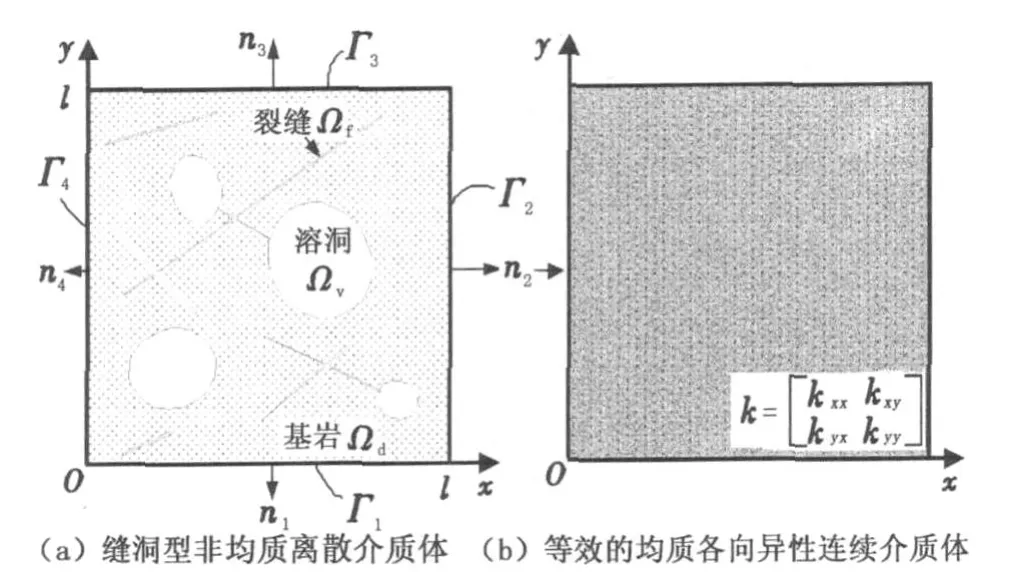
图1 缝洞型介质等效示意图Fig.1 Equivalent schematic diagram of fractured-vuggy media

1.1 控制方程

多孔介质区域Ωd和自由流动区域Ωs的控制微分方程分别表示如下:

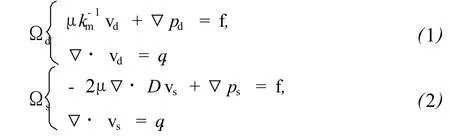
其中

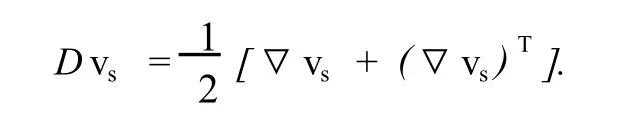
式中,μ为流体动力黏度,Pa·s;km为多孔介质渗透率,m2;vd为多孔介质区域渗流速度,m/s;pd为多孔介质表征单元体中的平均压力,Pa;f为单位体积力,N/m3;q为源汇项;vs为自由流动区域流体速度,m/s;ps为自由流动区域流体压力,Pa;Dvs为变形速率张量。

1.2 边界条件

Darcy-Stokes耦合模型的关键在于建立多孔介质区域与自由流动区域交界面Γ=∂Ωd∩∂Ωs耦合条件,采用BJS条件并结合法向流速连续条件和法向应力连续条件,交界面Γ处的边界条件表示为

其中,ns为∂Ωs的单位外法向量;τ为∂Ωs的单位切向量;α为滑移系数,取决于交界面处的多孔介质的几何特征和结构特征,为无量纲常数。

外边界条件对于准确求解等效渗透率张量非常重要,采用周期边界条件可以保证得到符合物理意义的渗透率张量[12]。整个缝洞型介质研究区域Ω的周期边界条件表示为

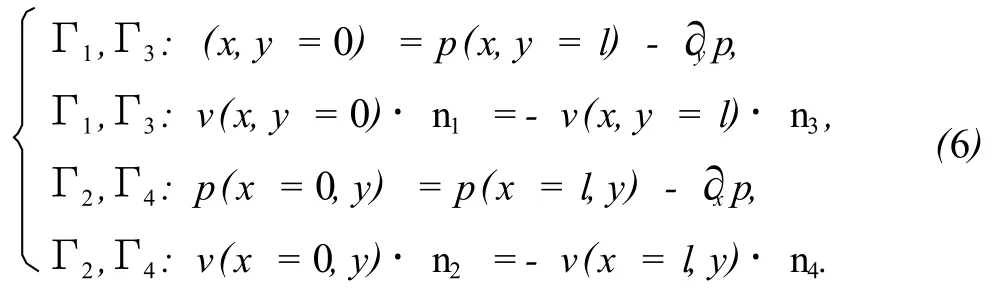
1.3 裂缝预处理方法

对于实际缝洞型介质的流动,由于裂缝数量较多,且裂缝开度尺寸与研究区域的数量级相差较大,为得到较精确的解,裂缝区域剖分的网格须足够密。针对水平单裂缝及其周围多孔介质(图2),考虑基岩渗透率,得到广义立方定律和单裂缝多孔介质的等效渗透率,利用等效渗透率张量表征的连续介质体代替原裂缝介质进行计算。

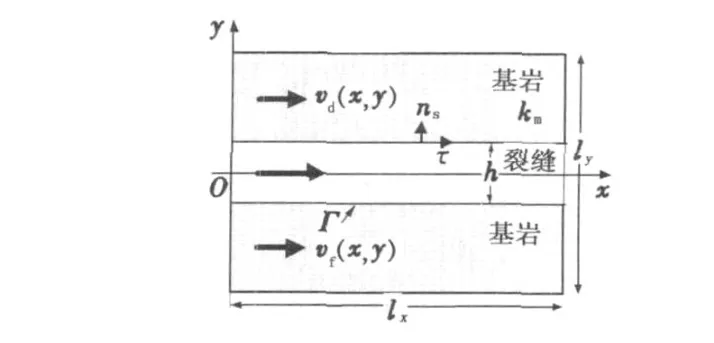
图2 单裂缝多孔介质示意图Fig.2 Schematic diagram of single fractured porousmedia

假定在系统横向和纵向分别施加单位压力梯度,则单位黏度流体通过系统后的速度的解析解分别为

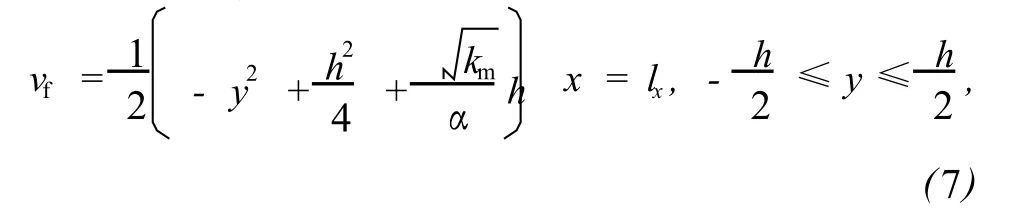
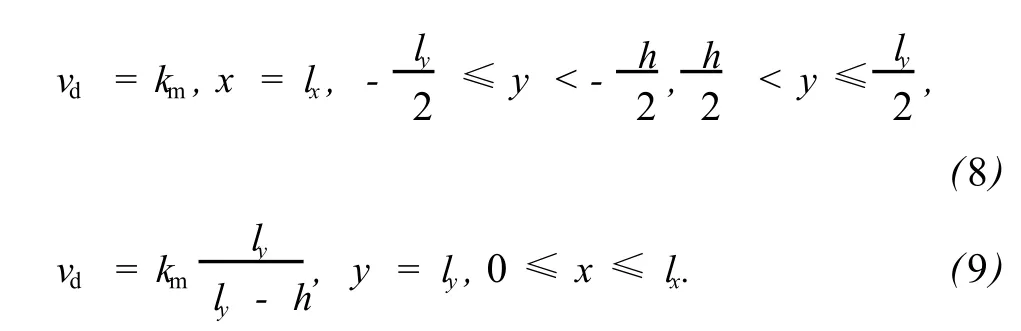
其中,式(7)表示x方向裂缝内的流体速度分布;式(8)表示x方向基岩内的流体速度分布;式(9)表示y方向基岩内的流体速度分布,即单裂缝多孔介质y方向的平均速度。

根据平均速度计算公式[11],得到单裂缝多孔介质在x方向的平均速度为

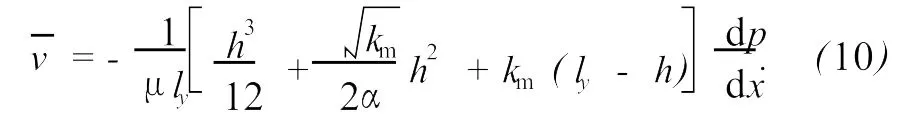
此即为考虑基岩渗透率的单裂缝多孔介质的广义立方定律。根据达西公式的形式,得单裂缝多孔介质系统在x方向和y方向的等效渗透率kfx和kfy为

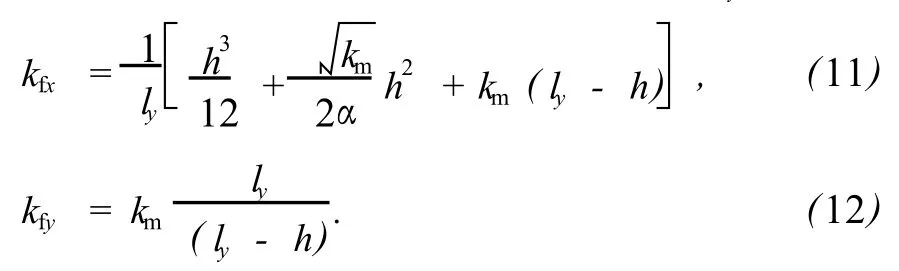
忽略式(11)右端第二项,则变成经典连续条件(仅考虑基岩和溶洞交界面处的法向速度而忽略切向速度)[5]时的解析解。对裂缝方位角θ≠0的情况,则根据渗透率张量转换公式[13]求得等效渗透率张量为

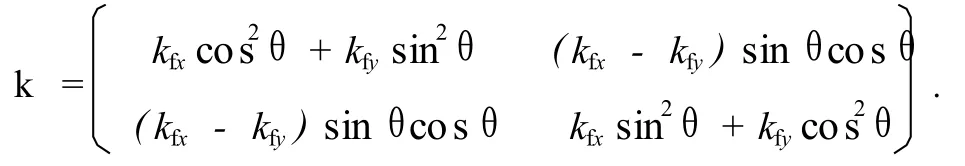
计算每条裂缝及其周围多孔介质区域的等效渗透率张量,利用等效渗透率张量表征的连续介质体代替原裂缝介质,将溶洞-裂缝-基岩耦合流动问题转化为溶洞-基岩耦合流动问题。

令Qd和Qs分别代表多孔介质区域和自由流动区域的流动控制微分方程(1)和(2),则在原始缝洞型介质研究区域上的积分表达式为

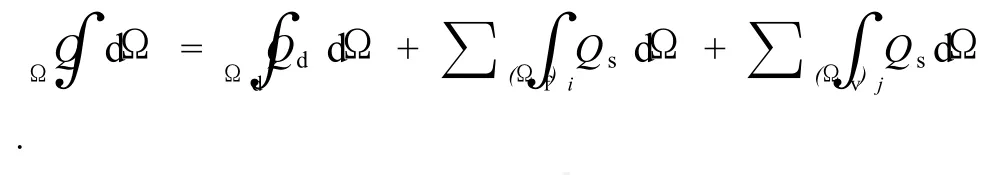
对裂缝进行简化后,其积分表达式变为

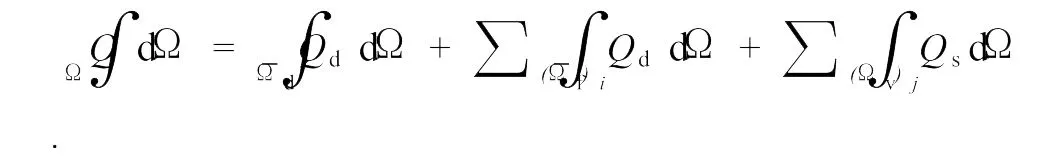
基于非协调元中自由度最小的Crouzeix-Raviart型三角形元,采用稳定化有限元法对Darcy-Stokes耦合问题进行数值求解,此方法与压力常数单元结合自动满足inf-sup条件和质量守恒条件,Feng等[14]严格证明了该方法的稳定性和收敛性,在L2范数下,速度的计算误差阶数为2,压力的为1。

2 计算实例

2.1 含水平单裂缝介质

如图2,多孔介质中含水平贯穿裂缝,lx=ly=8 cm,km=10×10-3μm2,α=1。利用所给出的数值解法和式(11)、(12)分别计算不同裂缝开度时裂缝介质的等效渗透率张量,并与考虑经典连续条件所计算的解析解进行对比,验证数值算法的正确性。计算结果见表1。

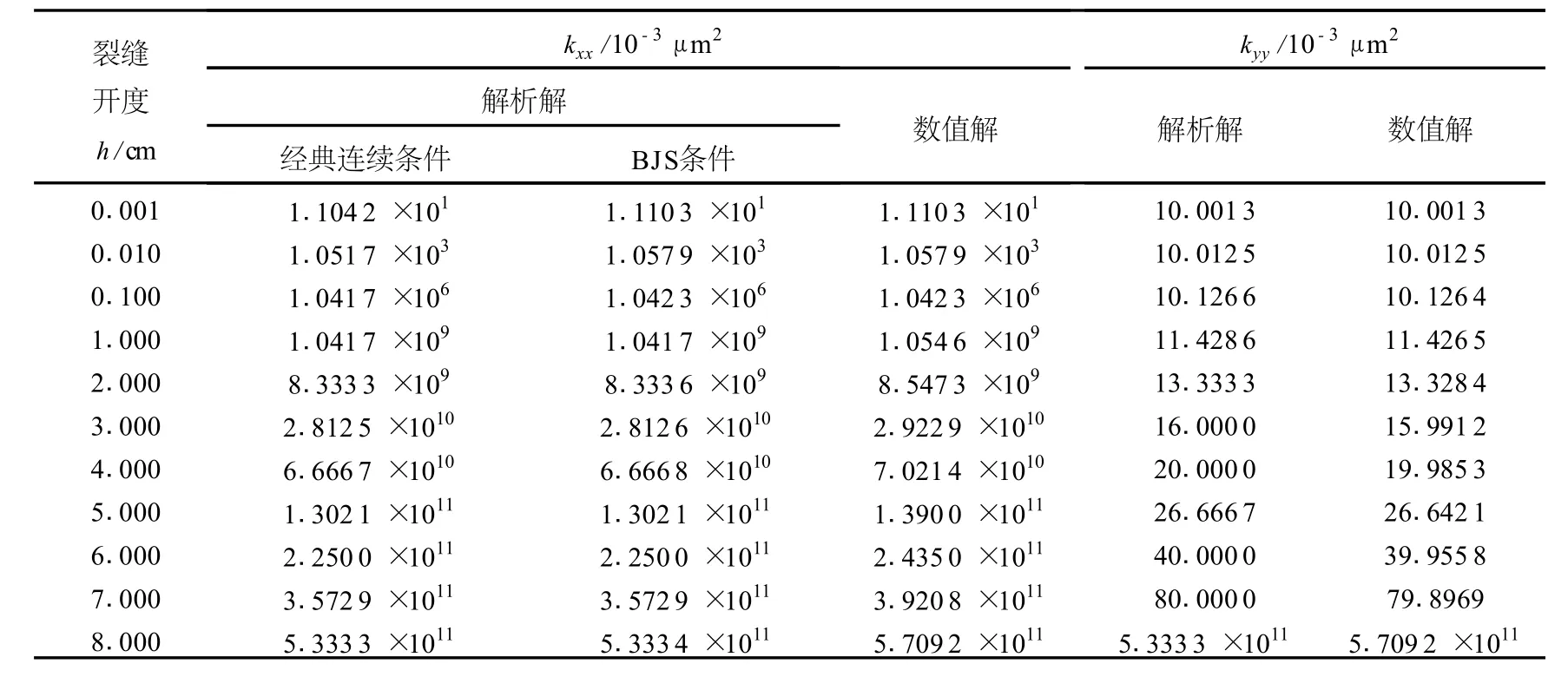
表1 水平单裂缝介质的等效渗透率主值Table 1 Principlal value of equivalent permeability of porous media containing single horizontal fracture

比较发现:解析解与数值解基本一致,证明了数值解法的正确性;随着裂缝开度的增大,kxx急剧增大,而kyy变化较为缓慢;经典连续条件和BJS条件下kxx的解析结果显示,是否考虑基岩和溶洞交界面处的切向速度对最终等效渗透率的计算结果影响不大,而在缝洞型介质流动模拟的计算中,忽略切向速度将使问题容易处理;在确定垂直于裂缝延伸方向的等效渗透率系数时,相当于将裂缝视为具有无限渗透能力,其内部流体为等势体;裂缝开度越小,裂缝在整个流动区域所占比重越小,即纯流体流动区域所占比例较小,则利用Darcy定理描述整个区域的流体流动误差越小,数值计算结果越接近解析结果;当整个研究区域皆为自由流动区时,相当于利用立方定律描述其渗透性。

2.2 含圆形溶洞介质

如图3,边长为1.5 cm的正方形区域中心为一半径为rvug的圆形溶洞,周围为渗透率为km的多孔介质。由于对称性,溶洞介质的等效渗透率的主值相等,即kxx=kyy。不同尺寸溶洞下基岩渗透率与等效渗透率的关系见图4,不同基岩渗透率时溶洞尺寸与等效渗透率的关系见图5。

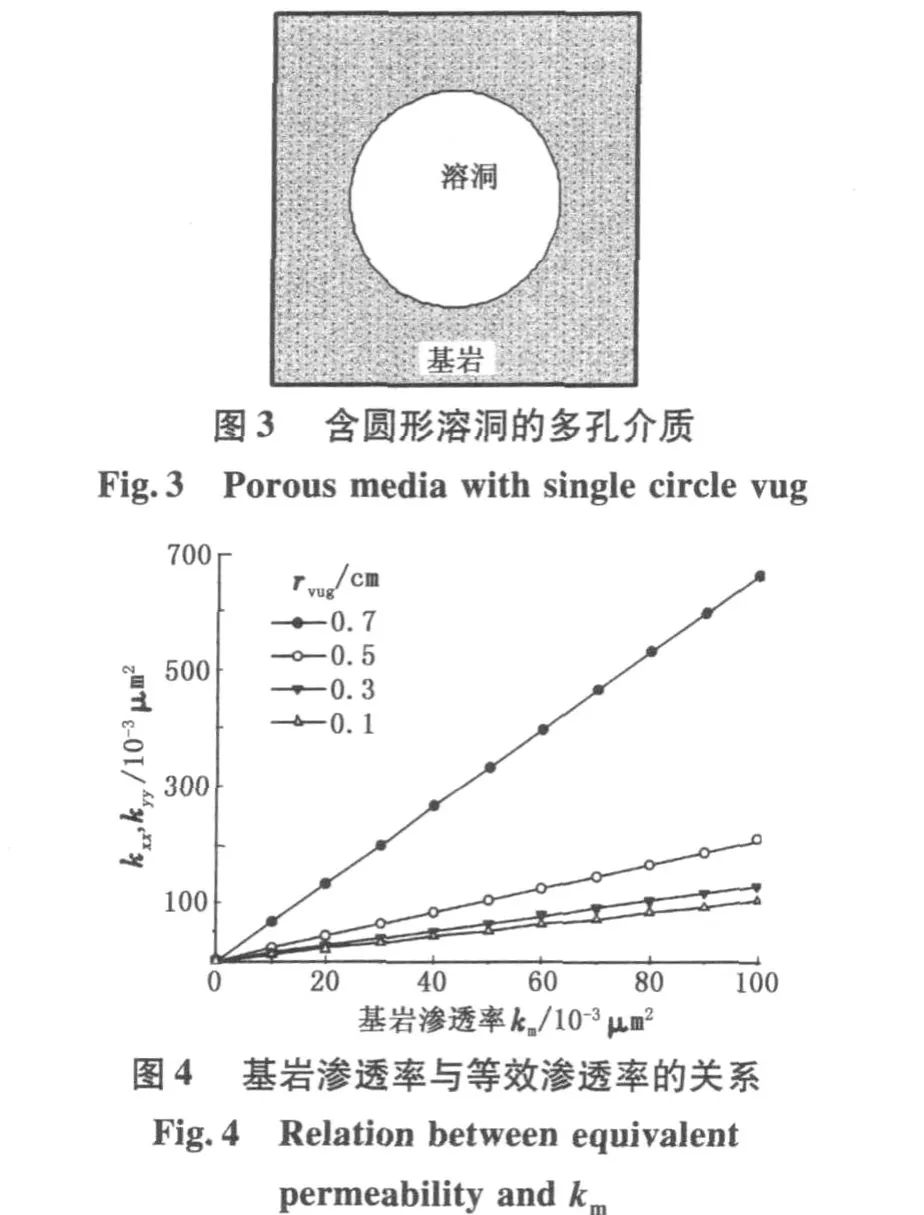
由图4可看出,对相同结构的溶洞介质,其等效渗透率随基岩渗透率的增大而增大,并成线性关系,且溶洞半径越大,直线的斜率越大。由图5可看出:在基岩渗透率保持不变的情况下,当溶洞半径相对较小时,其等效渗透率变化缓慢,而当溶洞尺寸接近外边界时,等效渗透率快速增加;基岩渗透率较小时,溶洞的渗透性受到较大限制,与基岩渗透率较大的情形相比,等效渗透率变化较为缓慢。

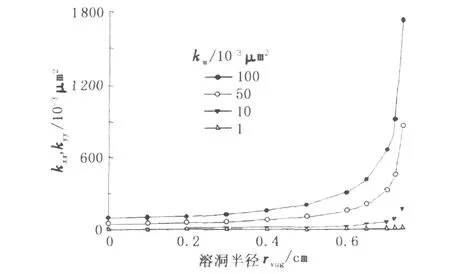
图5 溶洞尺寸与等效渗透率的关系Fig.5 Relation curve between equivalent permeability andrvug

2.3 复杂缝洞型介质

如图6,边长l=12 cm的正方形缝洞型介质,基岩渗透率为100×10-3μm2,内含8条裂缝fi(i=0,1,…,7)和3个溶洞,所有裂缝的开度h=1 000 μm,裂缝f0的倾角β=30°,方形溶洞的尺寸为2.5 cm×8 cm,圆形溶洞的半径为1.5 cm。

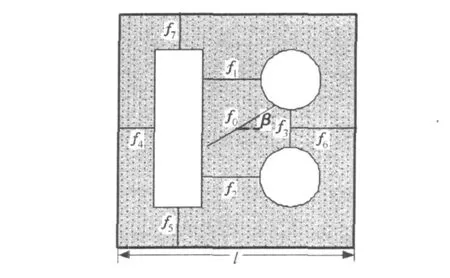
图6 复杂缝洞型介质Fig.6 Complicated fractured-vuggy media

分别计算如下4种介质系统的等效渗透率张量:(Ⅰ)介质体内仅含溶洞;(Ⅱ)含溶洞和裂缝f0;(Ⅲ)含溶洞和裂缝fi(i=0,1,2,3);(Ⅳ)含溶洞和所有裂缝fi(i=0,1,…,7)。对裂缝进行简化处理时,将每条裂缝区域扩展至宽度为0.8 cm的含裂缝多孔介质区域,将真实缝洞型介质和裂缝简化处理后的等效渗透率计算结果进行对比分析,结果见表2。

由表2可知:裂缝简化处理后的计算结果和真实缝洞系统的等效渗透率基本一致,相对误差均低于2%;经过裂缝预处理,求解的网格单元数减少一半,节省了计算量,提高了计算效率;当缝洞在多孔介质内部离散分布时,缝洞型介质的等效渗透率比基岩渗透率略有增加,与基岩渗透率的数量级相同;当缝洞贯穿整个研究区域并相互连通时,缝洞型介质的等效渗透率提高了4个数量级,介质体的渗透性大大改善。

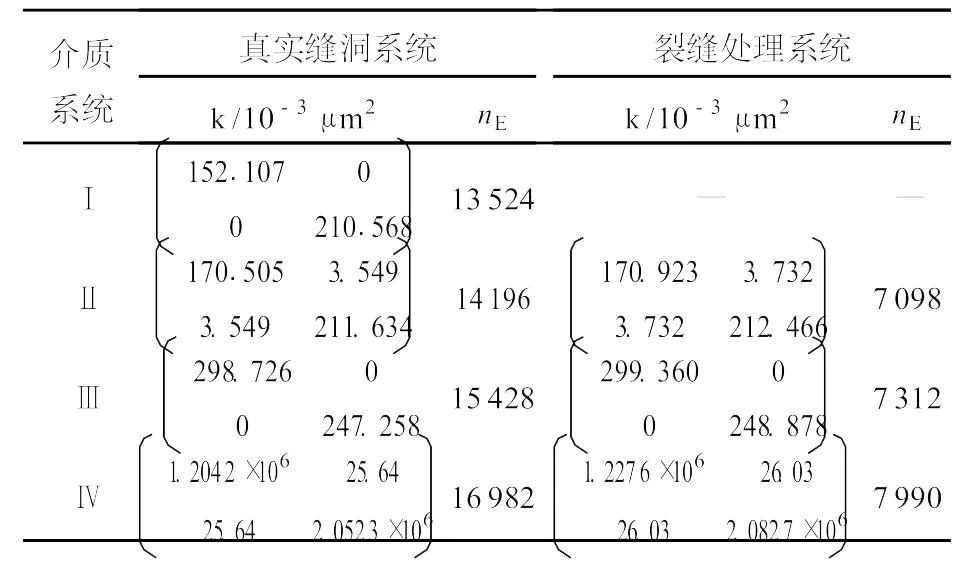
表2 不同介质系统的等效渗透率张量k及网格单元数nE比较Table 2 Comparison of equivalent permeability tensork and grid-element numbernEof different system s

3 结 论

(1)含圆形溶洞介质的等效渗透率与基岩渗透率成线性关系。

(2)缝洞结构的存在会在不同程度上影响介质体的等效渗透率:嵌套于多孔介质内部且边界远离研究区域外边界的缝洞不会显著影响整体的渗透性,其数量级与基岩渗透率相同,且其内部流体可视为等势体;边界靠近研究区域外边界的缝洞以及贯穿整个研究区域并相互连通的缝洞,将会显著提高整体的渗透性,其等效渗透率提高4个数量级。

(3)裂缝预处理技术将溶洞-裂缝-基岩耦合流动问题转化为溶洞-基岩(自由流动和多孔介质渗流)耦合流动问题,能保证计算精度,并且提高了计算效率。

[1] 姚军,王子胜.缝洞型碳酸盐岩油藏试井解释理论与方法[M].东营:中国石油大学出版社,2007.

[2] 张志才,陈喜,石朋,等.喀斯特流域分布式水文模型及植被生态水文效应[J].水科学进展,2009,20(6):806-811.ZHANG Zhi-cai,CHEN Xi,SH IPeng,et al.Distributed hydrological model and eco-hydrological effect of vegetation in Karst watershed[J].Advances inWater Science,2009,20(6):806-811.

[3] 宋付权,许友生,吴锋民.我国生物渗流的研究现状和展望[J].浙江师范大学学报:自然科学版,2007,30(4):372-376.SONG Fu-quan,XU You-sheng,WU Feng-min.Survey and prospect of researches in biological porous flow in China[J].Journal of Zhejiang Normal University(Natural Sciences),2007,30(4):372-376.

[4] HUANG Z,YAO J,L I Y,et al.Per meability analysis of fractured vuggy porous media based on homogenization theory[J].Science China Technological Sciences,2010,53(3):839-847.

[5] SAFFMAN P G.On the boundary condition at the surface of a porous medium[J].Studies in Applied Mathematics,1971,L(2):93-101.

[6] BEAVERS G S,JOSEPH D D.Boundary conditions at a naturally permeable wall[J].Journal of Fluid Mechanics,1967,30:197-207.

[7] SAL INGER A G,AR IS R,DERBY J J.Finite element formulations for large-scale,coupled flows in adjacent porous and open fluid domains[J].Numerical Methods in Fluids,1994,18(2):1185-1209.

[8] GARTL INGD K,H ICKOX C E,G IVLER R C.Simulation of coupled viscous and porous flow problems[J].Computational Fluid Dynamics,1996,7(1):23-48.

[9] ARBOGAST T,BRUNSON D S.A computational method for approximating a Darcy-Stokes system governing a vuggy porous medium[J].Computational Geosciences,2007,11(3):207-218.

[10] KANSCHAT G,R IV IEREB.A strongly conservative finite element method for the coupling of Stokes and Darcy flow[J].Journal of Computational Physics,2010,229(17):5933-5943.

[11] 李亚军,姚军,黄朝琴,等.裂缝性油藏等效渗透率张量计算及表征单元体积研究[J].水动力学研究与进展:A辑,2010,25(1):1-7.L I Ya-jun,YAO Jun,HUANG Zhao-qin.Calculation of equivalent permeability tensor and study on representative element volume for modeling fractured reservoirs[J].Chinese Journal of Hydro-Dynamics(series A),2010,25(1):1-5.

[12] DURLOFSKY L J.Numerical calculation of equivalent grid block per meability tensors for heterogeneous porous media[J].Water Resources Research,1991,27(5):699-708.

[13] 姚军,李亚军,黄朝琴,等.裂缝性油藏等效渗透率张量的边界元求解方法[J].油气地质与采收率,2009,16(6):80-83.YAO Jun,L I Ya-jun,HUANG Zhao-qin,et al.Calculation of equivalent permeability tensors of fractured reservoirs using boundary element method[J].Petroleum Geology and Recovery Efficiency,2009,16(6):80-83.

[14] FENGM,Q IR,ZHU R,et al.Stabilized Crouzeix-Raviart element for the coupled Stokes and Darcy problem[J].Applied Mathematics and Mechanics,2010,31(3):393-404.

(编辑 刘为清)

Estimating equivalent permeability of fractured-vuggy media based on coupled Darcy-Stokes model

L I Ya-jun,YAO Jun,HUANG Zhao-qin,LIU Yong-hui

(College of Petroleum Engineering in China University of Petroleum,Qingdao266555,China)

A coupled Darcy-Stokes model was developed to estimate equivalent permeability(EP)of fractured-vuggy media(FVM)according to the structure property of FVM and the fluid flow characteristics in different-scale voids.The generalized cubic law considering bedrock permeability and equivalent per meability tensor of single-fractured porous media were derived.The pretreatment technique of fractured porous media(FPM)was developed.Thus the vug-fracture-matrix coupled flow problem was converted into the vug-matrix problem.The equivalent permeability and permeability characteristics of different FVMs were analyzed.The results show that the EP of FVM was affected by the existence of fractures and vugs in various degrees.The EP of porous media with single circle vug is linear with the matrix permeability.The pretreatment technique of FPM can enhance the computation efficiency.

fractured-vuggy media;coupled Darcy-Stokes model;continuous media;equivalent permeability;flow simulation

TE 319;TE 344

A

10.3969/j.issn.1673-5005.2011.02.016

2010-11-08

国家科技重大专项(2008ZX05014-005-03);高等学校博士点基金项目(20090133110006);中国石油大学(华东)研究生创新基金项目(Z10-03)

李亚军(1984-),男(汉族),山东费县人,博士研究生,研究方向为油气田开发理论与系统工程。

1673-5005(2011)02-0091-05