基于出砂特征半径的水平井出砂临界生产压差预测模型

尉亚民,王爱萍,董长银,刘春苗

(1.中国石油大学地球资源与信息学院,山东青岛266555;2.青海油田公司钻采工艺研究院,甘肃敦煌736200;3.中国石油大学石油工程学院,山东青岛266555)

基于出砂特征半径的水平井出砂临界生产压差预测模型

尉亚民1,2,王爱萍3,董长银3,刘春苗3

(1.中国石油大学地球资源与信息学院,山东青岛266555;2.青海油田公司钻采工艺研究院,甘肃敦煌736200;3.中国石油大学石油工程学院,山东青岛266555)

在水平井近井地带地应力分布研究基础上,首次提出破坏特征半径的概念,以特征半径处作为地层破坏出砂的判断位置,分别使用Mohr-Coulomb准则、Drucker-Prager准则、Hoek-Brown准则建立相应的水平井出砂临界生产压差预测模型,并对水平井出砂临界生产压差计算结果进行敏感性分析。结果表明:水平井出砂临界生产压差与井斜角有关,其具体变化规律与原始主应力中垂向主应力与最大水平主应力的关系有关;在同一地区,水平井水平段方位的选取会明显影响其生产中的出砂程度;水平井出砂临界生产压差与特征位置半径的选取有直接关系。

水平井;地应力;岀砂预测;出砂临界生产压差;出砂特征半径

水平井出砂预测对于水平井防砂完井方式优选、工作制度优化及开发方案制定都具有重要指导作用,出砂临界生产压差预测是水平井出砂预测的核心内容。油气井出砂的实质是井底流压与流体流动影响近井地应力分布,近井岩石在地应力作用下达到岩石塑性破坏临界条件即岩石破坏准则后,岩石发生塑性破坏,在流体携带作用下造成出砂。目前关于油气井出砂临界生产压差的预测研究主要集中在垂直井中,对于水平井出砂国内外学者通过各种手段进行了初步研究。Abdel-Alim H等[1]根据地应力分布及达西流动分析了裸眼水平井的井壁稳定性,给出了临界流速计算模型;窦宏恩等[2]使用经验定性方法对水平井进行了出砂可能性预测,未涉及临界压差预测;Alireza Nouri等[3]利用有限元方法对水平井出砂进行了模拟,得到一些定性认识;秦积舜等[4]对水平井出砂进行了室内模拟试验,研究了流速等对出砂量的影响;王东辉等[5]以井壁为判断位置对斜井的出砂临界压差进行了研究,建立了初步预测模型。另外也有诸多学者[6-10]对水平井出砂及井壁稳定开展了初步研究。由于水平井井身结构的特殊性以及近井地应力分布复杂,对水平井出砂临界生产压差模型及方法的研究相对较少。笔者在分析水平井近井地带地应力分布基础上,首次提出破坏特征半径的概念,以特征半径处作为地层破坏出砂的判断位置,分别使用Mohr-Coulomb准则、Drucker-Prager准则、Hoek-Brown准则建立相应的水平井出砂临界生产压差预测模型,为水平井出砂预测提供系统的理论与方法。

1 水平井近井地应力分布

出砂是由于地应力突破岩石承受极限而引起的,近井地带应力分布研究是进行出砂预测的基础和条件。由于钻井技术的限制,一般的水平井水平段实际上并非完全水平,而是存在一定的井斜角并且有一定的曲率变化,因此无论是水平井还是大斜度井,实际上都属于斜井的范畴。因此,考虑普遍意义,以斜井为研究对象,其包括了垂直井、水平井、斜井等各种井况。

与垂直井不同,斜井原主地应力方向与井筒轴向不一致,其近井地应力分布比垂直井要复杂得多。需要将地应力分量的表达式进行坐标变换,使之变到与井轴一致的柱坐标系上。以铅垂方向为纵坐标的直角坐标系中,原始地层主应力包括垂向主应力σv、水平最大主应力σH和水平最小主应力σh。为了计算斜井地应力分布,首先要将原始地应力转换到以斜井井轴为纵轴的直角坐标系中,如图1所示。

在以斜井井轴为纵轴的直角坐标系中,原始3个主应力被分解为正应力和剪应力等6个分量,计算公式[6]为

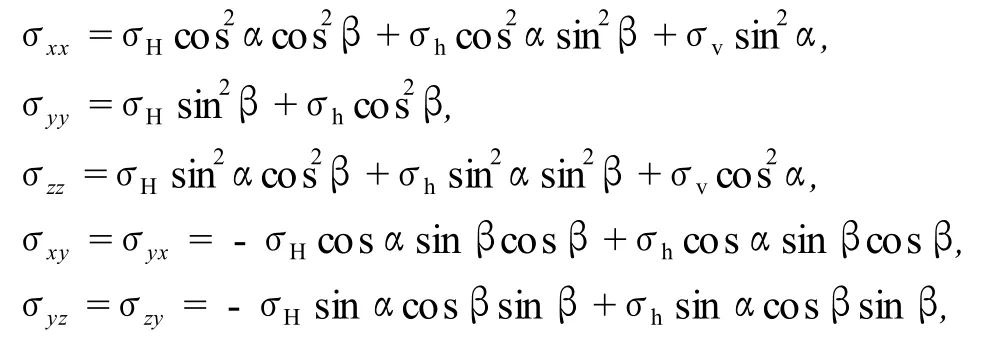
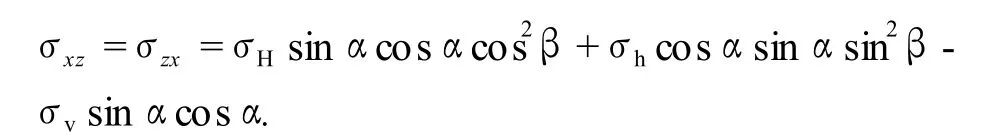
式中,σxx、σyy和σzz为以井轴为纵轴的直角坐标系中的正应力,MPa;σxy、σyz和σzx为剪应力,MPa;α为井斜角,即井轴与铅垂线的夹角,rad;β为井斜方位角,即井斜方位与水平最大主应力方向的夹角,rad。

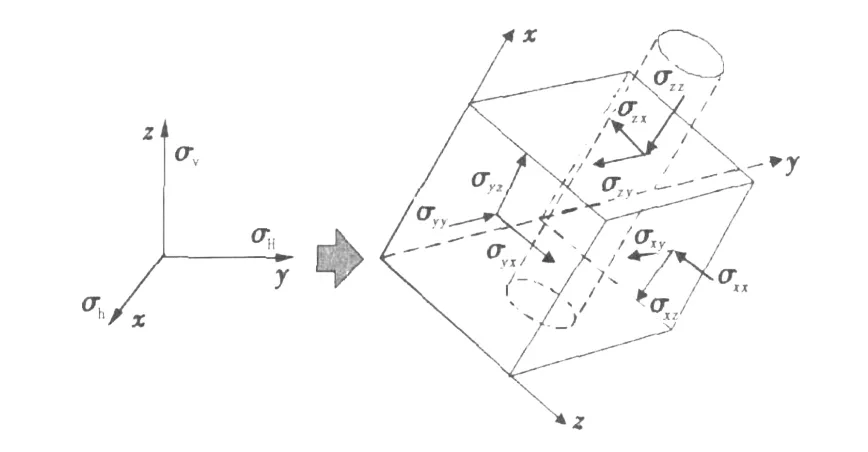
图1 原始地应力坐标变换示意图Fig.1 Sketch map of coordinate transform of original stress

在进行斜井近井带地应力分布研究时,需要建立以斜井井轴为纵轴的柱坐标系,如图2所示。斜井近井地带某一位置的地应力分量包括径向应力σr、切向应力σθ、轴向应力σz以及剪切应力σrθ、σθz、σrz等。

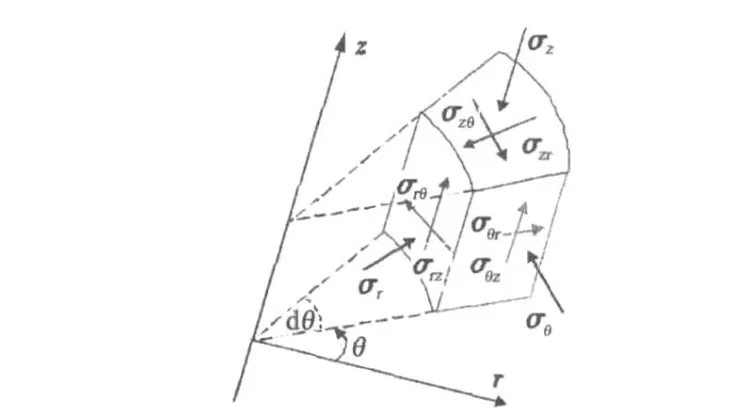
图2 斜井柱坐标系下的近井微元应力示意图Fig.2 Sketch map of infinitesimal stress near wellbore in deviated well cylindrical coordinate system

应用叠加原理得到柱坐标系下各应力分量的表达式为

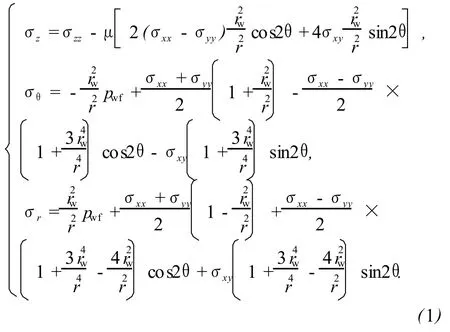
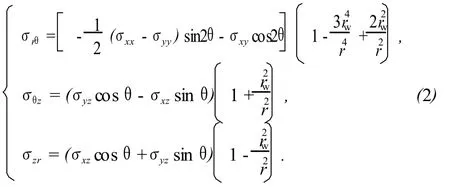
式中,σr、σθ和σz分别为以斜井井轴为纵轴的径向应力、切向应力和轴向应力,MPa;σrθ、σzθ和σrz为柱坐标系下的剪切应力,MPa;rw为井眼半径,m;μ为泊松比;θ为柱坐标系下的圆周角,rad;r为井周某点距井眼轴线的距离,m;pwf为井底流压,MPa。

2 近井岩石破坏出砂特征半径

2.1 出砂特征半径的提出

目前在垂直井出砂临界生产压差模型研究中,通常的方法是根据近井地应力分布求出井壁上(r=rw)的应力[1,5],然后根据岩石破坏准则判断井壁岩石是否破坏,进而求出临界井底流压。其实质是将井壁作为井是否出砂的判别特征位置,也就是说只要井壁上的岩石破坏就意味着井开始出砂。实际上近井一定范围内的岩石发生塑性破坏后才会导致油气井出砂,而仅仅井壁岩石破坏就判定为出砂则比较苛刻,会导致计算得到的临界生产压差偏小。

针对上述问题,提出了出砂特征半径的概念,即将从井壁向地层外延伸某一半径位置(r=rx≥rw)作为判断生产井是否破坏出砂的特征位置(图3),只有当r=rx处的岩石塑性破坏,才认为生产井出砂。以此为标准研究出砂临界生产压差计算模型。出砂特征半径包括了以往取井壁作为特征位置的情况(rx=rw),但更具有普遍意义和灵活性。

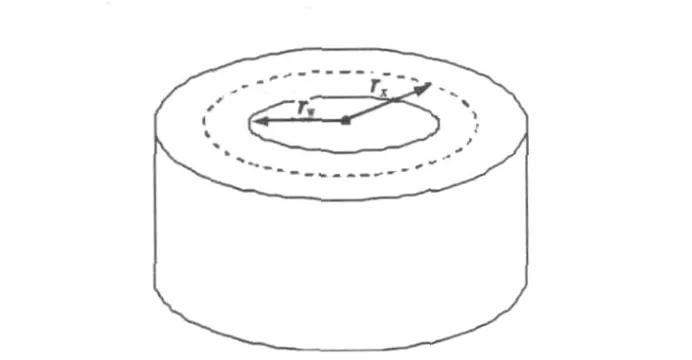
图3 近井岩石破坏出砂特征半径示意图Fig.3 Sketch map of sand inflow characteristic radius for rock damage near well bore

引入出砂特征半径后,斜井的出砂临界生产压差与该特征半径的选取有关。以特征位置r=rx处作为判断位置,则需要根据近井应力分布模型计算得到特征位置处的地应力。

2.2 出砂特征半径rx处的主应力计算

根据式(1)、(2),令r=rx,得到特征位置rx处的各应力分量。井周主应力可由以下矩阵特征值表示:

将矩阵展开得到

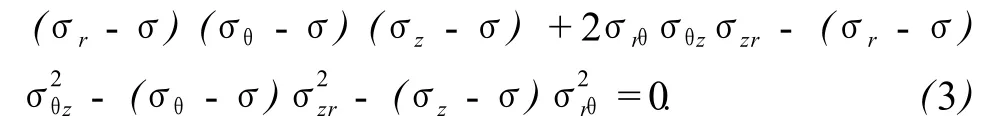
方程(3)为一元三次方程,求解得到其3个根σ′1、σ′2、σ′3,即为3个主应力,表达式为

其中

3 水平井出砂临界压差预测模型

当特征位置rx处的应力达到岩石破坏条件后,岩石发生塑性破坏从而造成出砂。岩石破坏条件即岩石破坏准则。目前油气井出砂预测领域常用的岩石破坏准则有多种,本文中选取常用的Mohr-Coulomb准则、Drucker-Prager准则、Hoek-Brown准则,在分析地应力分布及出砂特征位置定义的基础上,研究出砂临界生产压差预测模型及其计算方法。

3.1 基于M ohr-Coulomb准则

考虑地层岩石孔隙中的流体压力并用主应力表示的Mohr-Coulomb准则[6]为

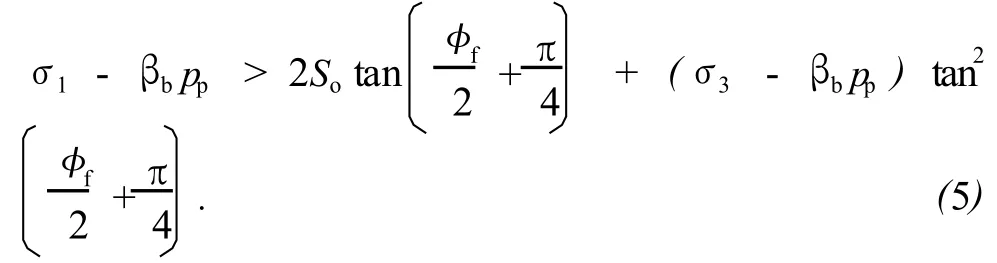
式中,σ1和σ3分别为最大、最小主应力,MPa;βb为Biot弹性系数,;So为岩石内聚强度,MPa;φf为岩石内摩擦角,rad;pp为孔隙压力,MPa。

在特征位置r=rx处,孔隙压力是井底流压pwf的函数,表达式为式中,po为地层静压力,MPa;ro为泄油半径,m。

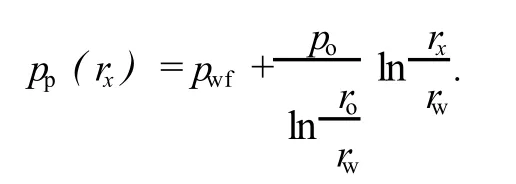
为了求解临界出砂状态条件下的井底流压,假设特征位置rx处正好处于出砂状态,则方程(5)取等式,孔隙压力pp替换为rx处的值,得到

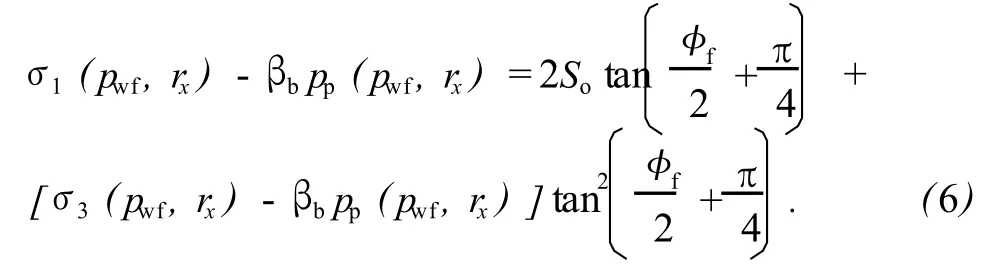
其中主应力σ1和σ3分别为根据方程(4)计算得到的3个主应力分量中的最大和最小主应力,即

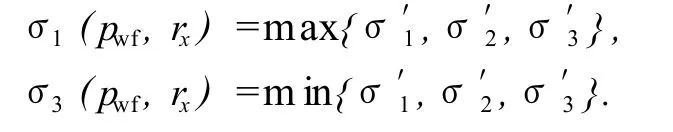
方程(6)是一个关于井底流压pwf的等式,将pwf视为未知数据,求解得到其值,即特征位置rx处的出砂临界井底流压,已知地层静压后可计算得到出砂临界生产压差。

3.2 基于Drucker-Prager准则

Drucker-Prager准则[6]认为当达到如下条件时岩石发生破坏:

其中

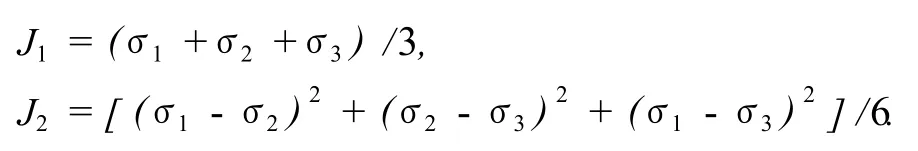
式中,J1和J2分别为第一、第二偏应力不变量;C0和C1为岩石强度参数,通过岩石力学试验得到。

特征位置rx处临界出砂状态下,方程(7)取等式,主应力σ1、σ2、σ3分别为

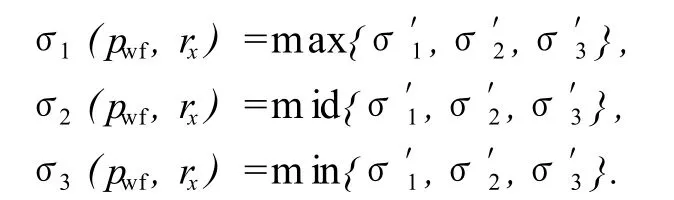
将其代入方程(7)得

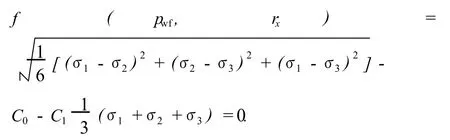
3.3 基于Hoek-Brown准则

Hoek和Brown基于岩石抛物线型破坏包络线的系统研究,提出了岩石破坏经验准则[6],即

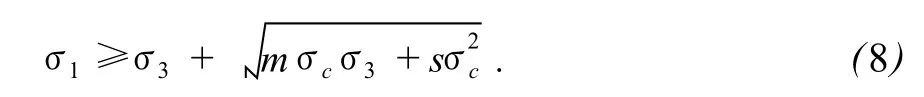
式中,σc为岩石单轴抗压强度,MPa;m和s为经验系数。

特征位置rx处临界出砂状态下,方程(8)取等式,得

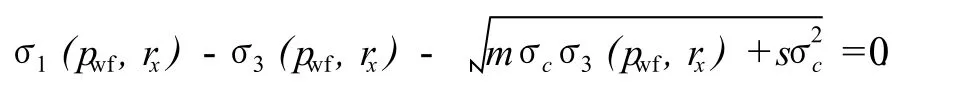
需要注意的是,由于在特征位置rx处,不同的圆周角θ处地应力不相同并呈周期性变化,因此利用上述模型计算出砂临界生产压差时,需要首先给定一个圆周角θ,即在特征位置rx处计算得到出砂临界生产压差随圆周角θ的变化。

4 实例计算及敏感性分析

某水平井地层静压11.18 MPa,井眼半径为0.125 m,水平段深度1.038 km,方位角285.3°,井斜角89°;原始垂向主应力为22.05 MPa,最大、最小水平主应力分别为29.38和21.43 MPa,水平最大主应力方位角为128.26°,地层岩石泊松比为0.38,岩石内聚力7.34 MPa,内摩擦角25.25°,单轴抗压强度为30.05 MPa;Hoek-Brown准则中的系数分别取m=1.5,s=0.004;Drucker-Prager准则岩石强度参数分别取C0=7.43 MPa,C1=0.19。使用上述数据对该井出砂临界生产压差进行计算分析。

4.1 计算结果

以井轴为纵坐标的直角坐标系下的正应力与剪应力为σxx=22.05 MPa,σyy=22.64 MPa,σzz=28.17 MPa,σxy=0.05MPa,σyz=0.11MPa,σzx=2.86MPa。

选取出砂特征半径rx=0.15 m,使用应力模型得到特征位置处各主应力随圆周角和半径的变化曲线如图4所示。靠近井壁处,应力与原始地应力相差较大,越向外围越趋向于原始地应力。

该井实际出砂监测统计值为出砂临界井底流压9.0 MPa,临界生产压差2.18 MPa。根据上述给定基础数据,分别使用3种岩石破坏准则得到的该井出砂临界生产压差结果见表1。

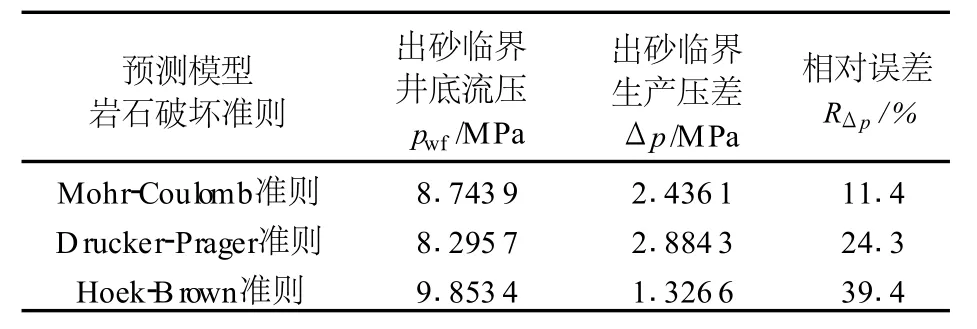
表1 出砂临界生产压差计算结果对比Table 1 Comparison of calculated results of critical producing pressure difference of sand inflow

基于3种岩石破坏准则得到的结果相差较大,其中Mohr-Coulomb准则得到的结果与实际出砂监测资料最接近,误差为11.4%。此结果仅为该单井分析结果,其是否具有代表性有待深入研究。

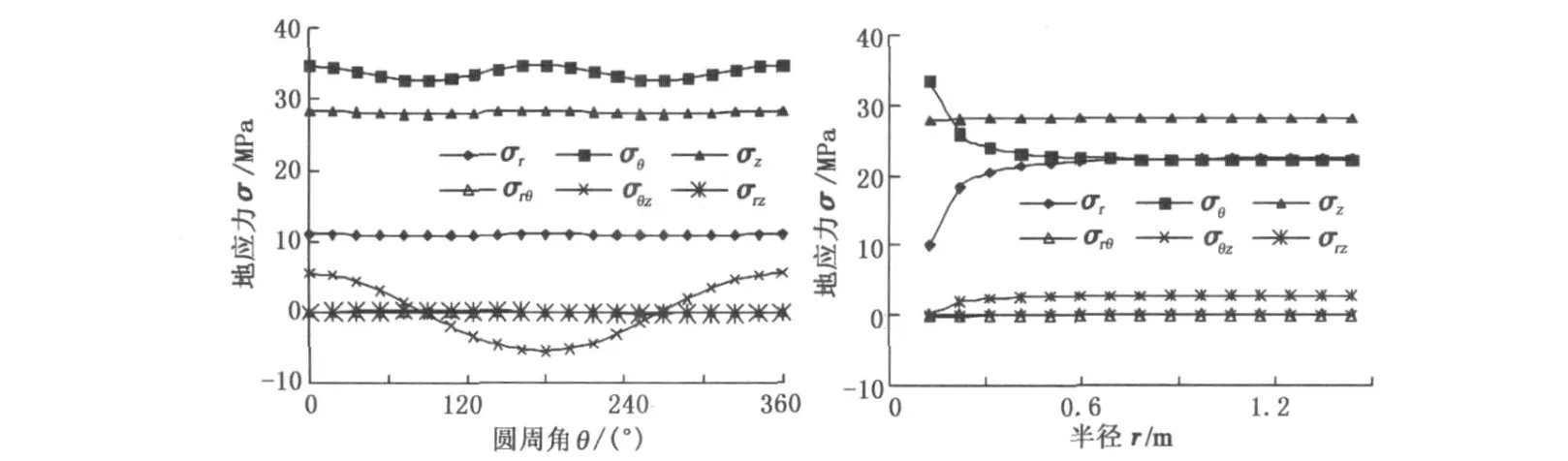
图4 近井地带地应力随圆周角和半径位置的变化Fig.4 Change of stress near wellbore with circumferential angle and radius site

4.2 出砂临界生产压差影响因素

4.2.1 井斜角

只改变水平段井斜角,计算得到水平井出砂临界生产压差随井斜角的变化如图5所示。σv＜σH时,随着井斜角的增大(即井筒趋于水平),出砂临界生产压差逐渐增大,地层越不容易出砂;σv＞σH时与σH＞σv情况下得到变化规律正好相反。因此,水平井出砂临界生产压差与井斜角有关,其具体变化规律与原始主应力中垂向主应力与最大水平主应力的相互关系有关。

4.2.2 方位角

只改变水平井水平段的方位角,计算得到水平井出砂临界生产压差随水平井方位角的变化如图6所示。水平井出砂临界生产压差随方位角呈周期性变化。这说明,在同一地区或地层,水平井水平段方位的选取会明显影响其生产中的出砂程度。该结果对于水平井井位及井深结构设计具有重要指导作用。

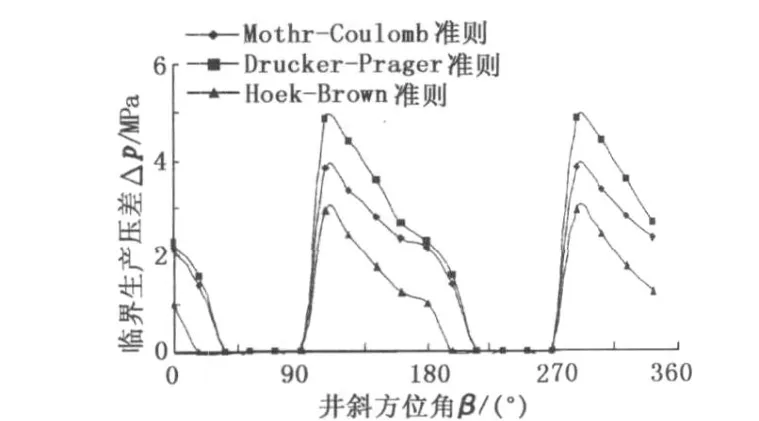
图6 临界生产压差随井斜方位角的变化曲线Fig.6 Change of critical producing pressure difference with drift az imuth

4.2.3 特征位置

计算得到的出砂临界生产压差随出砂特征半径rx的变化如图7所示。水平井出砂临界生产压差与特征位置半径的选取有直接关系。特征半径越大,得到的临界生产压差越大。以往在垂直井出砂预测研究中,实质以井壁作为特征位置的作法得到临界生产压差值属于最小值,比合理值要偏小。

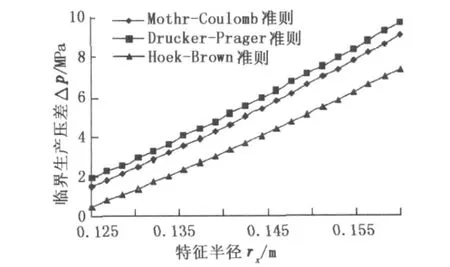
图7 临界生产压差随特征半径的变化曲线Fig.7 Change of critical producing pressure difference with characteristic radius

4.2.4 岩石内聚力与内摩擦角

目前,最常用的岩石破坏准则是Mohr-Coulomb准则,其中使用的岩石内聚力和内摩擦角是地层岩石的两个基本强度参数。图8为使用Mohr-Coulomb准则计算得到的水平井出砂临界生产压差随岩石内聚力和内摩擦角的变化曲线。随着岩石内聚力和内摩擦角的增加,水平井出砂临界生产压差增大,即生产井越不容易出砂。

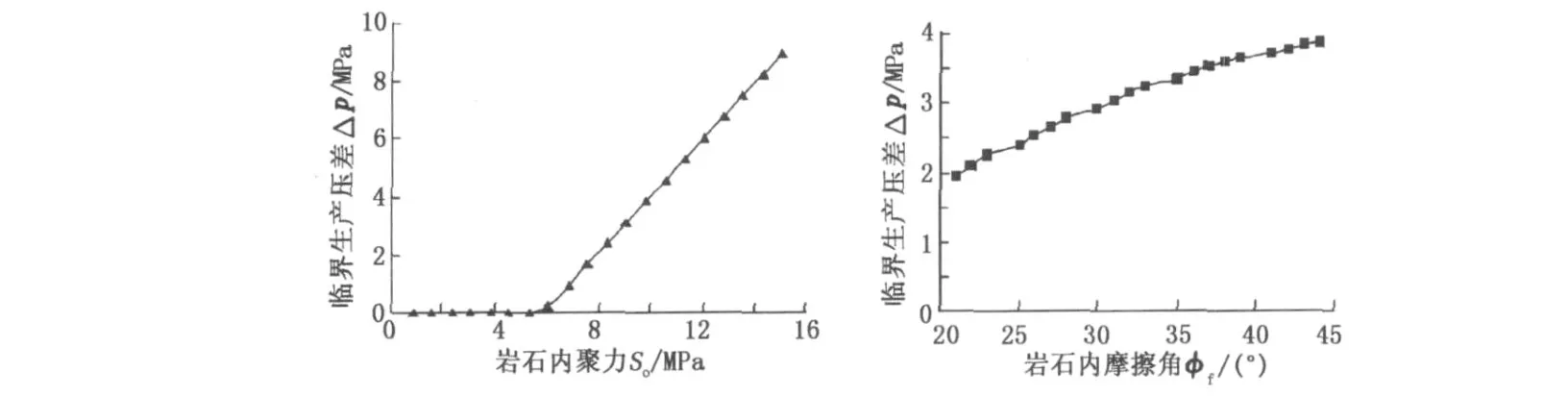
图8 临界压差随岩石内聚力和岩石内摩擦角的变化Fig.8 Change of critical producing pressure difference with rock cohesive force and inner friction angle

5 结 论

(1)以特征半径处作为地层破坏出砂的判断位置,分别使用Mohr-Coulomb准则、Drucker-Prager准则、Hoek-Brown准则建立的水平井出砂临界生产压差预测模型适用于斜井、水平井等各种情况。

(2)水平井出砂临界生产压差与井斜角有关,其具体变化规律与原始主应力中垂向主应力与最大水平主应力的相互关系有关。在原始水平最大主应力大于垂向主应力的条件下,随着井斜角的增大(即井筒趋于水平),出砂临界生产压差逐渐增大,地层越不易出砂;当原始水平最大主应力小于垂向主应力时,其变化趋势正好相反。

(3)水平井出砂临界生产压差随方位角呈周期性变化。在同一地区或地层,水平井水平段方位的选取会明显影响其生产中的出砂程度。

(4)水平井出砂临界生产压差与特征位置半径的选取有直接关系。特征半径越大,得到的临界生产压差越大。以往以井壁作为特征位置的作法得到的临界生产压差属于最小值,比合理值要偏小。

[1] ABDEL-AL IM H,ALSUGHAYER AliA.A new concept to predict sand production from extended reach and horizontal wells[R].SPE 68134,2001.

[2] HONGEN D,DANDAN H,WENX IN C.Sand production prediction and the selection of completion methods for horizontal well in Intercampo Oilfield,Venezuela[R].SPE 93821,2005.

[3] AL IREZA Nouri,HANS Vaziri.Comprehensive transient modeling of sand production in horizontal wellbores[R].SPE 84500,2007.

[4] 秦积舜,王作颍.水平井出砂模拟试验研究[J].石油钻探技术,2000,28(4):34-36.Q IN Ji-shun,WANG Zuo-ying.Exper imental study on sand production in horizontal well[J].Petroleum Drilling Techniques,2000,28(4):34-36.

[5] 王东辉,韩英,高娟,等.斜井临界生产压差预测[J].断块油气田,2008,15(6):102-104.WANG Dong-hui,HAN Ying,GAO Juan,et al.Prediction of critical drawdown pressure for inclined well[J].Fault-Block Oil&Gas Field,2008,15(6):102-104.

[6] 楼一珊,金业权.岩石力学与石油工程[M].北京:石油工业出版社,2006.

[7] 王艳辉,刘希圣.定向油气井出砂模型的建立与参数分析[J].石油大学学报:自然科学版,1995,19(增刊):60-65.WANG Yan-hui,LIU Xi-sheng.Analysis on stress distribution in directional well and factors affecting on sand production[J].Journal of the University of Petroleum,China(Edition of Natural Science),1995,19(sup):60-65.

[8] 金衍,陈勉,柳贡慧.弱面地层斜井井壁稳定性分析[J].石油大学学报:自然科学版,1999,23(4):33-35.J IN Yan,CHEN Mian,LIU Gong-hui.Analysis on borehole stability of weak-face for mation in directional wells[J].Journal of the University of Petroleum,China(Edition of Natural Science),1999,23(4):33-35.

[9] 刘洪,刘向君,孙万里,等.水平井眼轨迹对气井出砂趋势及工作制度的影响[J].天然气工业,2006,26(12):103-105.L IU Hong,L IU Xiang-jun,SUN Wan-li,et al.How horizontal well trajectory affects the sand-producing tendency and working system of a gas well[J].Natural Gas Industry,2006,26(12):103-105.

[10] 张文波,周鹏高,李亚双,等.不同地应力场对大斜度井井壁稳定规律的影响[J].天然气技术,2010,4(1):58-60.ZHANG Wen-bo,ZHOU Peng-gao,L I Ya-shuang,et al.Effect of borehole stability in highly deviated wells under different in-situ stress fields[J].Natural Gas Technology,2010,4(1):58-60.

(编辑 李志芬)

Prediction model for critical sanding pressure drawdown in horizontal wells based on characteristic break radius

WEI Ya-min1,2,WANG Ai-ping3,DONG Chang-yin3,LIU Chun-miao3

(1.College of Geo-Resources and Information in China University of Petroleum,Qingdao266555,China;2.Research Institute of D rilling and Production,Qinghai Oilfield,Dunhuang736200, China;3.College of Petroleum Engineering in China University of Petroleum,Qingdao266555,China)

Based on the for mation stress distribution model around horizontal well bore,the concept of characteristic break radius was put forward firstly and used as the evaluation location to judge whether the well sanding or not.Three rock failure criterions,which concerns Mohr-Coulomb,Drucker-Prager and Hoek-Brown,were applied to develop the critical downhole pressure condition,and the corresponding critical sanding pressure drawdown prediction models were established.The model was used to analyze the effect of production parameters and rock characteristic on the critical sanding pres sure drawdown.The results indicate that the critical sanding pressure drawdown is related to the hole angle,but the varying tendency depends on the relationship of initial formation vertical stress and maximum horizontal stress.In the same reservoir,the well orientation angle affects the sand production degree directly.In addition,the critical sanding pressure drawdown changes with the characteristic break radius obviously.

horizontalwell;stress distribution;sanding prediction;critical sanding pressure drawdown;characteristic break radius

TE 257

A

10.3969/j.issn.1673-5005.2011.02.015

2010-05-05

国家自然科学基金项目(50704035);国家“863”计划项目(2006AA09Z351)

尉亚民(1963-),男(汉族),山西襄汾人,高级工程师,博士研究生,从事石油地质、水平井开发等方面的研究工作。

1673-5005(2011)02-0085-06