射流冲击载荷对井底岩石应力场的影响

常德玉,李根生,沈忠厚,黄中伟,田守嶒,史怀忠,宋先知

(中国石油大学油气资源与探测国家重点实验室,北京102249)

射流冲击载荷对井底岩石应力场的影响

常德玉,李根生,沈忠厚,黄中伟,田守嶒,史怀忠,宋先知

(中国石油大学油气资源与探测国家重点实验室,北京102249)

考虑三向地应力、液柱压力、孔隙压力和射流速度的影响,建立射流冲击井底岩石流固耦合模型,运用有限元及有限体积法进行求解。结果表明:井底压差越大,井底岩石最大主应力越大;射流最大冲击压力与速度平方成正比,孔隙压力在冲击面和冲击轴线上随距离增加均呈“三次抛物线”减小;射流冲击井底岩石存在明显的局部效应,射流主要影响区域在冲击面上约为2倍射流半径,在冲击轴线上约为2.5～3.5倍射流半径,与应力波理论结果相吻合。

射流;井底岩石;流固耦合;应力场;有限元法;有限体积

石油钻井过程中钻头喷嘴射流的冲击作用能够直接或辅助破岩钻孔,并且井底流体有利于清离井底岩屑,从而提高机械钻速[1]。国内外学者已在射流破岩机制研究方面做了大量工作:目前比较公认的主要有拉伸-水楔破岩理论和密实核-劈拉破岩理论[2];射流冲击岩石时应力波破岩为主要作用,准静态压力作用为其次[3];通过试验研究得出射流破岩存在门限压力和最优喷距,射流压力越大,破岩效果越好[4],围压越大,破岩效果越差[5-6];数值模拟研究得出射流存在等速核,射流冲击时岩石表面为拉伸破坏,内部为剪切破坏[7-8],将射流冲击岩石简化为刚性接触体与岩石接触进行分析,通过研究得出射流冲击破岩发生时间约毫秒级且存在两个门限压力[9-10]。在钻井过程中,射流破岩属于流固耦合问题,机制十分复杂,一方面井眼的形成属于“端面开挖效应”,目前此类问题尚无解析解[11],另一方面井底岩石受三向地应力、液柱压力、孔隙压力、射流冲击力和机械载荷的作用,同时考虑这些因素时试验研究难以实现。笔者采用数值模拟方法,考虑三向地应力、液柱压力、孔隙压力和射流冲击力等因素的影响建立流固耦合模型,对不同射流速度冲击时岩石内部孔隙压力分布和不同射流速度对井底岩石应力场的影响进行研究。

1 控制方程

1.1 岩石控制方程

井底岩石的平衡方程、几何方程和物理方程[12]为

岩石骨架应力由有效应力原理表示为

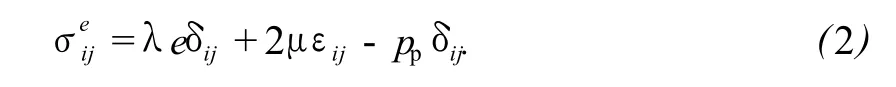
其中

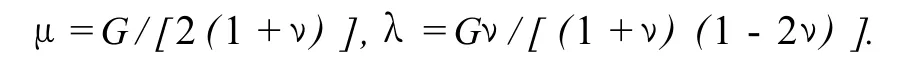
式中,Fi为体积力,N;e为体积应变;pp为孔隙压力,MPa;εij为弹性应变分量;σij为总应力,MPa;为骨架应力,MPa;ν为泊松比;G为刚度模量;MPa;i=j时,δij=1,i≠j时,δij=0。

1.2 流体控制方程

1.2.1 环空流体控制方程

流体质量守恒、动量守恒和能量守恒方程[13]为

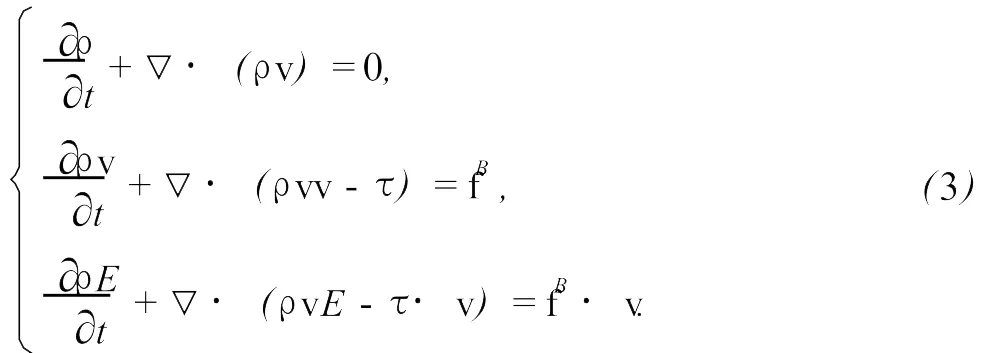
式中,t为时间,s;ρ为流体密度,g/cm3;v为速度矢量;fB为体积力矢量;τ为应力张量;E为比动能。

1.2.2 渗流方程

当液柱压力与孔隙压力存在压差时,地层中的孔隙压力发生变化,使岩石骨架应力重新分布。地层中的流体流动满足达西渗流定律,流体流动控制方程[14]为

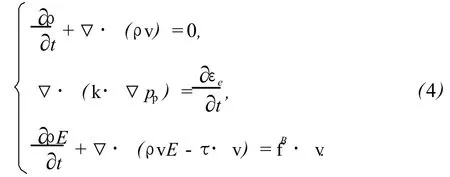
式中,k为渗透率张量,μm2;εe为孔隙骨架的体积应变。

2 射流冲击岩石物理模型

假设:岩石各向同性且孔隙内部充满流体;渗流为稳定达西渗流;不考虑边界层和液体的压缩性;射流喷距在等速核范围内;不考虑井斜、裂缝和温度等其他因素的影响。

由于实际井壁和井底形状十分复杂,为了描述出其几何和力学特征,取井底面为平面,井壁面为光滑壁面,射流冲击井底岩石物理模型如图1所示。

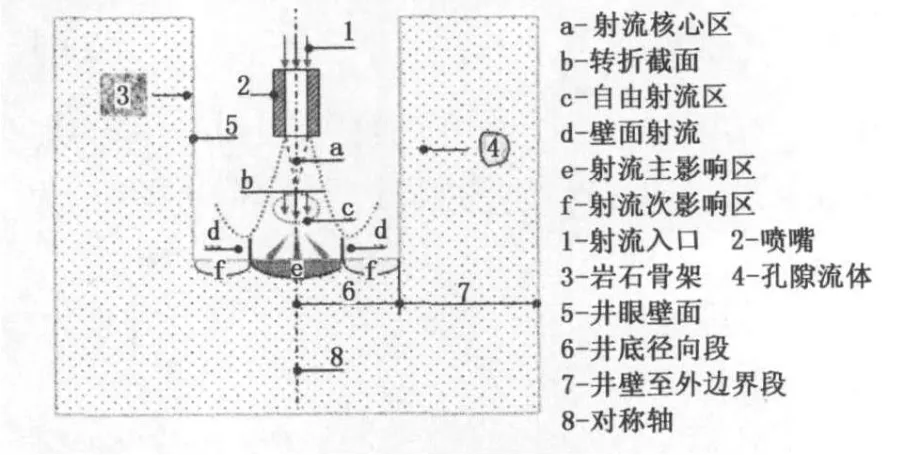
图1 射流冲击井底岩石物理模型Fig.1 Physicalmodel of bottom-hole rock under water jet impact

模型参数:①井眼参数为井深3 km,井眼直径300 mm,为了减小井眼尺寸的局部影响,模型外边界取10倍井眼直径,井壁为规则圆柱面,井底面为规则平面;②材料参数为岩石密度2 500 kg/m3,孔隙度10%,渗透率0.1μm2;流体密度1 000 kg/m3,动力黏度0.01 Pa·s;③射流参数为喷嘴直径2 mm,喷距在等速核范围内,流体采用标准k-ε模型,c1=1.44,c2=1.92,cμ=0.09,σk=1.0,σε=1.3,射流速度取50、100、150、200和250 m/s;④地应力参数为上覆岩层压力75 MPa,最大和最小水平地应力分别取60和50MPa,孔隙压力30MPa,液柱压力取26、28、30、32和34 MPa。模拟欠平衡、平衡和过平衡3种钻井方式不同射流速度下的井底岩石应力场。

3 射流冲击岩石耦合分析

岩石属于多孔介质,因此在射流冲击岩石表面后,在岩石内部一定范围内孔隙压力将产生较大变化。射流冲击岩石包括射流与岩石骨架、孔隙流体与岩石骨架、射流与孔隙流体耦合。

(1)射流和孔隙流体耦合。射流冲击时在冲击区域范围内使得岩石内部孔隙压力改变,根据达西渗流定律,可简化为球形区域的中心向外渗流的情况。由于岩石的渗透率较低,此时渗流速度较小,但此压力波的传播速度量级为km/s,因此在很短的时间内就可以将此压力传播到地层较远处,使得岩石中一定区域内的孔隙压力迅速增大。单相液体球面模型向外渗流微分方程用极坐标[15]表示为

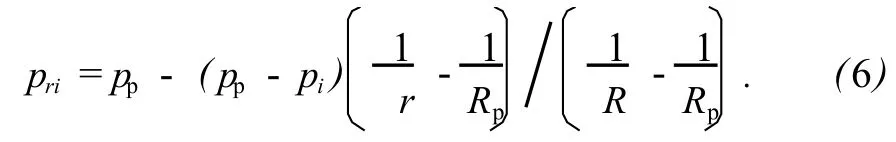
式中,pri为射流冲击区域内孔隙压力,MPa;pi为射流冲击压力,MPa;Rp为模型外边界半径,m;R(i)为射流冲击半径,m。

(2)孔隙流体和岩石骨架耦合。其耦合方程为

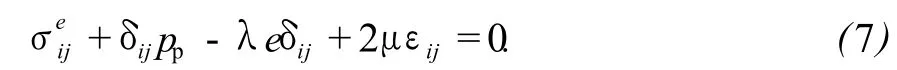
(3)射流与岩石骨架耦合。射流与岩石骨架耦合首先发生在射流与岩石的交界面上,在交界面上应满足位移和应力协调条件,即

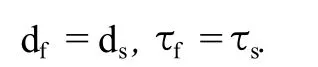
式中,df为流体位移;ds为固体位移;τf为流体应力;τs为固体应力。

4 射流冲击岩石模型求解

4.1 固体模型

单元类型为三维20节点六面体单元,模型共划分22400个单元,单元节点的形状函数[16]为

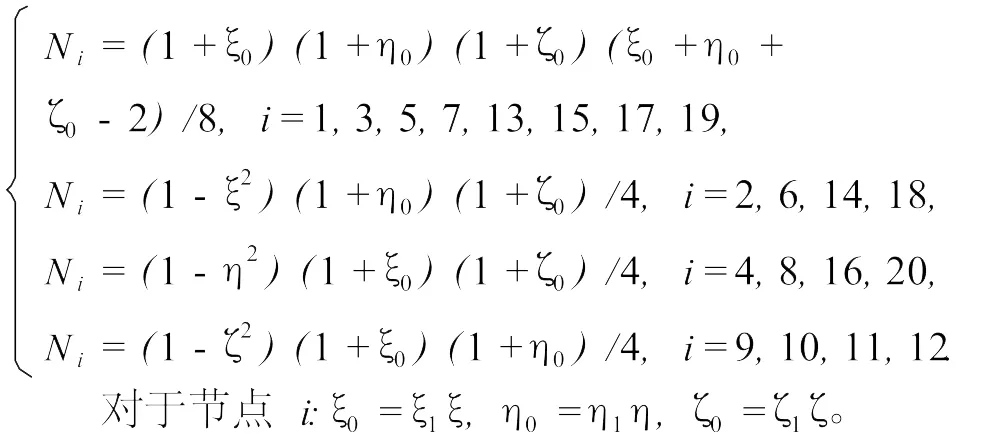
采用有限元方法进行计算,有限元求解方程为

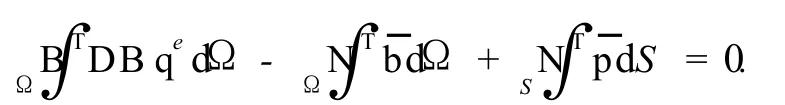
其中

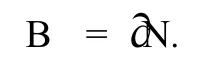
4.2 流体模型

单元类型为三维8节点六面体单元,模型共划分60000个单元。环空流体和渗流模型按照有限体积法进行计算,环空流体方程的积分形式为

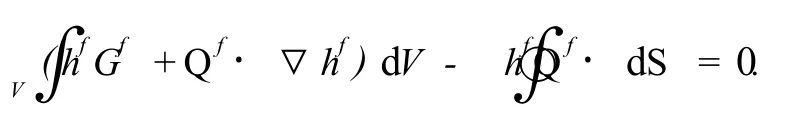
式中,f为连续性方程、动量方程和能量方程中的p,v和θ;hf为阶跃函数。

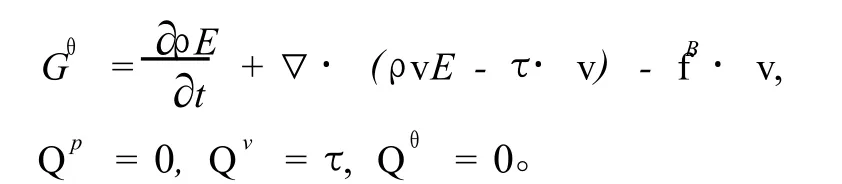
岩石内部流体与环空流体的连续性方程和能量方程相同,动量方程的保守积分形式为

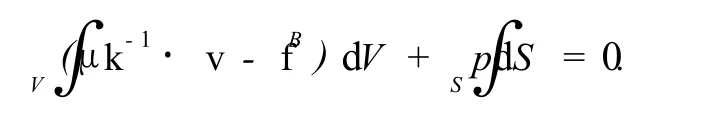
4.3 边界条件

应力边界条件:模型施加上覆岩层压力为75 MPa,孔隙压力为30 MPa,水平最大和最小总地应力分别为60和50 MPa。

位移边界条件:模型底部施加法向约束,喷嘴内部施加无滑移边界条件。

速度入口条件:在喷嘴处施加速度载荷。

压力出口条件:围压为液柱压力。

4.4 计算步骤

耦合系统的解向量为X=(Xf,Xs),Xf和Xs分别为流体和固体节点上的解向量;ds=ds(Xs),τf=τf(Xf)。Ff和Fs为流体方程和固体方程相对应的求解方程,当固体位移为0时,流体求解方程Ff[Xf,0]=0;当流体边界力为0时,固体求解方程Fs[Xs,0]=0。

5 结果分析

井位确定后,钻井过程中某一层位的地层岩性、三向地应力状态、孔隙压力等参数数值基本确定,因此影响岩石破碎的外界因素主要有钻头载荷、射流载荷和井底压差等因素。

5.1 射流冲击下孔隙压力分布规律

5.1.1 冲击面上孔隙压力分布

为了研究射流冲击对岩石孔隙压力的影响,取过平衡钻井状态进行分析,井底压差取4 MPa,结果如图2所示。射流冲击时冲击面上岩石孔隙压力在径向距离0～20 mm内随径向距离的增加呈“倒三次抛物线”迅速减小,射流冲击速度越大,冲击面上孔隙压力衰减越快;径向距离大于20 mm后孔隙压力逐渐趋于稳定值34 MPa;射流冲击速度从50 m/s增大至250 m/s时,冲击面上最大孔隙压力从35.25 MPa增大至65.25 MPa。

将冲击面上孔隙压力数值进行回归分析,得出冲击面上孔隙压力分布规律为pp=Ax3+B x2+Cx+D,回归系数见表1。

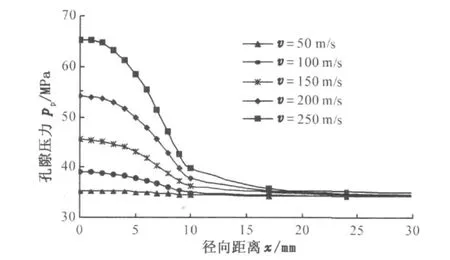
图2 冲击面上孔隙压力分布Fig.2 D istribution of pore pressure on impact surface

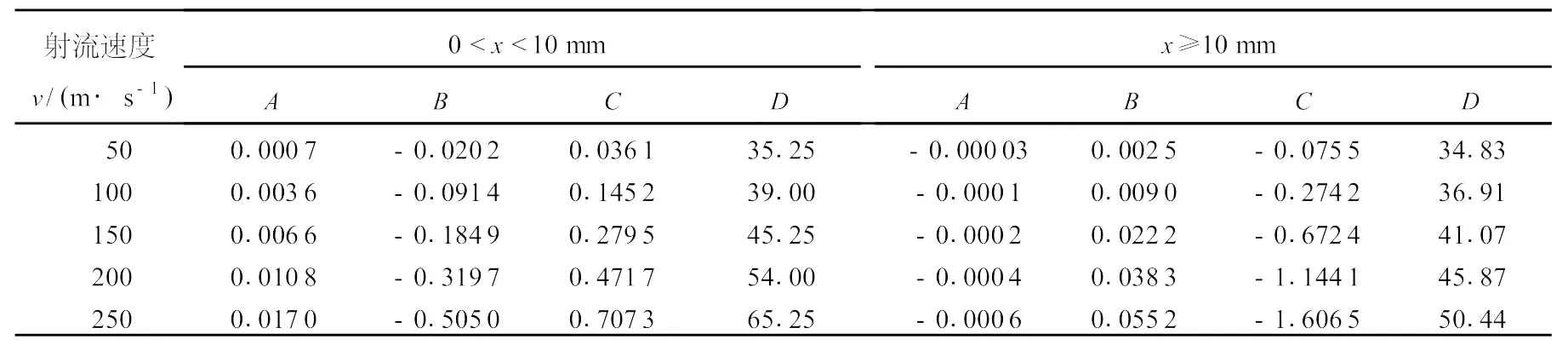
表1 冲击面上孔隙压力回归分析系数Table 1 Regressive analysis coefficients of pore pressure on impact surface

5.1.2 冲击轴线上孔隙压力分布

如图3所示:射流冲击时冲击轴线上孔隙压力在轴向距离0～40 mm内随轴向距离增加呈“正三次抛物线”迅速减小,射流冲击速度越大冲击轴线上孔隙压力衰减越快;轴线距离大于40 mm时逐渐减小且不同射流速度时其减小规律基本一致。射流冲击时冲击压力在岩石孔隙内部通过流体进行传播,且流体只能传播纵波,由于岩石的渗透率较小,因此在射流冲击压力传播时波阻抗较大。

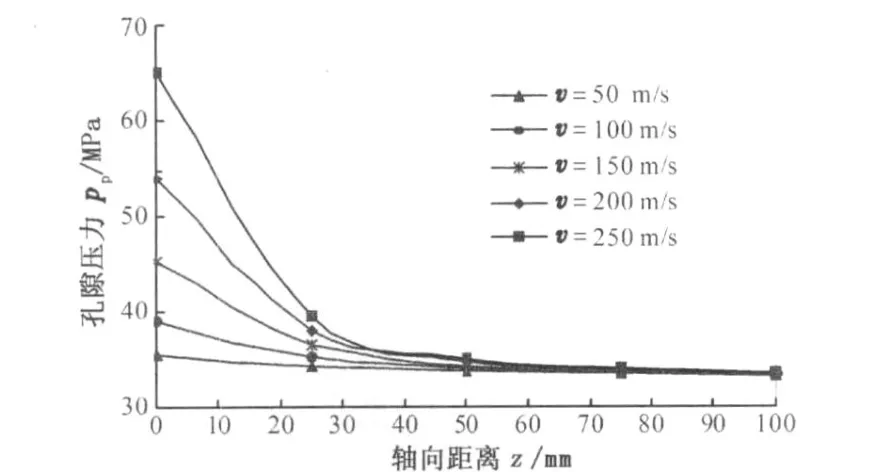
图3 冲击轴线上孔隙压力分布Fig.3 D istribution of pore pressure along impact axis

将冲击轴线上孔隙压力数值进行回归分析,得出射流冲击轴线上孔隙压力分布规律为pp=az3+bz2+cz+d,回归系数见表2。此分布规律与文献[17]和[18]中应力波衰减规律相似,验证了结果的正确性。

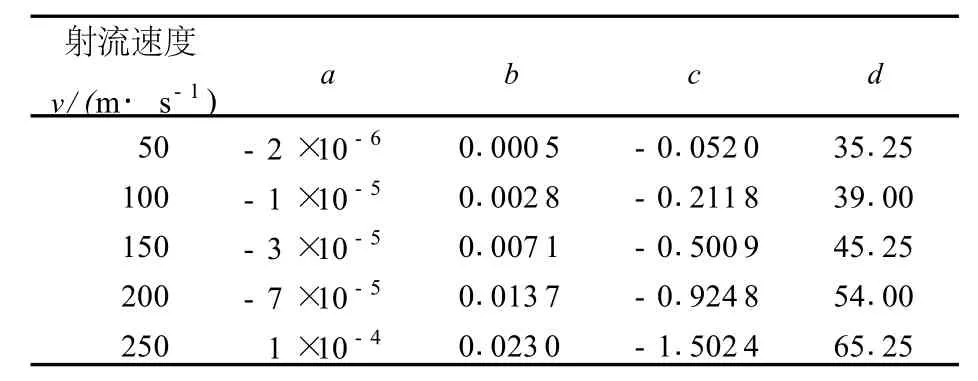
表2 冲击轴线上孔隙压力回归分析系数Table 2 Regressive analysis coefficients of pore pressure along impact axis

5.2 射流冲击下井底岩石应力场分布规律

由于岩石的抗拉强度小于抗剪和抗压强度,射流冲击岩石时射流速度越大,岩石内部孔隙压力增加越明显,当孔隙压力增加到一定值时,岩石受拉载荷超过抗拉强度而产生拉伸破坏。因此,射流冲击作用下岩石应力场中主要针对岩石的最大主应力进行分析。

5.2.1 井底压差的影响

射流速度取100 m/s,将井底面最大主应力沿径向距离分布和井眼轴线最大主应力沿轴向距离分布进行对比分析,结果见图4。不同井底压差时井底面最大主应力为压应力且沿径向距离分布规律相似。当径向距离为0～20 mm时,随径向距离增加最大主应力减小较快,当径向距离大于20 mm时,随径向距离增加最大主应力缓慢减小;在同一径向距离处,当井底压差从4 MPa减小至-4 MPa时,其对应的最大主应力呈均匀梯度减小。不同井底压差下井眼轴线最大主应力分布规律也相似。随着轴向距离的增加,井眼轴线最大主应力逐渐由拉应力转变为压应力,当轴向距离为0～25 mm时,约呈线性减小为0 MPa,且井底压差从4 MPa减小至-4 MPa时,最大主应力逐渐减小;当轴向距离大于25 mm时井眼轴线最大主应力也呈线性减小,且不同井底压差下变化幅度基本相同。

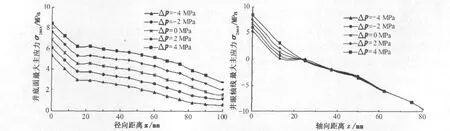
图4 不同井底压差下井底面和井眼轴线最大主应力分布Fig.4 D istribution of the greatest principal stress in bottom-hole surface and wellbore axis with different bottom-hole pressure difference

5.2.2 射流速度的影响

井底压差取4 MPa,将井底面和井眼轴线最大主应力进行对比分析,结果见图5。不同射流冲击速度下井底面最大主应力均为拉应力且沿径向距离分布规律相似。当径向距离为0～20 mm时,随径向距离增加,最大主应力迅速减小,射流冲击速度越大最大主应力数值越大且减小速度越快;当径向距离大于20 mm时,随径向距离增加,最大主应力呈线性缓慢减小,同一井底面位置处不同射流速度冲击下井底面最大主应力基本保持不变。不同射流冲击速度下井眼轴线最大主应力均沿轴向距离由拉应力转变为压应力且分布规律也相似。当轴向距离为0～25 mm时,不同射流速度冲击下井眼轴线最大主应力均为拉应力,射流速度从50增大至250 m/s时井眼轴线受拉深度由25 mm增大至35 mm,射流速度越大,井眼轴线最大主应力数值越大,且沿轴向减小速度越快;当垂向距离大于35 mm时,随轴向距离增加,最大主应力逐渐减小,同一井眼轴线处不同射流速度冲击下井眼轴线最大主应力基本保持不变。

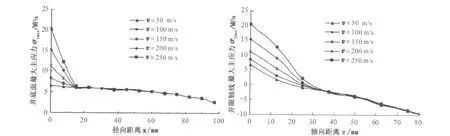
图5 不同射流速度下井底面和井眼轴线最大主应力分布Fig.5 Distribution of the greatest principal stress in bottom-hole surface and wellbore axis with different jet velocity

6 结 论

(1)射流冲击井底岩石应力场存在射流与岩石骨架耦合、孔隙流体与岩石骨架耦合和射流与孔隙流体耦合3种耦合作用。

(2)井底压差一定,当径向距离小于10 mm时,不同射流速度下射流冲击面上孔隙压力均呈“倒三次抛物线”迅速减小,当径向距离大于10 mm时,呈“正三次抛物线”缓慢减小;不同射流速度下冲击轴线上孔隙压力均呈“正三次抛物线”迅速减小;井底面最大主应力随径向距离增加在2倍射流半径内迅速减小,大于2倍射流半径时缓慢减小且与射流速度基本无关;冲击轴线最大主应力随轴向距离增加在2.5～3.5倍射流半径内迅速减小,当大于3.5倍射流半径时,随轴向距离增加趋于缓慢减小且与射流速度基本无关。

(3)射流速度一定时,井底压差越大,井底面最大主应力越大;井底面最大主应力随径向距离增加,在2倍射流半径内为拉应力且迅速减小然后趋于缓慢减小;冲击轴线上最大主应力在2.5倍射流半径内为拉应力且随压差增大而增大,当大于2.5倍射流半径时,最大主应力转变为压应力且与压差基本无关。

[1] 沈忠厚.水射流理论与技术[M].东营:石油大学出版社,1998.

[2] 王瑞和,倪洪坚.高压水射流破岩钻孔过程的理论研究[J].石油大学学报:自然科学版,2003,27(4):44-47.WANG Rui-he,N I Hong-jian.Theoretical study on rock break-off process during high-pressure water jet drilling[J].Journal of the University of Petroleum,China(Edition ofNatural Science),2003,27(4):44-47.

[3] DAN IEL L M.Experimental studies water jet impact on rock and rocklike materials:Proceeding of the 3rd International Symposium on Jet Cutting Technology,Chicago,USA,1976[C].Chicago,1976.

[4] 孙清德,汪志明,王超,等.水力机械联合破岩主要配合参数的实验研究[J].石油钻采工艺,2006,28(2):7-10.SUN Qing-de,WANG Zhi-ming,WANG Chao,et al.Exper iment study on work-in parameters of combined high pressure jet and mechanical bit breaking rock[J].Oil Drilling&Production Technology,2006,28(2):7-10.

[5] 易灿,李根生,胡永堂.淹没条件下锥形喷嘴射流破岩效率实验研究[J].石油钻探技术,2001,29(1):10-12.YI Can,LI Gen-sheng,HU Yong-tang.Experiment study on rock erosion efficiency with conical nozzles under submerged condition[J].Petroleum Drilling Techniques,2001,29(1):10-12.

[6] 胡寿根,蒋彧澄.冲蚀试样性能分析及水下高围压射流试验研究[J].机械工程学报,2000,36(6):95-98.HU Shou-gen,J IANG Yu-cheng.Analysis on performance of the erosion sample and experimental study on high environmental pressure underwater jet[J].Journal of Mechanical Engineering,2000,36(6):95-98.

[7] 李根生,廖华林,黄中伟,等.超高压水射流作用下岩石损伤破碎机理[J].机械工程学报,2009,45(10):284-293.L I Gen-sheng,L IAO Hua-lin,HUANG Zhong-wei,et al.Rock damage mechanisms under ultra-high pressure water jet impact[J].Journal of Mechanical Engineering,2009,45(10):284-293.

[8] 廖华林,李根生,罗学钊,等.超高压水射流冲击应力分布规律的数值分析[J].石油钻采工艺,2004,26(5):8-12.L IAO Hua-lin,L IGen-sheng,LUO Xue-zhao,et al.Numerical analysis on the stress distribution of super high pressure water jet-flow impinging solid[J].Oil Drilling&Production Technology,2004,26(5):8-12.

[9] 孙清德,汪志明,于军泉,等.高压水射流破岩规律的数值模拟研究[J].岩土力学,2005,26(6):978-982.SUN Qing-de,WANG Zhi-ming,YU Jun-quan,et al.A disquisition on breaking mechanism of high pressure jet impacting on rock[J].Rock and Soil Mechanics,2005,26(6):978-982.

[10] NI Hongjian,WANG Ruihe.A theoretical study of rock drilling with a high pressure water jet[J].Petroleum Science,2004,1(4):72-76.

[11] 王敏生,唐波.井底应力场对气体钻井井斜的影响[J].岩土力学,2009,30(8):2436-2441.WANG Min-sheng,T ANG Bo.Effects of stress field in bottom hole on borehole deviation during gas drilling[J].Rock and Soil Mechanics,2009,30(8):2436-2441.

[12] 陈勉,金衍,张广清.石油工程岩石力学[M].北京:科学出版社,2008.

[13] 汪志明,崔海清,何光渝.流体力学[M].北京:石油工业出版社,2006.

[14] 孔祥言.高等渗流力学[M].合肥:中国科学技术大学出版社,1999.

[15] 龙芝辉,汪志明,范军,等.射流对岩石局部孔隙压力的影响[J].天然气工业,2006,26(9):77-79.LONG Zhi-hui,WANG Zhi-ming,FAN Jun,et al.Effects of jet on local pore pressure of rocks[J].Natural Gas Industry,2006,26(9):77-79.

[16] 曾攀.有限元分析及应用[M].北京:清华大学出版社,2004.

[17] 左魁,张继春,曾鲜明,等.重复爆炸条件下地冲击效应试验研究[J].岩石力学与工程学报,2007,26(1):3378-3383.ZUO Kui,ZHANG Ji-chun,ZENG Xian-ming,et al.Experimental study on underground shock effects under repeated explosions[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(1):3378-3383.

[18] 胡刚,郝传波,景海河.爆炸作用下岩石介质应力波传播规律研究[J].煤炭学报,2001,26(3):270-273.HU Gang,HAO Chuan-bo,J ING Hai-he.Study of the laws of stress wave propagation in rock bar under blasting loading[J].Journal of China Coal Society,2001,26(3):270-273.

(编辑 李志芬)

Influence of water jet impact load on bottom-hole rock stress field

CHANG De-yu,LI Gen-sheng,SHEN Zhong-hou,HUANG Zhong-wei,T IAN Shou-ceng,SHI Huai-zhong,SONG Xian-zhi

(State Key Laboratory of Petroleum Resource and Prospecting in China University of Petroleum,Beijing102249,China)

The fluid-solid coupling model of jet impacting rock,considering the four factors of three-dimensional in-situ stress,fluid column pressure,pore pressure and jet velocity,was established and calculated by the finite element method and finite volume method.The results show that the maximum principal stress of the rock increases with the increase of bottom-hole differential pressure.The maximum jet impact force is proportional to the square of the jet velocity,and the pore pressure at the impact surface and impact axis decreases in the form of cubic parabola with the increase of the distance.The local effect is obvious when the jet impacting the bottom-hole rock,the affected main district of jet is two times of jet radius at the impact surface and between 2.5 times and 3.5 times of jet radius along the impact radius,which is consistent with the stress-wave theory.

water jet;bottom-hole rock;fluid-solid coupling;stress field;finite element method;finite volume method

TE 21

A

10.3969/j.issn.1673-5005.2011.02.013

2010-11-24

国家“973”重点基础研究发展计划项目(2010CB226704)

常德玉(1984-),男(汉族),山东菏泽人,博士研究生,主要从事石油工程和高压水射流研究。

1673-5005(2011)02-0074-06