多目标灰色关联度模型在工程项目投资决策中的应用
王晓明,贺昌政
0 引言
随着市场经济的发展和投资体制的不断完善,企业投资行为逐步由国家按照行政决策程序审批下达方式转变为企业自主决策和审批。但由于企业面临环境的复杂性,很多情况难以预料,这种不确定性就大大增加了企业投资规划和决策的难度。
在投资项目管理的全过程当中,投资前期的工作至关重要,投资前期,决策环节又是关键[1]。目前,在工程项目投资决策中仍存在着一些不容忽视的问题,例如把咨询看得很重,而对评估却关心甚少,在经济和技术方面还是只看重经济,不重视技术,不重视多方案比较和论证,很多工程项目切合实际的备选方案少,即便有多个备选方案,那也只是表面而已,分析的透明度远远不够深入,依据不够充分,论证也不够具体,有的方案犹如纸上谈兵,对一些该考虑的因素也未列入其中。因此,工程类企业进行决策时,未来前景的好与坏取决于是否能有一个科学合理的决策方法的提出。
目前应用于投资决策领域的主要理论有实物期权理论、模糊数学理论和灰色系统理论等,其中灰色系统着重研究其他方法所不能解决的“小样本、贫信息不确定”问题,同时该系统能够将各个方案或各个因素之间的灰色关系定量描述。本文拟在工程项目投资决策中引入多目标灰色关联度模型,利用科学的方法进行工程项目投资决策。
1 构建工程项目投资决策的多目标灰色关联度模型的步骤
在此我们假设工程项目多目标决策问题中可用来参考的方案有n个,将其记为X={x1,x2,…,xn},有m个备选方案评价指标,记为V={v1,v2,…,vm},备选方案xi关于第 j个指标vj的指标值用 xij(i=1,2,…,n;j=1,2,…,m)表示,则 n个备选方案的n×m个指标值构成矩阵Z=(xij)n×m,称为备选方案集对指标集的评价矩阵,备选方案需要的信息都是从Z=(xij)n×m中获得[2]。
1.1 理想方案的确定
不妨设工程项目多目标决策问题的方案集合为X={x1,x2,…,xn},方案的指标集合为V={v1,v2,…,vm},把相对于理想决策方案x0对指标vj的属性值记为x0j,并且符合:当备选方案因素指标vj为经济效果型指标时,例如利润,则 x0j=max(x1j,x2j,…,xnj),当备选方案因素指标vj为消耗型指标时,例如投资回收期时,x0j=min(x1j,x2j,…,xnj),当备选方案因素指标vj为比率型指标时,例如资产负债率时,xij,称矩阵 A=(xij)(n+1)×m,(i=0,1,2,…,n);
j=(1,2,…,m)为备选方案集X相对指标集V的决策矩阵。
这里还需要考虑备选方案中涉及的多个目标问题的指标间的量纲,如果量纲不一样,指标间的量纲差异更大,为了减少量纲差异造成的影响,在投资决策分析之前需要进行指标的无量纲处理,使评价分析更加合理。用数列x的初始值x(1)除以数列x中的每一个数,得到一个新的序列。可记 INGO:x→x'。
所得到的数列无量纲,且有公共交点x(1)=1。
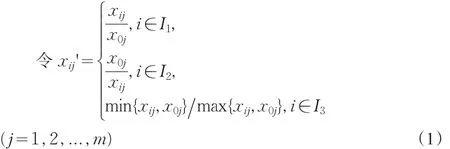
其中I1代表经济效果型;I2代表消耗型;I3代表比履型的下标集合,A'=(xij')(n+1)×m代表 A=(xij)(n+1)×m的初始化矩阵。可知,备选方案经过初值化处理以后,x0j'=1(j=1,2,…,m),x0'=(x01',x02',…x0m')=(1,1,…,1)即为工程项目投资决策的理想方案。
1.2 备选方案关联度计算公式
用向量 x0'=(x01',x02',…x0m')=(1,1,…,1)来表示工程项目决策理想方案 x0,把他作为母序列,向量xi'=(xi1',xi2',…,xim')来表示待评决策方案xi,把他当作子序列,x0'与 xi'的第 j点的数为 x0j'与 xij',x0'与 xi'在第 j点的关联系数定义为rj(xi',x0'),写为rij:
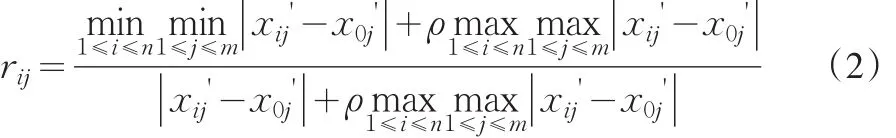
式中,ρ代表分辩率系数,ρ∈( )0,1 ,通常取 ρ=0.5。由于最大绝对数之间的差值能够导致失真,分辨率系数可以减少这种失真。
多目标灰色关联矩阵由n×m个灰色关联系数rij(i=1,2,…,n;j=1,2,…,m)构成:

关联系数表示两个被比较的序列在某一时刻的靠近程度,但关联系数不方便进行比较,因为它所提供的有效信息比较发散,由此需要计算加权关联度:
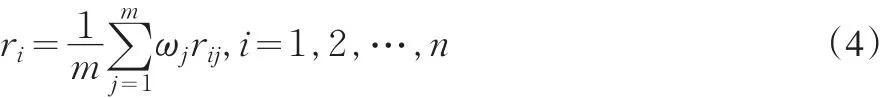
式中:ωj代表指标vj的权系数,ri代表子数列xi'与母数列x0'各个时点的所有关联系数rij的加权平均值,它表示的是关联度,也就是理想方案与备选方案之间的相近程度。
如果母数列与子数列在每个时点都能共线,也就是相关联系数是1,那么母数列与子数列的关联度肯定是1。ri值越大,说明理想方案x0与工程项目投资决策备选方案xi的值越接近,方案xi更好[3]。
1.3 指标因素权重的确定
现在学者们大多研究的是多目标决策中的目标权重问题,还很少研究用灰色关联度来确定目标权重。本文利用备选方案因素指标的灰色关联度来确定指标权重,方法如下:
首先确定母指标与子指标:母指标选择对工程项目投资决策方案影响最大的指标,其对应的指标值向量用Y0=(x10,x20,…,xn0)T表示。母指标以外的备选方案指标作为子指标,子指标所对应的指标值向量用Yj=(x1j,x2j,…,xnj)T,(j=1,2,…,m)表示。
对Y0和Yj的初始化处理:
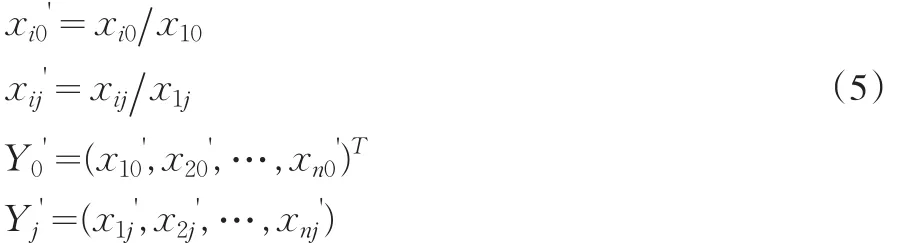
得初始化指标值矩阵B=(Y0',Yj')。
然后计算Yj和Y0关联系数为:
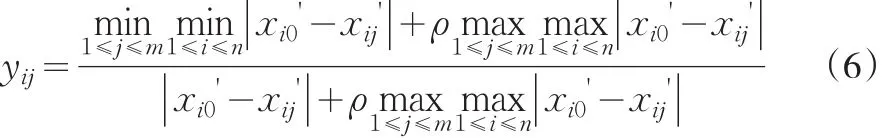
得关联系数矩阵
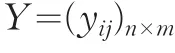
对矩阵Y=(yij)n×m的列求平均数,得:
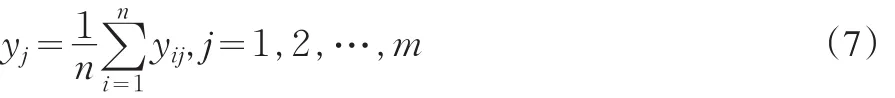
(7)式代表第 j个指标与母指标的关联程度,如果yj越大,表示第 j个指标与母指标越靠近,即备选评价方案或者是经济效益的影响程度也就越大。令:
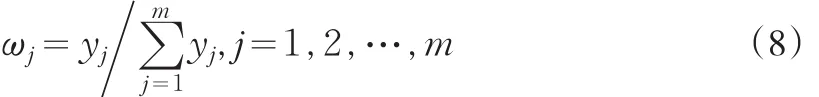
可将W=(ω1,ω2,…,ωm)作为指标的权重。
x0(理想方案)相对xi(工程项目投资决策方案)的加权灰色关联度为:
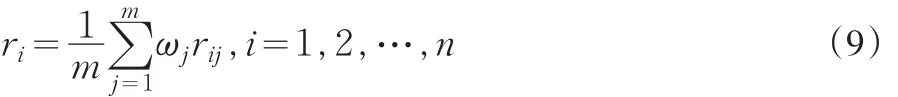
2 工程项目投资决策中多目标灰色关联度决策模型的构建
通过进行系统的研究,可以得出方案的灰色关联矩阵是:
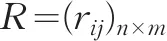
W=(ω1,ω2,…,ωm)表示m个因素指标的总目标权重向量。
r=(r1,r2,…,rn)表示xi的加权灰色关联度构成的灰关联向量,其中xi是每个相对理想方案x0的工程项目决策方案。
评价方案好坏的原则采用加权灰色关联度的理论,并运用多目标灰色关联理论:
(1)如果ri的值越大,方案xi越可行。因为ri的值越大,工程项目投资决策备选方案xi和理想方案x0的值就越接近。
(2)如果ri=max(r1,r2,…,rm),那么 xi就是我们要找的工程项目投资决策所有方案中的最优方案。
(3)ri按大小排列的顺序,就是工程项目投资决策备选方案的排列顺序[4]。
由此,就可以将多目标灰色关联度模型应用到现实中的工程投资决策的问题中来,为决策者提供决策的依据[5]。
3 应用实例
3.1 项目概况
某能源有限公司新启动一项油田开发项目,投资总额共80亿元,现根据项目概况制定出四种油田开发方案,为了便于计算,每一种方案只选取了八项指标,指标分别为:①采气速度;②投资回收期;③采出程度;④产气量;⑤内部收益率;⑥利润;⑦成本;⑧净现值率。每个指标的数据情况如表1所示,试图通过各个项的指标予以分析评价,找出此项目投资决策的最佳方案。
3.2 模型应用
应用基于灰色关联理论建立的工程项目投资决策模型,来讨论石油工程项目的最优方案。
因素指标的关联度yj:
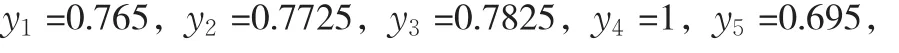
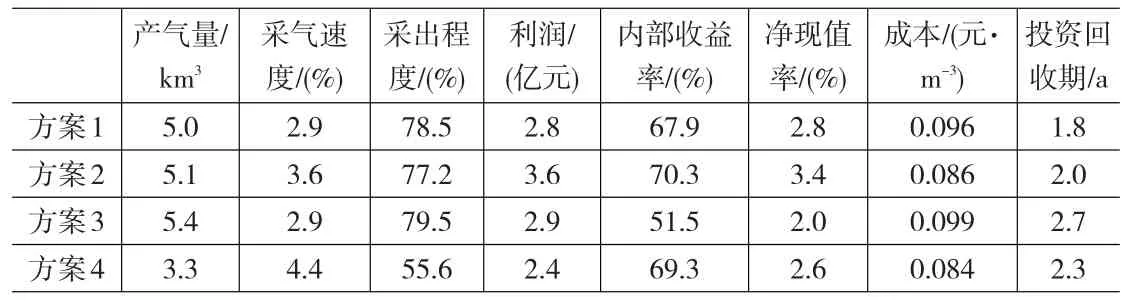
表1 某油田工程开发方案
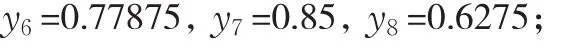
因素指标的权重W=(ω1,ω2,…,ωm):
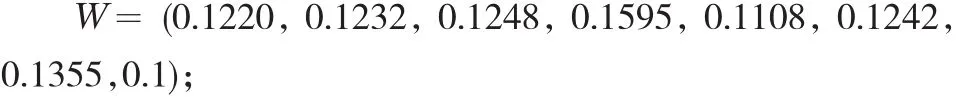
石油工程项目开发方案的加权灰色关联度向量r:
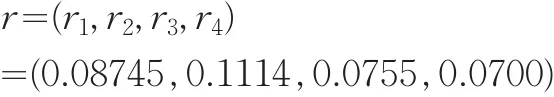
由于r4<r3<r1<r2,可得到石油工程项目开发方案的排名次序从低到高是:4,3,1,2,石油工程项目开发方案中最优的开放方案显而易见是第2个方案。
4 结论
(1)工程项目投资决策系统属于灰色系统,引入灰色关联理论解决其投资决策问题,使工程项目投资决策更具科学性。
(2)以工程项目投资决策为背景的多目标灰色关联度模型,有规范的构建步骤,即:首先是决策矩阵以及它的初始化,其次是方案的关联度计算,再次是确定因素指标权重。
(3)针对石油工程项目的投资决策问题,建立了多目标灰色关联度模型,这一模型的建立是由于工程项目的不确定性及多目标性。该模型的有效性也得到了验证。
[1]陈玲丽,陈一君,林映光.基于模糊理论的石油工程项目投资决策优化研究[J].四川理工学院学报(自然科学版),2009,(3).
[2]亢玉晓,杨先豪.基于灰色关联度的混合型多属性决策问题[J].湖南工程学院学报(自然科学版),2011,(1).
[3]孙红霞.基于灰色关联度的模糊层次组合交通安全评价模型[J].交通与运输(学术版),2011,(1).
[4]李秀红.基于灰色关联度的多目标决策模型与应用[J].山东大学学报(理学版),2007,(12).
[5]张玉清.多目标灰色关联度决策模型分析[J].中国环境管理干部学院学报,2008,13(4).

