一类区间线性双层规划的最小最大后悔解及其解法

王建忠，杜 纲

0 引言

双层规划由于其广泛的实际背景而成为近年来一个重要研究主题，在理论和算法方面都取得了一系列的成果。这些成果主要是针对确定性的问题，但现实中许多递阶决策问题具有一定的不确定性。在各种不确定性的类型中，具有区间系数的规划问题是最基本和重要的一种。这不仅因为其在实际应用中最为简单和常用，而且其他不确定性的类型如含有模糊系数和随机系数的情形[1]往往要化为区间系数的情形来处理。因此，研究具有区间系数的双层规划问题具有十分重要的意义。

目前，对于区间双层规划的研究还很少。本文将最小最大后悔原则方法[2～6]推广到区间线性双层规划，提出了基于遗传算法的求解方法，最后通过算例说明了方法的可行性和有效性。

1 区间线性双层规划

本文考虑如下形式的区间双层线性规划：

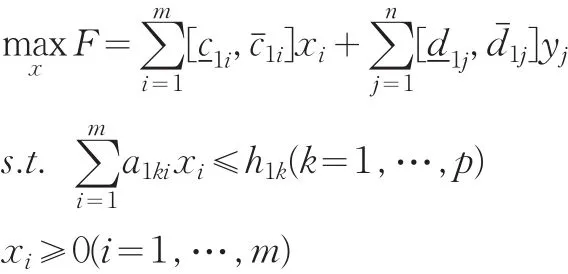
y是下面规划的解: （1）

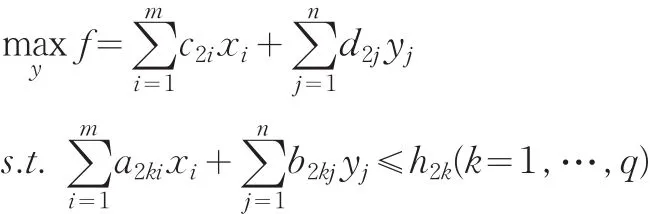
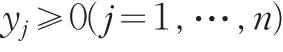
模型(1)的矩阵向量形式分别为：

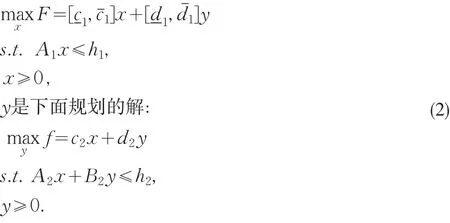
对区间线性双层规划(1)作如下说明：

(1)对Min F型可通过Max-F变为以上形式；

(2)对≥型的约束，可通过两边同乘－1变为≤型的约束；

(3)若某个 xi≤0，通过变换 x'i=-xi，有 x'i≥0；yj≤0可作同样处理；

(4)若某个 xi或 yj是自由变量，一般不通过变换将其转化为大于零的变量。因为在各种处理区间线性双层规划的方法中，可能会导致和x'i的系数不同，使变换失去意义。

(5)对于自由变量 xi，可分别讨论 xi≤0和 xi≥0的情形，然后根据决策问题的需要以及区间处理方法的选择来进一步分析。

(6)模型中仅涉及不等式约束。因为等式是一种严格的数量关系要求，区间等式在实际应用中比较少见，而且一般将其转化为各种形式的不等式约束来解释相等关系。

2 最小最大后悔解的定义及性质

定义1区间线性双层规划(2)的约束域：

Ω={(x,y)|A1x≤h1,A2x+B2y≤h2,x≥0,y≥0}

约束域Ω在上层决策空间的投影：

S={x|∃y,A1x≤h1,A2x+B2y≤h2,x≥0,y≥0}；

对于x∈S，下层规划的合理反应集：

M(x)={y|y∈argmax{c2x+d2y,B2y≤h2-A2x,y≥0}}；

区间线性双层规划(2)的诱导域：

IR={(x,y)|(x,y)∈Ω,y∈M(x)}。

假设1约束域Ω非空且为紧集。

假设2对任意x∈S，下层规划有唯一最优解。

定义2给定c1∈[-c1,cˉ1]，d1∈[-d1,dˉ1]，称OS(c1,d1)={(x',y')∈IR|c1x'+d1y'=为区间线性双层规划在c1,d1下的最优解集。

取定c1,d1后，区间线性双层规划（2）即转化为确定型双层规划。根据定义3可知，对于(x,y)∈CS，无论系数c1,d1如何取值，(x,y)都是c1,d1取定后的确定型线性双层规划的最优解。

根据定义4可知，对于 (x,y)∈PS，必然存在c1∈[-c1,cˉ1]，d1∈[-d1,dˉ1]使得 (x,y)为 c1,d1取定后的线性双层规划的最优解。

显然，完全最优解是区间线性双层规划(2)最为理想的解定义，但很多情况下，完全最优解并不存在。下面引入后悔度及最小最大后悔度解的定义。

假设以某个(x*,y*)∈IR为区间线性双层规划(2)的解，而在此决策后，上层决策者知道目标函数中的区间系数的真正取值为c*1,d1*。1,d*1下的后悔度。

然而，在现实决策前，不可能猜到区间系数的真正取值，故

定义6称R(x*,y*)=y*)]为 (x*,y*)在 c*定义5称(c1, d 1,x*,y*) 为(x*,y*)∈IR的最大后悔度。

根据定义5、6和7，区间线性双层规划(2)的最小最大后悔解可通过问题(3)求解：

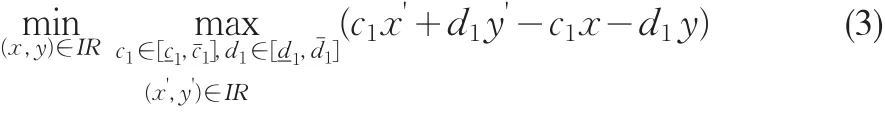
定理1在假设条件1和2下，区间线性双层规划(2)必然存在最小最大后悔解。

证明：由假设条件1和2下，IR非空，故对于任意给定的 c1∈[-c1,cˉ1],d1∈[1,1]，(2)均有最优解。根据定义7可知，区间线性双层规划(2)必然存在最小最大后悔解。证毕。

定理2若(x*,y*)是区间线性双层规划(2)的最小最大后悔解，且最大后悔值R(x*,y*)=0，则(x*,y*)为(2)的一个完全最优解。

证明：假设(x*,y*)不是区间线性双层规划(2)的一个完全最优解，即存在 c1'∈[c-1,cˉ1],d1'∈[-d1,dˉ1]和 (x',y')≠(x*,y*)使得(x',y')是取c1=c1'，d1=d1'后线性双层规划(2)的最优解，则有 c1'x'+d1'y'＞c1'x*-d1'y*。根据最大后悔度的定义，d'1y*＞0，与R(x*,y*)=0矛盾。故(x*,y*)(2)的一个完全最优解。证毕。

定理3(4)的最优解为区间线性双层规划(2)的最小最大后悔解。

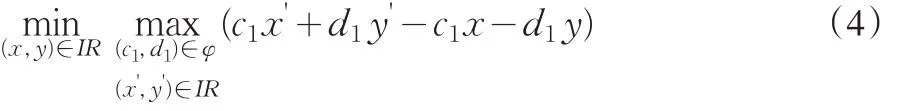
其中，φ ={(c11,…,c1m,d11,…,d1n)|c1i=cˉ1i或-c1i,d1j=dˉ1j或-d1j,i=1,…,m,j=1,…,n}。

证明：任意给定(x*,y*)∈IR，考虑(3)式的内层规划问题(5):

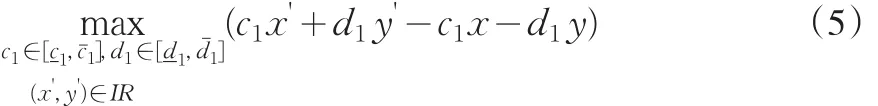
设(5)的最优解为 c*1∈[-c1,cˉ1],d*1∈[-d1,dˉ1],(xˉ,yˉ)。

3 基于遗传算法的最小最大后悔解求解

具有区间系数的规划问题的最小最大后悔解的求解比较复杂，即便是最简单的区间线性规划。Averbakh和Lebedev证明了基于最小最大后悔度的区间系数目标函数的线性规划的计算复杂性是NP-Hard的。遗传算法是一种通过模拟自然进化过程搜索最优解的方法，具有较好的全局收敛性。本文采用实数编码的遗传算法求解区间线性双层规划的最小最大后悔解，具体设计如下：

（1）个体表达：个体(x,y)采用实数编码，每个个体中y的取值通过单纯形法计算(2)的下层规划求得。

（2）适应度函数： Fit(x[r],y[r])=M-+d1y-c1x[r]-d1y[r])，其中，M为较大的数；ψ中的每个元素由(c1,d1)∈φ及其对应的线性双层规划的最优解(x,y)组成。

（3）选择策略：采用转盘赌选择法和精英保留法组合的方法。

（4）交叉策略：采用自适应算术交叉,其中交叉概率随个体的适应度大小变化，交叉概率

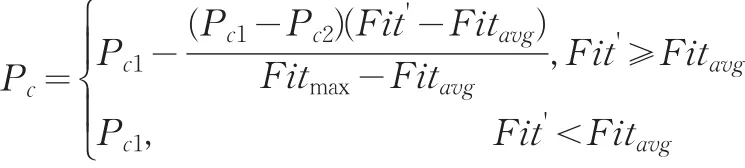
式中，fmax为最大适应度值，favg为当代群体中的平均适应度值，Fit'为要交叉的两个个体中较大的适应度值。设交叉的个体为 x[r1]和 x[r2]，则后代中的分别为将代入(2)求下层规划得到的相应的解，其中β为[-0.2,1.2]上的随机数。若交叉后代不可行，则重新生成随机数β，重新进行交叉。

（5）变异策略：采用自适应随机变异，其中变异概率随变异个体的适应度大小变化，变异概率

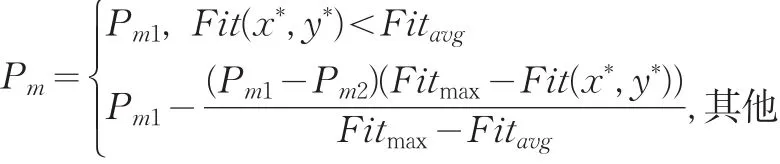
设x*为变异个体，在[0,1]上生成随机数β2和β3，

在[1,m]上生成一个随机整数k，β2≥0.5，令x'

i=x*i,i=1…,k-1,k+1,…,m,x'k=x*k+ β3(xˉk-x*k)；否 则 ，令x'i=x*i,i=1…,k-1,k+1,…,m,x'k=x*k-β3(x*k-)，其中 xˉk和为(6)和(7)的解，y'为将 x'代入(2)求下层规划得到的相应的解。

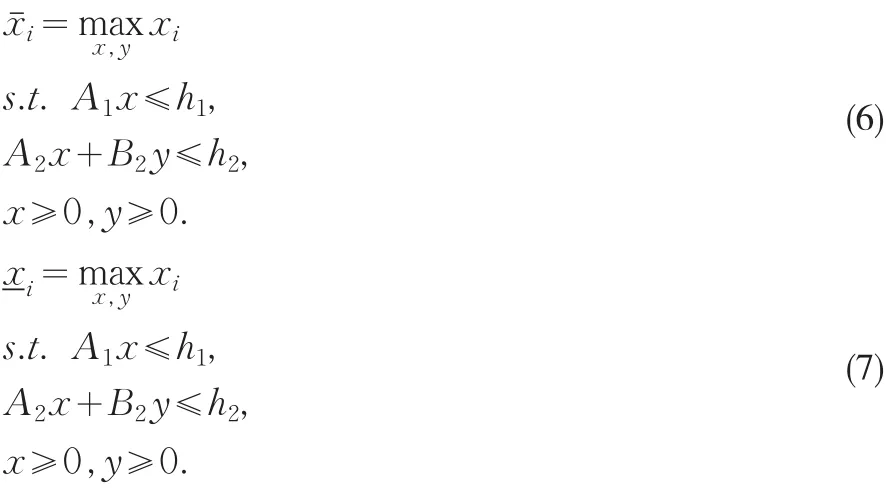
若变异后代(x',y')不可行，则重新进行变异。

4 算例

考虑如下区间线性双层规划：

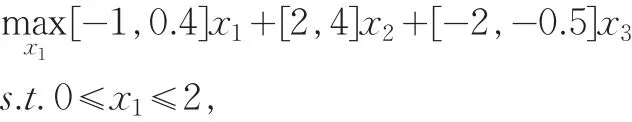
x2,x3是如下规划的解

首先，计算(c1,d1)∈φ时，各种系数组合下(8)的最优解，如表1所示：

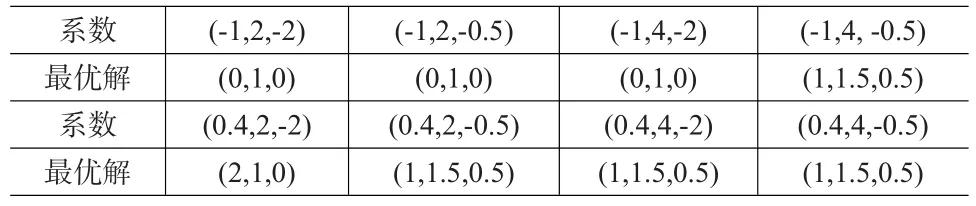
表1 不同系数取值下的最优解

采用遗传算法对其求解,设置种群规模为20，交叉概率参数 Pc1=0.4，Pc2=0.1，变异概率参数 Pm1=0.1，Pm2=0.05，最大迭代次数为500。通过Matlab R2008a计算得最小最大后悔解为（1,1.5,0.5）,即当上层决策者选择x=1为决策时，最大后悔度最小，最大后悔度的值为1。

5 结语

具有区间系数的双层规划是一类重要的不确定递阶决策问题。针对上层目标函数具有区间系数的区间线性双层规划，提出了最小最大后悔解的概念，并讨论了其与可能最优解和完全最优解的关系，根据最小最大后悔解的特点设计了基于遗传算法的求解方法。数值算例验证了算法的有效性和可行性。

[1]彭锦,刘宝碇.不确定规划的研究现状及其发展前景.运筹与管理,2002,11(2).

[2]Shimizu K,Aiyoshi E.Necessary Conditions for Min-max Problems and Algorithms by a Relaxation Procedure[J].IEEE Transactions on Automatic Control,1980,（25）.

[3]Inuiguchi M,Sakawa M.Maximum Regret Analysis in Linear Programs with an Interval Objective Function[C].In Proceedings of IWSCI’96,1996.

[4]Mausser H E,Laguna M.A.New Mixed Integer Formulation for the Maximum Regret Problem[C].Working Paper,Graduate School of Business,University of Colorado,Boulder,CO,1997.

[5]Kouvelis P,Yu G.Robust Discrete Optimization and Its Applications[M].Boston:Kluwer Academic Publishers,1997.

[6]Mausser H E,Laguna M.A Heuristic to Minimax Absolute Regret for Linear Programs with Interval Objectives Function Coefficients[J].European Journal of Operational Research,1999,117(1).