集值转移测度的JL收敛的等价条件

赵冬霞

(大庆师范学院 数学科学学院,黑龙江 大庆 163712)

1 引言与预备

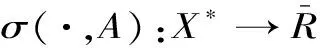
设(X,J)为任意拓扑空间,记P(X)为X的幂集,对于任意B∈P(X)记I*(B)={A∈P0(X),A⊂B},I*(B)={A∈P0(X),A∩B≠Ω},J*={I*(G),G∈J}，J*={I*(G),G∈J}。[2]

定义 1[2]：设(Ω,A)为一可测空间，M:A→P0(X)为集值函数,M(Ø)={0},称M为集值测度,如果对任意不交集列{An,n≥1}⊂A有

定义2[4]：(线形拓扑)设X为Banach空间,任给非零的x*∈X*,α∈R记

称Pfc(X)以{I*(G),H(x*,α),G⊆X}为强开集，x*∈X*非零，α∈R为子基的拓扑为形拓扑,为了研究线形拓扑的性质,我们需要下面容易证明的引理1，任给非零x*∈X*,α∈R，记L(x*,α)={x∈X,},任给

A,B∈Pfc(X),D(AB)=inf{‖a,b‖,a∈A,b∈B}

为A,B间的分离度,显然我们有,A∩B≠Ω当且仅当D(A,B)=0。

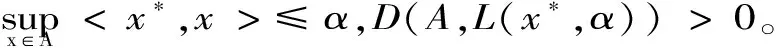
D(A,L(x*,α))=sup{ε,(A+ε)∩L(x*,α)=Ø}

证明见文献2的引理1.3.4。

定义3[2]：设(Ω,A)，(T,B)为可测空间,X是Banach空间，称M:Ω×B→Pf(X)为集值转移测度，如果它满足：

1) 任给A∈B,M(·,A)关于ω∈Ω可测；

2) 任给ω∈Ω,M(ω,·)为(T,B)上的集值测度。

称m:Ω×B→X为M(·，·)选择转移测度，如果它满足：

1) 任给A∈B,m(·,A)关于ω∈Ω可测；

2) 任给ω∈Ω,m(ω,·)为(T,B)上的可数可加向量测度；

3) 任给ω∈Ω,A∈B,m(ω,A)∈(ω,A)。

集值转移测度M(·,·)的选择转移测度全体记作TSM。

2 主要结果

以下不做特别说明,设(Ω,A),(T,B)为一可测空间, {Mn,n≥1}为Pf(X)值集值测度序列,M:A→Pf(X)为集值测度，任给ω∈Ω,M(ω,·)为(T,B)上的集值测度。

定义4： {M(ω,·),Mn(ω,·),n≥1}⊂Pf(X)

定理1：设{M(ω,·),Mn(ω,·),n≥1}⊂Pfc(X)则下列命题等价

1) (JL)Mn(ω,·)→M(ω,·)。

2) {Mn(ω,·)}在线形拓扑下(Pfc(X),JL)意义下收敛到M(ω,·)。

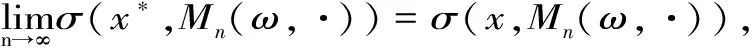
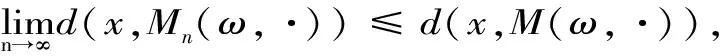
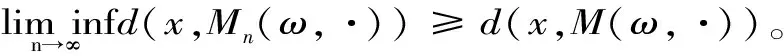
混凝土充灌完成后，应同时进行护面混凝土的清洗、养护。一般养护期为7天，要求在此期间护坡表面处于润湿状态。

即(wijs)Mn(ω,·)→M(ω,·)。其次,我们证明(w)Mn(ω,·)→M(ω,·),若x*∈X*为零元素,σ(x*,M(ω,·)),σ(x*,Mn(ω,·))(n≥1)为零。不妨设x*∈X*非零，令α=σ(x*,M(ω,·)),对于任给ε>0,由于M(ω,·)∈H(x*,α+ε),因此,存在N≥1，使得n≥N时Mn(ω,·)∈H(x*,α+ε)，即

σ(x*,Mn(ω,·))≤σ(x*,M(ω,·))+ε

依ε>0的任意性可得

另一面,任给ε>0依支撑函数的定义必存在x∈M(ω,·),使得>α-ε由于

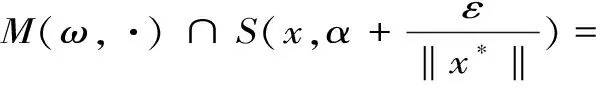
因此存在N≥1使得n≥N时，

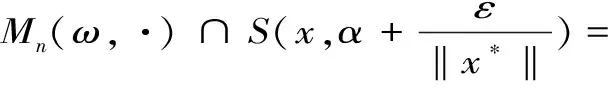
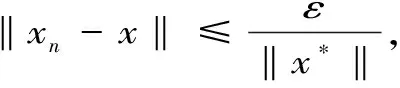
σ(x*,Mn(ω,·))≥

=-

≥-‖x*‖·‖x-xn‖

>-ε>α-2ε

依ε>0的任意性可知

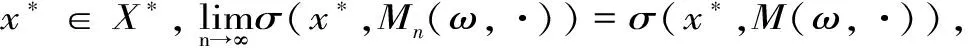
3 结语

综上所述，在给出集值转移测度定义的条件下，我们研究了集值转移测度JL收敛的等价条件，即设在{M(ω,·),Mn(ω,·),n≥1}⊂Pjc(X)条件下，(JL)Mn(ω,·)→M(ω,·) 等价于{Mn(ω,·)}，在线形拓扑下(Pjc(X),JL)意义下收敛到M(ω,·) ，这使我们从线形拓扑的角度来研究集值转移测度的收敛性具有一定的意义。

[参考文献]

[1] 中山大学测度与概率基础编写组. 测度与概率基础[M].广州：广东科技出版社,1984：260-267.

[2] 张文修,汪振鹏,高勇. 集值随机过程[M].北京：科学出版社,1996：58-81.

[3] 张恭庆,林源渠.泛函分析讲义[M].北京：北京大学出版社,1987：56-79.

[4] 熊金城. 点集拓扑讲义[M].北京：高等教育出版社,1998：78-80.

[5] 张玲,徐明跃,王涛.集值测度的收敛性及其与Castaing向量表示中测度的收敛性之间的关系[J].数学杂志，2009,29(6):769-773.